贝叶斯公式由浅入深大讲解—AI基础算法入门
2018-04-20 19:58
645 查看
1 贝叶斯方法
长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。而且概率虽然未知,但最起码是一个确定的值。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,而且不论你取了多少次,取得白球的概率θ始终都是1/2,即不随观察结果X 的变化而变化。 这种频率派的观点长期统治着人们的观念,但是:
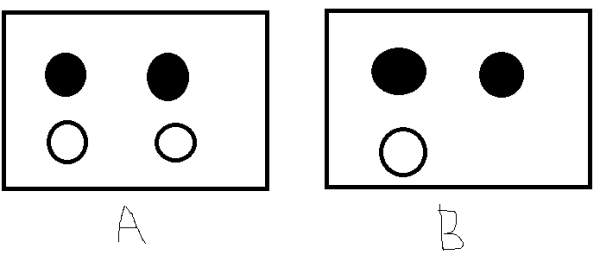
假设我们有如下的7个球在A,B两个框中,如果我们随便取一个球,已知取到的球来自B框中,那么这个球是白球的概率是多少呢?或者问去除的球是白色,那么取自B框的概率是多少呢?这个问题不是很好解决,直到后来一个名叫Thomas Bayes的人物出现。1.1 贝叶斯方法的提出 托马斯·贝叶斯Thomas Bayes(1702-1763)在世时,并不为当时的人们所熟知,很少发表论文或出版著作,与当时学术界的人沟通交流也很少,用现在的话来说,贝叶斯就是活生生一民间学术“屌丝”,可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”,翻译过来则是:机遇理论中一个问题的解。你可能觉得我要说:这篇论文的发表随机产生轰动效应,从而奠定贝叶斯在学术史上的地位。
事实上,上篇论文发表后,在当时并未产生多少影响,在20世纪后,这篇论文才逐渐被人们所重视。对此,与梵高何其类似,画的画生前一文不值,死后价值连城。 回到上面的例子:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率θ是多少?”贝叶斯认为取得白球的概率是个不确定的值,因为其中含有机遇的成分。比如,一个朋友创业,你明明知道创业的结果就两种,即要么成功要么失败,但你依然会忍不住去估计他创业成功的几率有多大?你如果对他为人比较了解,而且有方法、思路清晰、有毅力、且能团结周围的人,你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式,便是贝叶斯式的思考方式。 继续深入讲解贝叶斯方法之前,先简单总结下频率派与贝叶斯派各自不同的思考方式:
频率派把需要推断的参数θ看做是固定的未知常数,即概率θ虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
而贝叶斯派的观点则截然相反,他们认为参数θ是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数θ的分布。
相对来说,频率派的观点容易理解,所以下文重点阐述贝叶斯派的观点。 贝叶斯派既然把θ看做是一个随机变量,所以要计算θ的分布,便得事先知道θ的无条件分布,即在有样本之前(或观察到X之前),θ有着怎样的分布呢? 比如往台球桌上扔一个球,这个球落会落在何处呢?如果是不偏不倚的把球抛出去,那么此球落在台球桌上的任一位置都有着相同的机会,即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为先验分布,或的无条件分布。 至此,贝叶斯及贝叶斯派提出了一个思考问题的固定模式: 先验分布 π(θ)+ 样本信息χ⇒ 后验分布π(θ|x)上述思考模式意味着,新观察到的样本信息将修正人们以前对事物的认知。换言之,在得到新的样本信息之前,人们对的认知是先验分布 π(θ),在得到新的样本信息后χ,人们对θ的认知为π(θ|x)。而后验分布π(θ|x)一般也认为是在给定样本χ的情况下θ的条件分布,而使达到最大的值称为最大后θMD验估计,类似于经典统计学中的极大似然估计。 综合起来看,则好比是人类刚开始时对大自然只有少得可怜的先验知识,但随着不断是观察、实验获得更多的样本、结果,使得人们对自然界的规律摸得越来越透彻。所以,贝叶斯方法既符合人们日常生活的思考方式,也符合人们认识自然的规律,经过不断的发展,最终占据统计学领域的半壁江山,与经典统计学分庭抗礼。 此外,贝叶斯除了提出上述思考模式之外,还特别提出了举世闻名的贝叶斯定理。1.2 贝叶斯定理 在引出贝叶斯定理之前,先学习几个定义:边缘概率(又称先验概率):某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
联合概率表示两个事件共同发生的概率。A与B的联合概率表示为P(A∩B)或者P(A,B)。
条件概率(又称[b]后验概率)[/b]:事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”,。
接着,考虑一个问题:P(A|B)是在B发生的情况下A发生的可能性。首先,事件B发生之前,我们对事件A的发生有一个基本的概率判断,称为A的先验概率,用P(A)表示;
其次,事件B发生之后,我们对事件A的发生概率重新评估,称为A的后验概率,用P(A|B)表示;
类似的,事件A发生之前,我们对事件B的发生有一个基本的概率判断,称为B的先验概率,用P(B)表示;
同样,事件A发生之后,我们对事件B的发生概率重新评估,称为B的后验概率,用P(B|A)表示。
贝叶斯定理便是基于下述贝叶斯公式:
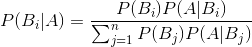
P(A|B)=P(B|A)P(A)/P(B)上述公式的推导其实非常简单,就是从条件概率推出。 根据条件概率的定义,在事件B发生的条件下事件A发生的概率是P(A|B)=P(A∩B)/P(B)同样地,在事件A发生的条件下事件B发生的概率P(B|A)=P(A∩B)/P(A)整理与合并上述两个方程式,便可以得到:P(A|B)P(B)=P(A∩B)=P(B|A)P(A) 接着,上式两边同除以P(B),若P(B)是非零的,我们便可以得到贝叶斯定理的公式表达式:P(A|B)=P(B|A)*P(A)/P(B)
笔者在看《从贝叶斯方法谈到贝叶斯网络》的时候,看到这里,其实已经晕晕的了。P(A|B) 和 P(B|A) 之类的经常让人混淆,@待字闺中的陈老师给出了理解的一个关键点,区分出规律和现象,就是将A看成“规律”,B看成“现象”,那么贝叶斯公式看成:

陈老师在《这的理解贝叶斯公式吗》和《又一个生活中的贝叶斯应用》给出了几个通俗易懂的例子,这里不再赘述。贝叶斯推断的含义
然后搜下,发现其实还有更好阐释,比如对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。所以,条件概率可以理解成下面的式子:后验概率 = 先验概率 x 调整因子这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
贝叶斯定理应用示例:

已知某种疾病的发病率是0.001,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?假定A事件表示得病,那么P(A)为0.001。这就是"先验概率",即没有做试验之前,我们预计的发病率。再假定B事件表示阳性,那么要计算的就是P(A|B)。这就是"后验概率",即做了试验以后,对发病率的估计。根据条件概率公式,
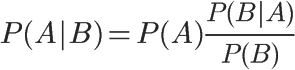
用全概率公式改写分母,
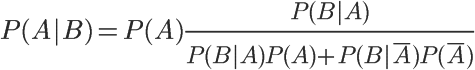
将数字代入,
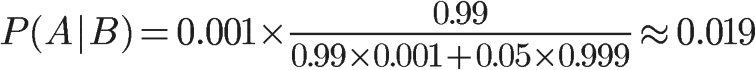
我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的"假阳性",即阳性结果完全不足以说明病人得病。或许换成这个公式 P(A|B)=P(A∩B)/B,看起来更加直白写:阐释:如果没有误报,那么得病率:.001*.99如果是误报,那么得病率为:.05*(1-.0001),所以:p(A|B)=.001*.99/[.99*.001+.05*(1-.0001)]=.019为什么会这样?为什么这种检验的准确率高达99%,但是可信度却不到2%?答案是与它的误报率太高有关。(【习题】如果误报率从5%降为1%,请问病人得病的概率会变成多少?)有兴趣的朋友,还可以算一下"假阴性"问题,即检验结果为阴性,但是病人确实得病的概率有多大。然后问自己,"假阳性"和"假阴性",哪一个才是医学检验的主要风险?
再来一个类似案例:https://www.zhihu.com/question/21134457/answer/169523403一种×××,得了这个×××的人被检测出为阳性的几率为90%,未得这种×××的人被检测出阴性的几率为90%,而人群中得这种×××的几率为1%,一个人被检测出阳性,问这个人得×××的几率为多少? 猛地一看,被检查出阳性,而且得×××的话阳性的概率是90%,那想必这个人应该是难以幸免了。那我们接下来就算算看。我们用 A 表示事件 “测出为阳性”, 用 B1 表示“得×××”, B2表示“未得×××”。根据题目,我们知道如下信息:P(B1)=.01P(B2)=.99P(A|B1)=.9P(A|B2)=.1那么我们现在想得到的是阳性的情况下,得×××的几率 P(B1,A)=P(B1)*P(A|B1)=.01*.09=0.009;
这里P(B1,A)表示的是联合概率,得×××且检测出阳性的概率是人群中得×××的概率乘上得×××时测出是阳性的几率,是0.009。同理可得得×××且检测出阳性的概率:
P(B2,A)=P(B2)*P(A|B2)=.99*.1=.099;这个概率是什么意思呢?其实是指如果人群中有1000个人,检测出阳性并且得×××的人有9个,检测出阳性但未得×××的人有99个。可以看出,检测出阳性并不可怕,不得×××的是绝大多数的,这跟我们一开始的直觉判断是不同的!可直到现在,我们并没有得到所谓的“在检测出阳性的前提下得×××的 概率 ”,怎么得到呢?很简单,就是看被测出为阳性的这108(9+99)人里,9人和99人分别占的比例就是我们要的,也就是说我们只需要添加一个归一化因子(normalization)就可以了。所以阳性得×××的概率 P(B1|A)= .009/(.099+.009)≈.083, 阳性未得×××的概率 P(B2|A)= .099/(.099+.009)≈.917 。 这里 P(B1|A),P(B2|A)中间多了这一竖线

成为了条件概率,而这个概率就是贝叶斯统计中的 后验概率!而人群中患×××与否的概率 P(B1),P(B2) 就是 先验概率!我们知道了先验概率,根据观测值(observation),也可称为test evidence:是否为阳性,来判断得×××的后验概率,这就是基本的贝叶斯思想,我们现在就能得出本题的后验概率的公式为:
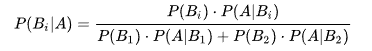
由此就能得到如下的贝叶斯公式的一般形式。我们把上面例题中的 A 变成样本(sample) x , 把 B 变成参数(parameter) \theta , 我们便得到我们的贝叶斯公式: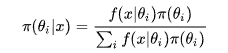
可以看出上面这个例子中,B 事件的分布是离散的,所以在分母用的是求和符号 Σ 。那如果我们的参数θ的分布是连续的呢?没错,那就要用积分,于是我们终于得到了真正的 贝叶斯公式 :
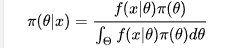
其中π指的是参数的概率分布,π(θ)指的是先验概率,π(θ|x)指的是后验概率, 指的是我们观测到的样本的分布,也就是似然函数(likelihood),记住竖线 | 左边的才是我们需要的。其中积分求的区间Θ指的是参数 θ 所有可能取到的值的域,所以可以看出后验概率π(θ|x) 是在知道 X的前提下在 Θ域内的一个关于 θ 的概率密度分布,每一个θ都有一个对应的可能性(也就是概率)。
作者:徐炎琨链接:https://www.zhihu.com/question/21134457/answer/169523403来源:知乎著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。一个更好理解的例子:链接:https://www.zhihu.com/question/51448623/answer/175907274假设你是一个领导者,或者说,山寨的头目好了。你是远近闻名的土匪头子。哈哈听闻最近官兵换统领了,可能要来剿匪了。这里驻扎的军兵每5年都会换一届统领,新官上任三把火,都想拿你们来开刀。不过每次,你都带领兄弟们打退了官兵的围剿。这次不同了,听说换的是个厉害的角色。因此,你让二头领派人下山去打探消息,看看是不是要来攻山。打探的人回来了,支支吾吾地说:官兵不会来,因为新来统领他妈生病了,回家探病去了。你这个时候,信不信他的话?你看这个回报的人,变毛变色的,说话吞吞吐吐。但是,他也有可能是因为没见过你大头领,回话的时候,有些紧张害怕。你作为一个受过高等教育的人(学过概率论,贝叶斯定理的人),心理开始盘算:1. 官兵每5年来一次,那么今年来的概率就是1/5=20%2. 派出去打探的这小子,说官兵不会来,那么今年来的概率是:03. 嗯?派出去这小子,是不是可靠,不会说的是假话吧?于是,你向旁人了解了一下:1. 三头领劝你好好考虑下,说这个小子虽然人机灵,但是经常是十句话里面有七八句是假的,嘴里没实话。于是你心理又开始盘算:1. 十之七八都假话?能吗?2.姑且认为三当家的话是真的。3.那么派出去这小子,说假话的概率就是 70%~80%:就按75%算把,说真话的概率就是25%4.那么如果他说的真话:他说官兵不来,官兵就不来的概率是:25%*80%=20% 他说官兵来 , 官兵就来的概率是 :25%*20%=5%5. 如果他说的假话:他说官兵不来,官兵 来的概率是:75%*20%=15% 他说官兵来 ,官兵不来的概率是:75%*80%=60%6. 那么他这次口口声声说了:官兵不来那么根据5.的结果:官兵来的概率是 15%官兵不来的概率是 20%比率是: 来/不来=15/20=3/4也就是说,来的概率是3/7 =42.86% 不来的概率是4/7=57.14%【注意】:贝叶斯定律是直接将 15%+20%做分母,两个概率做分子,分别重新计算其条件概率。对你一个决策者来说,这样的比率,太高,显然没有什么意义:于是你决定再派一个自己的亲信兄弟下去打探:三天后回来,回报结果还和刚才结果一样:官兵不会来,统领回家了。这次是你的亲信。应该将概率一下子修正为:官兵来:0 官兵不来 100%但是,这个亲信,虽然忠诚,明显不够机灵。他在打探时,可能被欺骗。他虽然不会骗你,但难保他被别人骗。因此,他的话只能做参考,也不可完全相信:0.参照之前那个兄弟的结果:3/7来,4/7不来1.考虑你的亲信被欺骗的概率为 30%2.那么同样:他被骗:他说官兵不来,官兵不来的概率是:3/7*30%=12.86%(实际官兵会来) 他说官兵来, 官兵来的概率是 :4/7*30%=17.14%他没被骗:他说官兵不来,官兵不来的概率是:4/7*70%=40%(实际官兵不会来)他说官兵来, 官兵来的概率是 :3/7*70%=30%3. 于是他向你报告官兵不来,那么:来/不来=12.86/40于是官兵来的概率就是12.86/(12.86+40)=20.46%看到20.46%?这个概率还是太大,你还是不放心,决定带上二当家,自己亲自下山一趟。于是你门分头走街串巷,茶馆酒肆里转悠,四处打探。最后,还是得出相同的结果。于是你将结果修正为:官兵来的概率:0,不来的概率:100%最后你和二当家在一家酒馆碰头:你说,官兵不来二当家说:我看不一定,我摸到了官兵驻扎的地方,看到了官兵在演习调动。听了这个消息,你大惊失色。你感觉自己可能也被骗了,但是凭自己的经验,被骗的可能性很小只有5%的可能性。于是,你和二当家,约定今晚,趁着月色又摸来了一趟军营。发现确实在调动军队。你心里想:我的乖乖,幸亏过来看了看,否则都没准备,就被官兵包饺子了。你一下子,又将概率修正为:官兵来:100%,官兵不来:0仔细观察了一下动静,听了听。军营里有人小声说话,你和二当家趴在外面听:士兵甲:哎?老四,你知道这回咱们要调哪里去?士兵乙:那我哪里知道,那是上头的事情。士兵甲:嘿!我劝你,把你那点银子趁早寄回家去吧。再晚,怕是没机会了。士兵乙:老三,你瞎说啥,你知道啥,又要打清风寨?士兵甲:嘿,打啥清风寨啊。要打打仗了。你心里想,不打你们山寨?打什么打仗?最近有啥大事?于是你又将那个心理的概率修正为:官兵来:0%,官兵不来:100%这个时候,你突然意识到,自己的思维好像不太对。这后面几次,信息全是压倒性的修正,一次一次,不是0%就是100%,完全不像一个受过高等教育的山寨头领。于是,你默默地多计算了两步。假设这个士兵说真话的概率为50%,那么他说官兵不去,那么,结合刚刚的概率(来的概率:20.46%,不来的概率:79.54%)1. 他说真话 :他说官兵不来,官兵不来的概率是:79.54%*50%=39.77%(实际官兵会来) 他说官兵来, 官兵来的概率是 :20.46%*50%=10.23%2.他说假话:他说官兵来,官兵不来的概率是:20.46*50%=10.23%(实际官兵不会来) 他说官兵不来,官兵来的概率是 :79.54%*50%=39.77%3.最终算出来,官兵来的概率是:20.46%你发现,概率居然没变?你明白了,你假设说真话的概率为50%,那相当于没有任何信息量,等于他什么也没说。妈*的!你作为受过高等教育的土匪头子,还是情不自禁地骂了一句。于是你接着听士兵甲接着说:嘿嘿,皇帝老子要打台湾了。收拾了三藩,接下来收拾台湾了,我们都归施琅统领。士兵乙:真的假的,这你清楚?瞎掰吧?士兵甲:嗨,我骗你做啥?今天我听李二嘎子说的,他说他二叔在施琅手下,他二叔告诉他的。士兵乙:呵呵,李二嘎子的话你也信,那家伙,十句有两句是假话,你信他?.....你听到这里,已经敏锐的觉察到事情的原理了,朝着二当家使了个眼色,你们悄悄撤了。为什么?因为你算了一下,李二嘎子的话可信吗?根据士兵乙的估计这个人,话里80%真话,20%假话,于是你开始计算了:1.李二嘎子说真话:他说官兵要打台湾不来,那么官兵真不来: 80%*79.54%=63.63% 他说官兵不打台湾要来,那么官兵要来 :80%*20.46%=16.37%2.李二嘎子说假话他说官兵要打台湾不来,那么官兵要来 : 20%*20.46%=4.09% 他说官兵不打台湾要来,那么官兵不来 :20%*79.54%=15.91%3.综合下来,官兵要来的概率是4.09%/(4.09%+63.63%)=6.04%看样子,官兵不来的概率很大。但是也不能掉以轻心。所以,你决定,回去之后,不必过份紧张,但要提高警戒,并不断派兄弟下来打探情况。这样看来,应该是可以决策了把。。。
而做决策,就是根据贝叶斯定律,不断用后验概率来修正先验概率的吧。
参考文章:从贝叶斯方法谈到贝叶斯网络Chapter 1 贝叶斯推断的思想全栈必备 贝叶斯方法真的理解贝叶斯公式吗?全概公式和贝叶斯公式的理解
贝叶斯推断及其互联网应用(一):定理简介机器学习(一) —— 浅谈贝叶斯和MCMC(推荐阅读)转载请注明来处,文章首发:贝叶斯公式由浅入深大讲解-AI基础算法入门 - math,数学专栏 - 周陆军的个人网站
长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。而且概率虽然未知,但最起码是一个确定的值。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,而且不论你取了多少次,取得白球的概率θ始终都是1/2,即不随观察结果X 的变化而变化。 这种频率派的观点长期统治着人们的观念,但是:

假设我们有如下的7个球在A,B两个框中,如果我们随便取一个球,已知取到的球来自B框中,那么这个球是白球的概率是多少呢?或者问去除的球是白色,那么取自B框的概率是多少呢?这个问题不是很好解决,直到后来一个名叫Thomas Bayes的人物出现。1.1 贝叶斯方法的提出 托马斯·贝叶斯Thomas Bayes(1702-1763)在世时,并不为当时的人们所熟知,很少发表论文或出版著作,与当时学术界的人沟通交流也很少,用现在的话来说,贝叶斯就是活生生一民间学术“屌丝”,可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”,翻译过来则是:机遇理论中一个问题的解。你可能觉得我要说:这篇论文的发表随机产生轰动效应,从而奠定贝叶斯在学术史上的地位。
事实上,上篇论文发表后,在当时并未产生多少影响,在20世纪后,这篇论文才逐渐被人们所重视。对此,与梵高何其类似,画的画生前一文不值,死后价值连城。 回到上面的例子:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率θ是多少?”贝叶斯认为取得白球的概率是个不确定的值,因为其中含有机遇的成分。比如,一个朋友创业,你明明知道创业的结果就两种,即要么成功要么失败,但你依然会忍不住去估计他创业成功的几率有多大?你如果对他为人比较了解,而且有方法、思路清晰、有毅力、且能团结周围的人,你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式,便是贝叶斯式的思考方式。 继续深入讲解贝叶斯方法之前,先简单总结下频率派与贝叶斯派各自不同的思考方式:
频率派把需要推断的参数θ看做是固定的未知常数,即概率θ虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
而贝叶斯派的观点则截然相反,他们认为参数θ是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数θ的分布。
相对来说,频率派的观点容易理解,所以下文重点阐述贝叶斯派的观点。 贝叶斯派既然把θ看做是一个随机变量,所以要计算θ的分布,便得事先知道θ的无条件分布,即在有样本之前(或观察到X之前),θ有着怎样的分布呢? 比如往台球桌上扔一个球,这个球落会落在何处呢?如果是不偏不倚的把球抛出去,那么此球落在台球桌上的任一位置都有着相同的机会,即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为先验分布,或的无条件分布。 至此,贝叶斯及贝叶斯派提出了一个思考问题的固定模式: 先验分布 π(θ)+ 样本信息χ⇒ 后验分布π(θ|x)上述思考模式意味着,新观察到的样本信息将修正人们以前对事物的认知。换言之,在得到新的样本信息之前,人们对的认知是先验分布 π(θ),在得到新的样本信息后χ,人们对θ的认知为π(θ|x)。而后验分布π(θ|x)一般也认为是在给定样本χ的情况下θ的条件分布,而使达到最大的值称为最大后θMD验估计,类似于经典统计学中的极大似然估计。 综合起来看,则好比是人类刚开始时对大自然只有少得可怜的先验知识,但随着不断是观察、实验获得更多的样本、结果,使得人们对自然界的规律摸得越来越透彻。所以,贝叶斯方法既符合人们日常生活的思考方式,也符合人们认识自然的规律,经过不断的发展,最终占据统计学领域的半壁江山,与经典统计学分庭抗礼。 此外,贝叶斯除了提出上述思考模式之外,还特别提出了举世闻名的贝叶斯定理。1.2 贝叶斯定理 在引出贝叶斯定理之前,先学习几个定义:边缘概率(又称先验概率):某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
联合概率表示两个事件共同发生的概率。A与B的联合概率表示为P(A∩B)或者P(A,B)。
条件概率(又称[b]后验概率)[/b]:事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”,。
接着,考虑一个问题:P(A|B)是在B发生的情况下A发生的可能性。首先,事件B发生之前,我们对事件A的发生有一个基本的概率判断,称为A的先验概率,用P(A)表示;
其次,事件B发生之后,我们对事件A的发生概率重新评估,称为A的后验概率,用P(A|B)表示;
类似的,事件A发生之前,我们对事件B的发生有一个基本的概率判断,称为B的先验概率,用P(B)表示;
同样,事件A发生之后,我们对事件B的发生概率重新评估,称为B的后验概率,用P(B|A)表示。
贝叶斯定理便是基于下述贝叶斯公式:
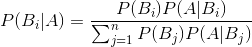
P(A|B)=P(B|A)P(A)/P(B)上述公式的推导其实非常简单,就是从条件概率推出。 根据条件概率的定义,在事件B发生的条件下事件A发生的概率是P(A|B)=P(A∩B)/P(B)同样地,在事件A发生的条件下事件B发生的概率P(B|A)=P(A∩B)/P(A)整理与合并上述两个方程式,便可以得到:P(A|B)P(B)=P(A∩B)=P(B|A)P(A) 接着,上式两边同除以P(B),若P(B)是非零的,我们便可以得到贝叶斯定理的公式表达式:P(A|B)=P(B|A)*P(A)/P(B)
笔者在看《从贝叶斯方法谈到贝叶斯网络》的时候,看到这里,其实已经晕晕的了。P(A|B) 和 P(B|A) 之类的经常让人混淆,@待字闺中的陈老师给出了理解的一个关键点,区分出规律和现象,就是将A看成“规律”,B看成“现象”,那么贝叶斯公式看成:

陈老师在《这的理解贝叶斯公式吗》和《又一个生活中的贝叶斯应用》给出了几个通俗易懂的例子,这里不再赘述。贝叶斯推断的含义
然后搜下,发现其实还有更好阐释,比如对条件概率公式进行变形,可以得到如下形式:
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。所以,条件概率可以理解成下面的式子:后验概率 = 先验概率 x 调整因子这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
贝叶斯定理应用示例:

已知某种疾病的发病率是0.001,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?假定A事件表示得病,那么P(A)为0.001。这就是"先验概率",即没有做试验之前,我们预计的发病率。再假定B事件表示阳性,那么要计算的就是P(A|B)。这就是"后验概率",即做了试验以后,对发病率的估计。根据条件概率公式,
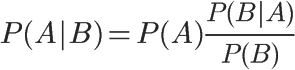
用全概率公式改写分母,
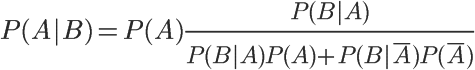
将数字代入,
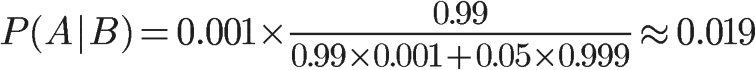
我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的"假阳性",即阳性结果完全不足以说明病人得病。或许换成这个公式 P(A|B)=P(A∩B)/B,看起来更加直白写:阐释:如果没有误报,那么得病率:.001*.99如果是误报,那么得病率为:.05*(1-.0001),所以:p(A|B)=.001*.99/[.99*.001+.05*(1-.0001)]=.019为什么会这样?为什么这种检验的准确率高达99%,但是可信度却不到2%?答案是与它的误报率太高有关。(【习题】如果误报率从5%降为1%,请问病人得病的概率会变成多少?)有兴趣的朋友,还可以算一下"假阴性"问题,即检验结果为阴性,但是病人确实得病的概率有多大。然后问自己,"假阳性"和"假阴性",哪一个才是医学检验的主要风险?
再来一个类似案例:https://www.zhihu.com/question/21134457/answer/169523403一种×××,得了这个×××的人被检测出为阳性的几率为90%,未得这种×××的人被检测出阴性的几率为90%,而人群中得这种×××的几率为1%,一个人被检测出阳性,问这个人得×××的几率为多少? 猛地一看,被检查出阳性,而且得×××的话阳性的概率是90%,那想必这个人应该是难以幸免了。那我们接下来就算算看。我们用 A 表示事件 “测出为阳性”, 用 B1 表示“得×××”, B2表示“未得×××”。根据题目,我们知道如下信息:P(B1)=.01P(B2)=.99P(A|B1)=.9P(A|B2)=.1那么我们现在想得到的是阳性的情况下,得×××的几率 P(B1,A)=P(B1)*P(A|B1)=.01*.09=0.009;
这里P(B1,A)表示的是联合概率,得×××且检测出阳性的概率是人群中得×××的概率乘上得×××时测出是阳性的几率,是0.009。同理可得得×××且检测出阳性的概率:
P(B2,A)=P(B2)*P(A|B2)=.99*.1=.099;这个概率是什么意思呢?其实是指如果人群中有1000个人,检测出阳性并且得×××的人有9个,检测出阳性但未得×××的人有99个。可以看出,检测出阳性并不可怕,不得×××的是绝大多数的,这跟我们一开始的直觉判断是不同的!可直到现在,我们并没有得到所谓的“在检测出阳性的前提下得×××的 概率 ”,怎么得到呢?很简单,就是看被测出为阳性的这108(9+99)人里,9人和99人分别占的比例就是我们要的,也就是说我们只需要添加一个归一化因子(normalization)就可以了。所以阳性得×××的概率 P(B1|A)= .009/(.099+.009)≈.083, 阳性未得×××的概率 P(B2|A)= .099/(.099+.009)≈.917 。 这里 P(B1|A),P(B2|A)中间多了这一竖线
成为了条件概率,而这个概率就是贝叶斯统计中的 后验概率!而人群中患×××与否的概率 P(B1),P(B2) 就是 先验概率!我们知道了先验概率,根据观测值(observation),也可称为test evidence:是否为阳性,来判断得×××的后验概率,这就是基本的贝叶斯思想,我们现在就能得出本题的后验概率的公式为:
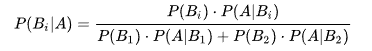
由此就能得到如下的贝叶斯公式的一般形式。我们把上面例题中的 A 变成样本(sample) x , 把 B 变成参数(parameter) \theta , 我们便得到我们的贝叶斯公式:
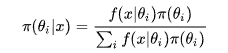
可以看出上面这个例子中,B 事件的分布是离散的,所以在分母用的是求和符号 Σ 。那如果我们的参数θ的分布是连续的呢?没错,那就要用积分,于是我们终于得到了真正的 贝叶斯公式 :
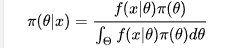
其中π指的是参数的概率分布,π(θ)指的是先验概率,π(θ|x)指的是后验概率, 指的是我们观测到的样本的分布,也就是似然函数(likelihood),记住竖线 | 左边的才是我们需要的。其中积分求的区间Θ指的是参数 θ 所有可能取到的值的域,所以可以看出后验概率π(θ|x) 是在知道 X的前提下在 Θ域内的一个关于 θ 的概率密度分布,每一个θ都有一个对应的可能性(也就是概率)。
作者:徐炎琨链接:https://www.zhihu.com/question/21134457/answer/169523403来源:知乎著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。一个更好理解的例子:链接:https://www.zhihu.com/question/51448623/answer/175907274假设你是一个领导者,或者说,山寨的头目好了。你是远近闻名的土匪头子。哈哈听闻最近官兵换统领了,可能要来剿匪了。这里驻扎的军兵每5年都会换一届统领,新官上任三把火,都想拿你们来开刀。不过每次,你都带领兄弟们打退了官兵的围剿。这次不同了,听说换的是个厉害的角色。因此,你让二头领派人下山去打探消息,看看是不是要来攻山。打探的人回来了,支支吾吾地说:官兵不会来,因为新来统领他妈生病了,回家探病去了。你这个时候,信不信他的话?你看这个回报的人,变毛变色的,说话吞吞吐吐。但是,他也有可能是因为没见过你大头领,回话的时候,有些紧张害怕。你作为一个受过高等教育的人(学过概率论,贝叶斯定理的人),心理开始盘算:1. 官兵每5年来一次,那么今年来的概率就是1/5=20%2. 派出去打探的这小子,说官兵不会来,那么今年来的概率是:03. 嗯?派出去这小子,是不是可靠,不会说的是假话吧?于是,你向旁人了解了一下:1. 三头领劝你好好考虑下,说这个小子虽然人机灵,但是经常是十句话里面有七八句是假的,嘴里没实话。于是你心理又开始盘算:1. 十之七八都假话?能吗?2.姑且认为三当家的话是真的。3.那么派出去这小子,说假话的概率就是 70%~80%:就按75%算把,说真话的概率就是25%4.那么如果他说的真话:他说官兵不来,官兵就不来的概率是:25%*80%=20% 他说官兵来 , 官兵就来的概率是 :25%*20%=5%5. 如果他说的假话:他说官兵不来,官兵 来的概率是:75%*20%=15% 他说官兵来 ,官兵不来的概率是:75%*80%=60%6. 那么他这次口口声声说了:官兵不来那么根据5.的结果:官兵来的概率是 15%官兵不来的概率是 20%比率是: 来/不来=15/20=3/4也就是说,来的概率是3/7 =42.86% 不来的概率是4/7=57.14%【注意】:贝叶斯定律是直接将 15%+20%做分母,两个概率做分子,分别重新计算其条件概率。对你一个决策者来说,这样的比率,太高,显然没有什么意义:于是你决定再派一个自己的亲信兄弟下去打探:三天后回来,回报结果还和刚才结果一样:官兵不会来,统领回家了。这次是你的亲信。应该将概率一下子修正为:官兵来:0 官兵不来 100%但是,这个亲信,虽然忠诚,明显不够机灵。他在打探时,可能被欺骗。他虽然不会骗你,但难保他被别人骗。因此,他的话只能做参考,也不可完全相信:0.参照之前那个兄弟的结果:3/7来,4/7不来1.考虑你的亲信被欺骗的概率为 30%2.那么同样:他被骗:他说官兵不来,官兵不来的概率是:3/7*30%=12.86%(实际官兵会来) 他说官兵来, 官兵来的概率是 :4/7*30%=17.14%他没被骗:他说官兵不来,官兵不来的概率是:4/7*70%=40%(实际官兵不会来)他说官兵来, 官兵来的概率是 :3/7*70%=30%3. 于是他向你报告官兵不来,那么:来/不来=12.86/40于是官兵来的概率就是12.86/(12.86+40)=20.46%看到20.46%?这个概率还是太大,你还是不放心,决定带上二当家,自己亲自下山一趟。于是你门分头走街串巷,茶馆酒肆里转悠,四处打探。最后,还是得出相同的结果。于是你将结果修正为:官兵来的概率:0,不来的概率:100%最后你和二当家在一家酒馆碰头:你说,官兵不来二当家说:我看不一定,我摸到了官兵驻扎的地方,看到了官兵在演习调动。听了这个消息,你大惊失色。你感觉自己可能也被骗了,但是凭自己的经验,被骗的可能性很小只有5%的可能性。于是,你和二当家,约定今晚,趁着月色又摸来了一趟军营。发现确实在调动军队。你心里想:我的乖乖,幸亏过来看了看,否则都没准备,就被官兵包饺子了。你一下子,又将概率修正为:官兵来:100%,官兵不来:0仔细观察了一下动静,听了听。军营里有人小声说话,你和二当家趴在外面听:士兵甲:哎?老四,你知道这回咱们要调哪里去?士兵乙:那我哪里知道,那是上头的事情。士兵甲:嘿!我劝你,把你那点银子趁早寄回家去吧。再晚,怕是没机会了。士兵乙:老三,你瞎说啥,你知道啥,又要打清风寨?士兵甲:嘿,打啥清风寨啊。要打打仗了。你心里想,不打你们山寨?打什么打仗?最近有啥大事?于是你又将那个心理的概率修正为:官兵来:0%,官兵不来:100%这个时候,你突然意识到,自己的思维好像不太对。这后面几次,信息全是压倒性的修正,一次一次,不是0%就是100%,完全不像一个受过高等教育的山寨头领。于是,你默默地多计算了两步。假设这个士兵说真话的概率为50%,那么他说官兵不去,那么,结合刚刚的概率(来的概率:20.46%,不来的概率:79.54%)1. 他说真话 :他说官兵不来,官兵不来的概率是:79.54%*50%=39.77%(实际官兵会来) 他说官兵来, 官兵来的概率是 :20.46%*50%=10.23%2.他说假话:他说官兵来,官兵不来的概率是:20.46*50%=10.23%(实际官兵不会来) 他说官兵不来,官兵来的概率是 :79.54%*50%=39.77%3.最终算出来,官兵来的概率是:20.46%你发现,概率居然没变?你明白了,你假设说真话的概率为50%,那相当于没有任何信息量,等于他什么也没说。妈*的!你作为受过高等教育的土匪头子,还是情不自禁地骂了一句。于是你接着听士兵甲接着说:嘿嘿,皇帝老子要打台湾了。收拾了三藩,接下来收拾台湾了,我们都归施琅统领。士兵乙:真的假的,这你清楚?瞎掰吧?士兵甲:嗨,我骗你做啥?今天我听李二嘎子说的,他说他二叔在施琅手下,他二叔告诉他的。士兵乙:呵呵,李二嘎子的话你也信,那家伙,十句有两句是假话,你信他?.....你听到这里,已经敏锐的觉察到事情的原理了,朝着二当家使了个眼色,你们悄悄撤了。为什么?因为你算了一下,李二嘎子的话可信吗?根据士兵乙的估计这个人,话里80%真话,20%假话,于是你开始计算了:1.李二嘎子说真话:他说官兵要打台湾不来,那么官兵真不来: 80%*79.54%=63.63% 他说官兵不打台湾要来,那么官兵要来 :80%*20.46%=16.37%2.李二嘎子说假话他说官兵要打台湾不来,那么官兵要来 : 20%*20.46%=4.09% 他说官兵不打台湾要来,那么官兵不来 :20%*79.54%=15.91%3.综合下来,官兵要来的概率是4.09%/(4.09%+63.63%)=6.04%看样子,官兵不来的概率很大。但是也不能掉以轻心。所以,你决定,回去之后,不必过份紧张,但要提高警戒,并不断派兄弟下来打探情况。这样看来,应该是可以决策了把。。。
而做决策,就是根据贝叶斯定律,不断用后验概率来修正先验概率的吧。
参考文章:从贝叶斯方法谈到贝叶斯网络Chapter 1 贝叶斯推断的思想全栈必备 贝叶斯方法真的理解贝叶斯公式吗?全概公式和贝叶斯公式的理解
贝叶斯推断及其互联网应用(一):定理简介机器学习(一) —— 浅谈贝叶斯和MCMC(推荐阅读)转载请注明来处,文章首发:贝叶斯公式由浅入深大讲解-AI基础算法入门 - math,数学专栏 - 周陆军的个人网站
相关文章推荐
- 程序员必须知道的10大基础实用算法及其讲解
- 程序员必须知道的10大基础实用算法及其讲解
- 程序员必须知道的10大基础实用算法及其讲解
- 程序员必须知道的10大基础实用算法及其讲解
- 程序员必须知道的10大基础实用算法及其讲解
- 一看就明白的爬虫入门讲解:基础理论篇
- 游戏程序开发必知的10大基础实用算法及其讲解
- 图像基础、OpenCV入门4——图像边缘算法
- 程序员必须知道的十大基础算法及其讲解
- 程序员必须知道的十大基础实用算法及其讲解
- linux 的入门篇基础讲解
- 程序员必须知道的十大基础实用算法及其讲解
- 程序员必须知道的十大基础实用算法及其讲解
- 【广告算法工程师入门 38】模型特征-算法基础之最优化方法
- Dubbo学习总结(1)——Dubbo入门基础与实例讲解
- 算法竞赛入门经典:第六章 数据结构基础 6.12迷宫路径
- Spring框架之基础入门讲解
- android基础入门布局讲解(2)
- 10大基础实用算法及其讲解
- python爬虫由浅入深12---scrapy框架的基础入门
