求字符串最长不连续回文序列的深入研究
2018-04-04 11:34
330 查看
给定一个字符串s,你可以从中删除一些字符,使得剩下的串是一个回文串。如何删除才能使得回文串最长呢? 输出需要删除的字符个数。
这个普遍是使用动态规划,但是都是遍历全部N*N次不断累加后取最后一个数字。
我觉得没有必要全部遍历,于是研究了一下。
1.我们来看一下,这个字符串按照动态规划生成的数组:
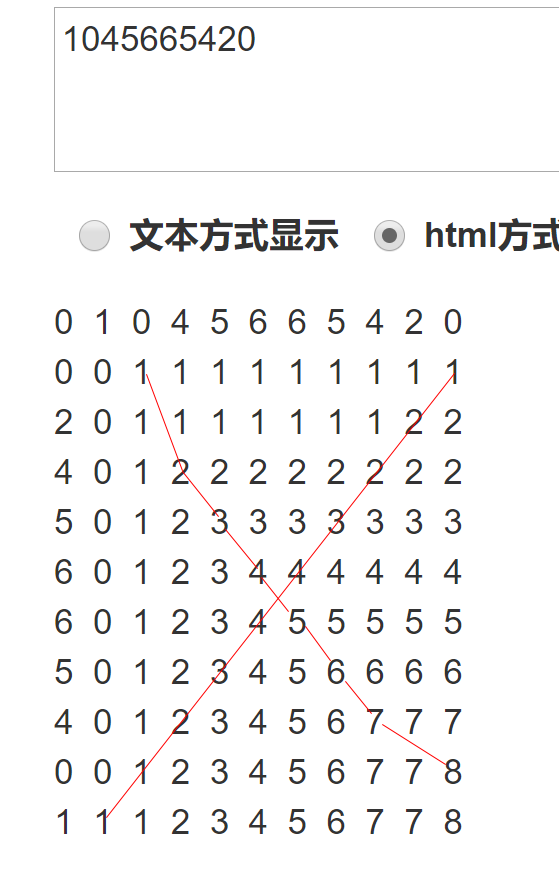
回文的坐标点连线按照次对角线轴对称
我们发现,按照动态规划生成数组,找到的最长回文序列:“04566540”对应i,j的连线,其实是按照次对角线轴对称的,那么是否可以不遍历全部,只遍历对角线左上方呢?答案是肯定的!
那么只需要找出前一半的长度,乘以二不就是我们要的结果了?可是有一个问题啊,让我们看一下下面的情况:
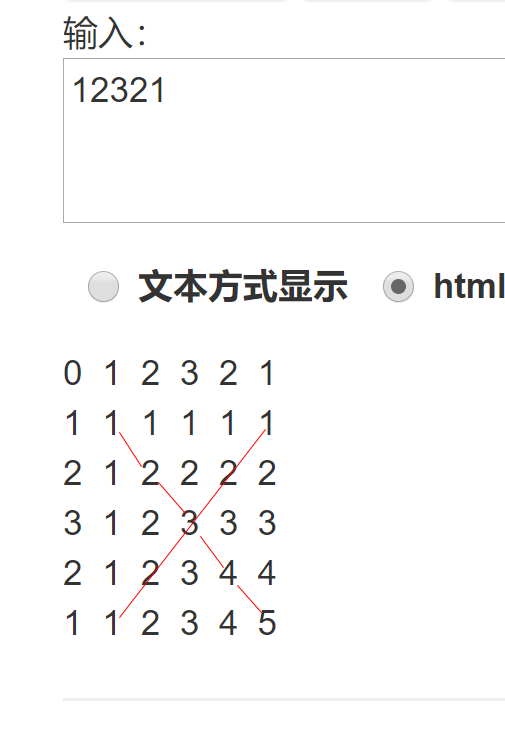
这种情况如何处理?如果判断经过对角线就+1?不不不,这个判断太麻烦,我使用了0.5/0两个数处理,一会代码中可以体现出来。
刚刚说到只遍历一半,那也还是n方啊,没有什么实质性的改变。接下来我想到一个新的点子:我发现其实从一个点所在的“层”到对角线的增量的最大值,是一个固定的值!那么,这个发现有什么用呢??还是通过一个图来看一下:
啊对了,首先要介绍一下这里“层”的概念,其实很简单,就是平行于次对角线的线,从左上角往右下方看:第一层就是一个0,第二层是0 0,那么最后一层就是对角线啦,很显然每一层上的 i + j 都是相等的。

那么我们继续,刚才说到每层到对角线的径直增量(就是每增加一层,数组的值都加一)最大值我推出的公式:
我们看一下这个公式:假设我们用上图的第4层(第二行横着数第一个1,层数从0开始,最后一层对角线就是n-1)举例,径直增量最大值是(n-1 - 4 + 1)/ 2 = 3,同时我们也看到第四层+1(就是这个1的左上角的4,其实在动态规划算法中是边界0来的)往右下看第六层+1第8层+1正好是总增量=增量最大值,这说明了什么呢?这说明了:从第四层的下一层所有节点,即使到对角线的增量达到最大值,也不可能超过第四层的总增量了,那么我们可以直接判断:这个就是我们想要的最大值!也就是3 * 2 = 6!
这个是一个比较特殊的例子,那么通常,一般不会像这样层层递增,这个时候又怎样呢?我们看一下增量最大值和总增量的差值dist=max-total,刚才的例子是dist=0,那么dist=1呢?当dist=1时,很容易想,当前层的下一层,即使达到最大值,也才能与当前总增量相等!再后面的层就更别说了。那么dist>1呢?比如dist=3,同样很容易想到,能够与当前的总增量抗衡的,只有当前层+3之前的这么几层吧?因为+3层,即使达到增量最大值,也才能与当前的总增量相等,后面的层就更不用说了。
总结一下,上面的意思就是说:当dist<=1时,我们可以直接把当前的总增量返回而不用再遍历之后的节点!当dist>1时,我们只需遍历当前层+dist层以里的所有节点而不用再遍历之后的节点!
这样之后,需要遍历的节点就少了很多很多了。
那么,还能不能优化了呢??
当然可以!
先看下图:

先不考虑上面所说的层的优化,正常我的算法遍历应该是这样的,按照蓝色线条方向遍历,那么,我们看到,图中两个三角形区域,在三角形顶点处是会发生递归的(层与层之间的转换也是递归),加入说我们的蓝色线条走到了第一个三角形顶点,发生递归,那么一定涉及到右上方三角形内全部或一部分的节点的遍历,递归返回后,蓝色线条继续前行,那么我们很容易的看到,蓝线又遍历了好几次右上方三角形内部的节点!这不科学,这种遍历完全是无用功!
由此,诞生了一个iRight和一个jBottom(对应于左边界iLeft和jTop)这两个东西是啥?有了这两个东西,就可以对蓝色线条进行限制!就可以避免蓝色线条第二次进入三角形管内的时候进行多余的遍历!
好了,说了这么多,我们直接上代码!虽然这个算法我觉得很不错,但是毕竟递归,我写的仓促,现在没太多时间去消除递归,留着有时间把递归消除,这个算法应该是很不错的,最好的情况是 n/2,调用递归 n/2 次,最坏n方/2,调用递归n+m(m为回文内字符对应上的次数)次,所以以后我必须要消除递归:
import java.util.Scanner;
public class Test {
}
这个普遍是使用动态规划,但是都是遍历全部N*N次不断累加后取最后一个数字。
我觉得没有必要全部遍历,于是研究了一下。
1.我们来看一下,这个字符串按照动态规划生成的数组:

回文的坐标点连线按照次对角线轴对称
我们发现,按照动态规划生成数组,找到的最长回文序列:“04566540”对应i,j的连线,其实是按照次对角线轴对称的,那么是否可以不遍历全部,只遍历对角线左上方呢?答案是肯定的!
那么只需要找出前一半的长度,乘以二不就是我们要的结果了?可是有一个问题啊,让我们看一下下面的情况:

这种情况如何处理?如果判断经过对角线就+1?不不不,这个判断太麻烦,我使用了0.5/0两个数处理,一会代码中可以体现出来。
刚刚说到只遍历一半,那也还是n方啊,没有什么实质性的改变。接下来我想到一个新的点子:我发现其实从一个点所在的“层”到对角线的增量的最大值,是一个固定的值!那么,这个发现有什么用呢??还是通过一个图来看一下:
啊对了,首先要介绍一下这里“层”的概念,其实很简单,就是平行于次对角线的线,从左上角往右下方看:第一层就是一个0,第二层是0 0,那么最后一层就是对角线啦,很显然每一层上的 i + j 都是相等的。

那么我们继续,刚才说到每层到对角线的径直增量(就是每增加一层,数组的值都加一)最大值我推出的公式:
float halfMaxLength(int layerIndex){
return (finalLayer - layerIndex + 1) / 2f;
}我们看一下这个公式:假设我们用上图的第4层(第二行横着数第一个1,层数从0开始,最后一层对角线就是n-1)举例,径直增量最大值是(n-1 - 4 + 1)/ 2 = 3,同时我们也看到第四层+1(就是这个1的左上角的4,其实在动态规划算法中是边界0来的)往右下看第六层+1第8层+1正好是总增量=增量最大值,这说明了什么呢?这说明了:从第四层的下一层所有节点,即使到对角线的增量达到最大值,也不可能超过第四层的总增量了,那么我们可以直接判断:这个就是我们想要的最大值!也就是3 * 2 = 6!
这个是一个比较特殊的例子,那么通常,一般不会像这样层层递增,这个时候又怎样呢?我们看一下增量最大值和总增量的差值dist=max-total,刚才的例子是dist=0,那么dist=1呢?当dist=1时,很容易想,当前层的下一层,即使达到最大值,也才能与当前总增量相等!再后面的层就更别说了。那么dist>1呢?比如dist=3,同样很容易想到,能够与当前的总增量抗衡的,只有当前层+3之前的这么几层吧?因为+3层,即使达到增量最大值,也才能与当前的总增量相等,后面的层就更不用说了。
总结一下,上面的意思就是说:当dist<=1时,我们可以直接把当前的总增量返回而不用再遍历之后的节点!当dist>1时,我们只需遍历当前层+dist层以里的所有节点而不用再遍历之后的节点!
这样之后,需要遍历的节点就少了很多很多了。
那么,还能不能优化了呢??
当然可以!
先看下图:

先不考虑上面所说的层的优化,正常我的算法遍历应该是这样的,按照蓝色线条方向遍历,那么,我们看到,图中两个三角形区域,在三角形顶点处是会发生递归的(层与层之间的转换也是递归),加入说我们的蓝色线条走到了第一个三角形顶点,发生递归,那么一定涉及到右上方三角形内全部或一部分的节点的遍历,递归返回后,蓝色线条继续前行,那么我们很容易的看到,蓝线又遍历了好几次右上方三角形内部的节点!这不科学,这种遍历完全是无用功!
由此,诞生了一个iRight和一个jBottom(对应于左边界iLeft和jTop)这两个东西是啥?有了这两个东西,就可以对蓝色线条进行限制!就可以避免蓝色线条第二次进入三角形管内的时候进行多余的遍历!
好了,说了这么多,我们直接上代码!虽然这个算法我觉得很不错,但是毕竟递归,我写的仓促,现在没太多时间去消除递归,留着有时间把递归消除,这个算法应该是很不错的,最好的情况是 n/2,调用递归 n/2 次,最坏n方/2,调用递归n+m(m为回文内字符对应上的次数)次,所以以后我必须要消除递归:
import java.util.Scanner;
public class Test {
static int total = 0 ;
public static void main(String[] args){
Scanner s = new Scanner(System.in);
while( s.hasNext()){
String str = s.next();
logln( str.length() - find(str) );
}
}
static int yBottom , xRight , finalLayer;
static int find(String str){
if(str.length() <= 1)return 1;
xRight = yBottom = finalLayer = str.length() - 1;
float res = 2 * findLength(str.toCharArray() ,
0 , 0 , -1 , -1 , 0 , str.length() - 1 , 0.5f );
return (int)res;
}
/**
*
* @param str 字符串数组
* @param i 当前x坐标
* @param j 当前y坐标
* @param iLeft x坐标左边界
* @param jTop y坐标上边界
* @param curValue
* @param endLayer 计算所需最后的层
* @param seed 用于补充0.5,因为是只计算一半
* @return
*/
static float findLength(char[] str,
int i,
int j,
int iLeft ,
int jTop ,
float curValue,
int endLayer,
float seed){
int curLayer = i + j;
if( curLayer > endLayer ) return curValue;
if( curLayer == endLayer ) return curValue + (str[i] == str[str.length - 1 - j] ? seed : 0);
int ii = i , jj = j ;
float curLen = 0;
while(ii > iLeft ){
if(str[ii] == str[str.length - 1 - jj] && ( jj <= yBottom || ii <= xRight )){
curLen = findLength(str , ii+1 , jj+1 , ii , jj , curValue + 1 , finalLayer , 0.5f);
float delta = curLen - curValue;
xRight = Math.min( xRight , ii );
yBottom = Math.min( yBottom , jj );
int dist = (int)(halfMaxLength( curLayer ) - delta ) ;
if(dist <= 1)break;
endLayer = curLayer + dist;
}
ii--;jj++;
}
if(ii == iLeft)
return Math.max( curLen , findLength( str, i+1 , j , iLeft , jTop , curValue , endLayer , endLayer == finalLayer ? 0.5f : 0) );
else return curLen;
}
static float halfMaxLength(int layerIndex){ return (finalLayer - layerIndex + 1) / 2f; }
static void log(Object...objs){
for(Object obj : objs) System.out.print(obj);
}
4000
static void logln(Object...objs){
for(Object obj : objs) System.out.println(obj);
}
}
能力有限,请各路大佬指点
消除递归心得在另一篇文章里模拟状态机消除递归心得相关文章推荐
- 求字符串最长不连续回文序列的深入研究
- 最长公共子串、最长公共子序列、最长回文子串、模式匹配、最大子序列--字符串问题整理
- 求两个字符串的最长的连续公共子串和求两个字符串的公共子序列
- 数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- ] 找工作知识储备(2)---数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- 找工作知识储备---数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- 一个看似简单却复杂的问题:求两个字符串的 左向右匹配 所有的 最长连续的 公共子字符串( 在每个字符串中先后次序相同的) 序列
- 如何求最长连续公共子序列和最长连续子字符串
- 利用Manacher算法寻找字符串中的最长回文序列(palindrome)
- 求最长连续公共子序列和最长连续子字符串
- 数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- 数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- 最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- 求给定字符串中最长回文序列
- 数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串
- 求一个字符串中的最长回文序列
- 利用最长公子序列求回文字符串
- 【算法】寻找字符串中最长的回文序列
- 找出一个字符串中最长的连续回文
- 数组字符串那些经典算法:最大子序列和,最长递增子序列,最长公共子串,最长公共子序列,字符串编辑距离,最长不重复子串,最长回文子串 (转)
