最大熵模型 Maximum Entropy Model

熵的概念在统计学习与机器学习中真是很重要，熵的介绍在这里：信息熵 Information Theory 。今天的主题是最大熵模型（Maximum Entropy Model，以下简称MaxEnt），MaxEnt 是概率模型学习中一个准则，其思想为：在学习概率模型时，所有可能的模型中熵最大的模型是最好的模型；若概率模型需要满足一些约束，则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。最大熵原理指出，对一个随机事件的概率分布进行预测时，预测应当满足全部已知的约束，而对未知的情况不要做任何主观假设。在这种情况下，概率分布最均匀，预测的风险最小，因此得到的概率分布的熵是最大。直观理解 MaxEnt在求解概率模型时，当没有任何约束条件则只需找到熵最大的模型，比如预测一个骰子的点数，每个面为 1616， 是， 当模型有一些约束条件之后，首先要满足这些约束条件， 然后在满足约束的集合中寻找熵最大的模型，该模型对未知的情况不做任何假设，未知情况的分布是最均匀的。举例来说对于随机变量 XX ，其可能的取值为 {A,B,C}{A,B,C} ，没有任何约束的情况下下，各个值等概率得到的 MaxEnt 模型为：P(A)=P(B)=P(C)=13P(A)=P(B)=P(C)=13当给定一个约束 P(A)=12P(A)=12 , 满足该约束条件下的 MaxEnt 模型是：
P(A)=12P(A)=12
P(B)=P(C)=14P(B)=P(C)=14如果用欧式空间中的 simplex 来表示随机变量 XX 的话，则 simplex 中三个顶点分别代表随机变量 XX 的三个取值 A, B, C , 这里定义 simplex  中任意一点 pp 到三条边的距离之和（恒等于三角形的高）为 1，点到其所对的边为该取值的概率，比如任给一点pp ，则P(A)P(A) 等于 pp 到  边 BC 的距离，如果给定如下概率：
P(A)=1,P(B)=P(C)=0P(A)=1,P(B)=P(C)=0
P(A)=P(B)=P(C)=13P(A)=P(B)=P(C)=13分别用下图表示以上两种情况：

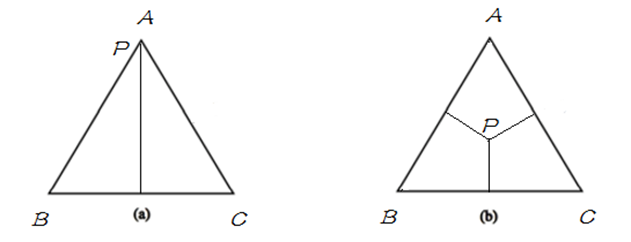
明白了 simplex 的定义之后，将其与概率模型联系起来，在 simplex 中，不加任何约束，整个概率空间的取值可以是 simplex 中的任意一点，只需找到满足最大熵条件的的即可；当引入一个约束条件 C1C1 后，如下图中 (b),模型被限制在 C1C1 表示的直线上，则应在满足约束 C1C1 的条件下来找到熵最大的模型；当继续引入条件 C2C2 后，如图(c)，模型被限制在一点上，即此时有唯一的解；当 C1C1 与 C2C2 不一致时，如图(d)，此时模型无法满足约束，即无解。在 MaxEnt 模型中，由于约束从训练数据中取得，所以不会出现不一致。即不会出现(d) 的情况。

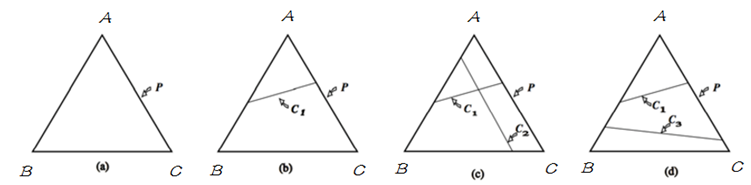
接下来以统计建模的形式来描述 MaxEnt 模型，给定训练数据 {(xi,yi)}Ni=1{(xi,yi)}i=1N ，现在要通过Maximum Entrop 来建立一个概率判别模型，该模型的任务是对于给定的 X=xX=x 以条件概率分布 P(Y|X=x)P(Y|X=x) 预测 YY 的取值。根据训练语料能得出 (X,Y)(X,Y)的经验分布， 得出部分 (X,Y)(X,Y) 的概率值，或某些概率需要满足的条件,即问题变成求部分信息下的最大熵或满足一定约束的最优解，约束条件是靠特征函数来引入的，首先先回忆一下函数期望的概念
对于随机变量 X=xi,i=1,2,…X=xi,i=1,2,…，则可以得到：随机变量期望: 对于随机变量 XX ，其数学期望的形式为 E(X)=∑ixipiE(X)=∑ixipi随机变量函数期望：若 Y=f(X)Y=f(X) ， 则关于 XX 的函数 YY 的期望： E(Y)=∑if(xi)piE(Y)=∑if(xi)pi.特征函数特征函数 f(x,y)f(x,y) 描述 xx 与 yy 之间的某一事实，其定义如下：f(x,y)={1,0, 当 x、y 满足某一事实. 不满足该事实.f(x,y)={1, 当 x、y 满足某一事实.0, 不满足该事实.特征函数 f(x,y)f(x,y) 是一个二值函数， 当 xx 与 yy 满足事实时取值为 1 ，否则取值为 0 。比如对于如下数据集：

数据集中，第一列为 Y ，右边为 X ，可以为该数据集写出一些特征函数，数据集中得特征函数形式如下：
f(x,y)={1,0, if x=Cloudy and y=Outdoor. else.f(x,y)={1, if x=Cloudy and y=Outdoor.0, else.为每个 <feature,label> 对 都做一个如上的特征函数，用来描述数据集数学化。约束条件接下来看经验分布，现在把训练数据当做由随机变量 (X,Y)(X,Y) 产生,则可以根据训练数据确定联合分布的经验分布 P˜(X,Y)P~(X,Y) 与边缘分布的经验分布 P˜(X)P~(X) :
P˜(X=x,Y=y)P˜(X=x)=count(X=x,Y=y)N=count(X=x)NP~(X=x,Y=y)=count(X=x,Y=y)NP~(X=x)=count(X=x)N
用 EP˜(f)EP~(f) 表示特征函数 f(x,y)f(x,y) 关于经验分布 P˜(X,Y)P~(X,Y) 的期望，可得：
EP˜(f)=∑x,yP˜(x,y)f(x,y)=1N∑x,yf(x,y)EP~(f)=∑x,yP~(x,y)f(x,y)=1N∑x,yf(x,y)P˜(x,y)P~(x,y) 前面已经得到了，数数 f(x,y)f(x,y) 的次数就可以了，由于特征函数是对建立概率模型有益的特征，所以应该让 MaxEnt 模型来满足这一约束，所以模型 P(Y|X)P(Y|X)  关于函数 ff 的期望应该等于经验分布关于 ff 的期望，模型 P(Y|X)P(Y|X) 关于 ff 的期望为：
EP(f)=∑x,yP(x,y)f(x,y)≈∑x,yP˜(x)P(y|x)f(x,y)EP(f)=∑x,yP(x,y)f(x,y)≈∑x,yP~(x)P(y|x)f(x,y)经验分布与特征函数结合便能代表概率模型需要满足的约束，只需使得两个期望项相等， 即 EP(f)=EP˜(f)EP(f)=EP~(f) ：
∑x,yP˜(x)p(y|x)f(x,y)=∑x,yP˜(x,y)f(x,y)∑x,yP~(x)p(y|x)f(x,y)=∑x,yP~(x,y)f(x,y)上式便为 MaxEnt 中需要满足的约束，给定 nn 个特征函数 fi(x,y)fi(x,y) ，则有 nn 个约束条件，用 CC 表示满足约束的模型集合：
C={P | EP(fi)=EP˜(fi),I=1,2,…,n}C={P | EP(fi)=EP~(fi),I=1,2,…,n}从满足约束的模型集合 CC 中找到使得 P(Y|X)P(Y|X) 的熵最大的即为 MaxEnt 模型了。最大熵模型关于条件分布 P(Y|X)P(Y|X) 的熵为：
H(P)=–∑x,yP(y,x)logP(y|x)=–∑x,yP˜(x)P(y|x)logP(y|x)H(P)=–∑x,yP(y,x)logP(y|x)=–∑x,yP~(x)P(y|x)logP(y|x)首先满足约束条件然后使得该熵最大即可，MaxEnt 模型 P∗P∗ 为：
P∗=argmaxP∈CH(P)  或  P∗=argminP∈C−H(P)P∗=argmaxP∈CH(P)  或  P∗=argminP∈C−H(P)综上给出形式化的最大熵模型：
给定数据集 {(xi,yi)}Ni=1{(xi,yi)}i=1N，特征函数 fi(x,y)，i=1,2…,nfi(x,y)，i=1,2…,n ，根据经验分布得到满足约束集的模型集合 CC ：minP∈C  ∑x,yP˜(x)P(y|x)logP(y|x) s.t.   Ep(fi)=EP˜(fi)         ∑yP(y|x)=1minP∈C  ∑x,yP~(x)P(y|x)logP(y|x) s.t.   Ep(fi)=EP~(fi)         ∑yP(y|x)=1
MaxEnt 模型的求解MaxEnt 模型最后被形式化为带有约束条件的最优化问题，可以通过拉格朗日乘子法将其转为无约束优化的问题，引入拉格朗日乘子：w0,w1,…,wnw0,w1,…,wn， 定义朗格朗日函数 L(P,w)L(P,w):L(P,w)=−H(P)+w0(1−∑yP(y|x))+∑i=1nwi(EP˜(fi)−Ep(fi))=∑x,yP˜(x)P(y|x)logP(y|x)+w0(1−∑yP(y|x))+∑i=1nwi(∑x,yP˜(x,y)f(x,y)−∑x,yP˜(x)p(y|x)f(x,y))L(P,w)=−H(P)+w0(1−∑yP(y|x))+∑i=1nwi(EP~(fi)−Ep(fi))=∑x,yP~(x)P(y|x)logP(y|x)+w0(1−∑yP(y|x))+∑i=1nwi(∑x,yP~(x,y)f(x,y)−∑x,yP~(x)p(y|x)f(x,y))现在问题转化为: minP∈CL(P,w)minP∈CL(P,w) ，拉格朗日函数 L(P,w)L(P,w) 的约束是要满足的 ，如果不满足约束的话，只需另 wi→+∞wi→+∞，则可得 L(P,w)→+∞L(P,w)→+∞ ，因为需要得到极小值，所以约束必须要满足，满足约束后可得： L(P,w)=maxL(P,w)L(P,w)=maxL(P,w) ，现在问题可以形式化为便于拉格朗日对偶处理的极小极大的问题：
minP∈CmaxwL(P,w)minP∈CmaxwL(P,w)由于 L(P,w)L(P,w) 是关于 P 的凸函数，根据拉格朗日对偶可得 L(P,w)L(P,w) 的极小极大问题与极大极小问题是等价的：
minP∈CmaxwL(P,w)=maxwminP∈CL(P,w)minP∈CmaxwL(P,w)=maxwminP∈CL(P,w)现在可以先求内部的极小问题 minP∈CL(P,w)minP∈CL(P,w) ，minP∈CL(P,w)minP∈CL(P,w) 得到的解为关于 ww 的函数，可以记做 Ψ(w)Ψ(w) ：
Ψ(w)=minP∈CL(P,w)=L(Pw,w)Ψ(w)=minP∈CL(P,w)=L(Pw,w)上式的解 PwPw 可以记做：
Pw=argminP∈CL(P,w)=Pw(y|x)Pw=argminP∈CL(P,w)=Pw(y|x)由于求解 PP 的最小值 PwPw ,只需对于 P(y|x)P(y|x) 求导即可,令导数等于 0 即可得到 Pw(y|x)Pw(y|x) ：
∂L(P,w)∂P(y|x)⇒P(y|x)=∑x,yP˜(x)(logP(y|x)+1)−∑yw0−∑x,y(P˜(x)∑i=1nwifi(x,y))=∑x,yP˜(x)(logP(y|x)+1−w0−∑i=1nwifi(x,y))=0=exp(∑i=1nwifi(x,y)+w0−1)=exp(∑ni=1wifi(x,y))exp(1−w0)∂L(P,w)∂P(y|x)=∑x,yP~(x)(logP(y|x)+1)−∑yw0−∑x,y(P~(x)∑i=1nwifi(x,y))=∑x,yP~(x)(logP(y|x)+1−w0−∑i=1nwifi(x,y))=0⇒P(y|x)=exp(∑i=1nwifi(x,y)+w0−1)=exp(∑i=1nwifi(x,y))exp(1−w0)由于 ∑yP(y|x)=1∑yP(y|x)=1，可得:
∑yP(y|x)=1⇒1exp(1−w0)∑yexp(∑i=1nwifi(x,y))=1∑yP(y|x)=1⇒1exp(1−w0)∑yexp(∑i=1nwifi(x,y))=1进而可以得到：
exp(1−w0)=∑yexp(∑i=1nwifi(x,y))exp(1−w0)=∑yexp(∑i=1nwifi(x,y))这里  exp(1−w0)exp(1−w0) 起到了归一化的作用，令 Zw(x)Zw(x) 表示 exp(1−w0)exp(1−w0) ，便得到了 MaxEnt 模型 ：
Pw(y|x)Zw(x)=1Zw(x)exp(∑i=1nwifi(x,y))=∑yexp(∑i=1nwifi(x,y))Pw(y|x)=1Zw(x)exp(∑i=1nwifi(x,y))Zw(x)=∑yexp(∑i=1nwifi(x,y))
这里 fi(x,y)fi(x,y) 代表特征函数，wiwi 代表特征函数的权值， Pw(y|x)Pw(y|x)  即为 MaxEnt 模型，现在内部的极小化求解得到关于 ww 的函数，现在求其对偶问题的外部极大化即可，将最优解记做 w∗w∗:w∗=argmaxwΨ(w)w∗=argmaxwΨ(w)所以现在最大上模型转为求解 Ψ(w)Ψ(w) 的极大化问题，求解最优的 w∗w∗ 后， 便得到了所要求的MaxEnt 模型，将 Pw(y|x)Pw(y|x) 带入 Ψ(w)Ψ(w) ，可得：
Ψ(w)=∑x,yP˜(x)Pw(y|x)logPw(y|x)+∑i=1nwi(∑x,yP˜(x,y)f(x,y)−∑x,yP˜(x)Pw(y|x)f(x,y))=∑x,yP˜(x,y)∑i=1nwifi(x,y)+∑x,yP˜(x)Pw(y|x)(logPw(y|x)−∑i=1nwifi(x,y))=∑x,yP˜(x,y)∑i=1nwifi(x,y)+∑x,yP˜(x)Pw(y|x)logZw(x)=∑x,yP˜(x,y)∑i=1nwifi(x,y)+∑xP˜(x)logZw(x)∑yPw(y|x)=∑x,yP˜(x,y)∑i=1nwifi(x,y)+∑xP˜(x)logZw(x)Ψ(w)=∑x,yP~(x)Pw(y|x)logPw(y|x)+∑i=1nwi(∑x,yP~(x,y)f(x,y)−∑x,yP~(x)Pw(y|x)f(x,y))=∑x,yP~(x,y)∑i=1nwifi(x,y)+∑x,yP~(x)Pw(y|x)(logPw(y|x)−∑i=1nwifi(x,y))=∑x,yP~(x,y)∑i=1nwifi(x,y)+∑x,yP~(x)Pw(y|x)logZw(x)=∑x,yP~(x,y)∑i=1nwifi(x,y)+∑xP~(x)logZw(x)∑yPw(y|x)=∑x,yP~(x,y)∑i=1nwifi(x,y)+∑xP~(x)logZw(x)以上推倒第二行到第三行用到以下结论：
Pw(y|x)=1Zw(x)exp(∑i=1nwifi(x,y))⇒logPw(y|x)=∑i=1nwifi(x,y)−logZw(x)Pw(y|x)=1Zw(x)exp(∑i=1nwifi(x,y))⇒logPw(y|x)=∑i=1nwifi(x,y)−logZw(x)倒数第二行到最后一行是由于：∑yPw(y|x)=1∑yPw(y|x)=1，最终通过一系列极其复杂的运算，得到了需要极大化的式子：
maxp∈C∑x,yP˜(x,y)∑i=1nwifi(x,y)+∑xP˜(x)logZw(x)maxp∈C∑x,yP~(x,y)∑i=1nwifi(x,y)+∑xP~(x)logZw(x)极大化似然估计解法这太难了，有没有简单又 work 的方式呢？ 答案是有的，就是极大似然估计 MLE 了，这里有训练数据得到经验分布 P˜(x,y)P~(x,y) ， 待求解的概率模型 P(Y|X)P(Y|X) 的似然函数为：
LP˜(Pw)=log∏x,yP(y|x)P˜(x,y)=∑x,yP˜(x,y)logP(y|x)LP~(Pw)=log∏x,yP(y|x)P~(x,y)=∑x,yP~(x,y)logP(y|x)将 Pw(y|x)Pw(y|x) 带入以下公式可以得到：
LP˜(Pw)=∑x,yP˜(x,y)logP(y|x)=∑x,yP˜(x,y)(∑i=1nwifi(x,y)−logZw(x))=∑x,yP˜(x,y)∑i=1nwifi(x,y)−∑x,yP˜(x,y)logZw(x)=∑x,yP˜(x,y)∑i=1nwifi(x,y)−∑xP˜(x)logZw(x)LP~(Pw)=∑x,yP~(x,y)logP(y|x)=∑x,yP~(x,y)(∑i=1nwifi(x,y)−logZw(x))=∑x,yP~(x,y)∑i=1nwifi(x,y)−∑x,yP~(x,y)logZw(x)=∑x,yP~(x,y)∑i=1nwifi(x,y)−∑xP~(x)logZw(x)显而易见，拉格朗日对偶得到的结果与极大似然得到的结果时等价的，现在只需极大化似然函数即可，顺带优化目标中可以加入正则项，这是一个凸优化问题，一般的梯度法、牛顿法都可解之，专门的算法有GIS IIS 算法，。这里给出来做下参考吧！ == 参考文献：《统计学习方法》http://blog.csdn.net/itplus/article/details/26550201http://www.cnblogs.com/hexinuaa/p/3353479.htmlA Maximum Entropy Approach A Maximum Entropy ApproachClassical Probabilistic Models and Conditional Random Fields