[聚类一]之距离计算

距离计算

我们通常采用计算“距离”的方法来度量不同样本之间的相似性，进而判断该样本的大致类别。距离首先是一个几何概念，用dist(⋅,⋅)dist(⋅,⋅)表示，其中最为任熟悉的是二维和三维几何空间的欧几里德距离，随着数据维度的增大，距离在维数、幂次数等方面被推广了，距离被抽象为满足一些基本性质：

 非负性：dist(xi,xj)≥0;(1.1)(1.1)dist(xi,xj)≥0;

 同一性：dist(xi,xj)=0，当且仅当xi=xj;(1.2)(1.2)dist(xi,xj)=0，当且仅当xi=xj;

 对称性：dist(xi,xj)=dist(xj,xi);(1.3)(1.3)dist(xi,xj)=dist(xj,xi);

 直递性：dist(xi,xj)≤dist(xi,xk)+dist(xk,xj);(1.3)(1.3)dist(xi,xj)≤dist(xi,xk)+dist(xk,xj);

需要注意的是，用于相似度度量的距离未必一定满足以上所有的性质，尤其是直递性(1.3)。例如在某些任务中我们可能希望有这样的相似度度量：“人”“马”分别与“人马”相似，但“人”与“马”很不相似；要达到这个目的，可以令“人”“马”与“人马”之间的距离很小，但“人”与“马”之间的距离很大，如下图所示：



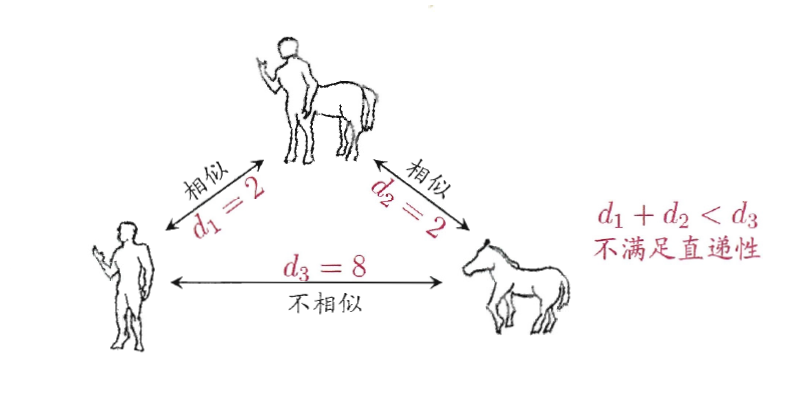
为了让大家对各种距离计算方法的应用场景有个清楚的认识，在讲距离计算方法之前，我先介绍一下几个名词。

属性：即样本本身所具有的特征，样本空间中的维度，就是属性的个数。

连续属性：样本的属性在定义域上有无穷多个可能的取值，比如说树的高度在[7,10][7,10]米之间，其取值是无穷多的。

离散属性：样本的属性在定义域上是有限个取值，比如说树的品种，肯定是有限的，只能从{白杨树,柳树,...,桃树}{白杨树,柳树,...,桃树}中取值，那么树的品种就属于离散属性

有序属性：就是说，属性的值能直接用来计算计算距离。例如树的高度。

无序属性：就是说，属性的值不能直接用来计算计算距离。例如树的品种。

因此所有样本的属性都可划分为有序属性或者无序属性，或者同时具有有序属性和无序属性，这里我们成为混合属性。针对于有序属性的样本，我们常常使用闵科夫斯基距离计算公式来衡量样本之间的相似度，针对于无序属性的样本我们可采用VDMVDM (Value(Value DiffrenceDiffrence Metric)Metric)

graph TD;
连续属性-->有序属性;
离散属性-->有序属性;
离散属性-->无序属性;
有序属性-->闵科夫斯基;
无序属性-->VDM;

闵科夫斯基距离（Minkowski distance）

distmk(xi,xj)=(∑u=1n|xiu−xju|p)1p,p≥1(2.1)(2.1)distmk(xi,xj)=(∑u=1n|xiu−xju|p)1p,p≥1

当 p=2p=2时，闵科夫斯基距离即欧式距离（Euclidean distance）

distmk(xi,xj)=∑u=1n|xiu−xju|2−−−−−−−−−−−−√(2.2)(2.2)distmk(xi,xj)=∑u=1n|xiu−xju|2

python实现：

def eucldist_forloop(coords1, coords2):
""" Calculates the euclidean distance between 2 lists of coordinates. """
dist = 0
for (x, y) in zip(coords1, coords2):
dist += (x - y)**2
return dist**0.5

或者

# 生成器表达式

def eucldist_generator(coords1, coords2):
""" Calculates the euclidean distance between 2 lists of coordinates. """
return sum((x - y)**2 for x, y in zip(coords1, coords2))**0.5

或者

# NumPy版本

def eucldist_vectorized(coords1, coords2):
""" Calculates the euclidean distance between 2 lists of coordinates. """
return np.sqrt(np.sum((coords1 - coords2)**2))

或者

# NumPy 内建函数

np.linalg.norm(np_c1 - np_c2)

或者

# 根据scipy库求解

from scipy.spatial.distance import pdist
X=np.vstack([np_c1,np_c2])
d2=pdist(X)

当p→∞p→∞时，闵科夫斯基距离即切比雪夫距离(Chebyshev Distance)

python实现:

# NumPy 内建函数

np.linalg.norm(np_c1 - np_c2,ord=np.inf)

或者

# 根据scipy库求解

from scipy.spatial.distance import pdist
X=np.vstack([np_c1,np_c2])
d2=pdist(X,'chebyshev')

当p=1p=1时，闵科夫斯基距离即曼哈顿距离(Manhattan distance)

python实现:

# NumPy 内建函数

np.linalg.norm(np_c1 - np_c2,ord=1)

#根据scipy库求解

from scipy.spatial.distance import pdist
X=np.vstack([np_c1,np_c2])
d2=pdist(X,'cityblock')

distmk(xi,xj)=∑u=1n|xiu−xju|(2.3)(2.3)distmk(xi,xj)=∑u=1n|xiu−xju|

VDM(Value Difference Metric)

令mu,amu,a表示属性uu上取值为aa的样本数，mu,a,imu,a,i表示在第ii个样本簇中在属性uu上取值为aa的样本数，kk为样本簇数，则属性uu上两个离散值aa与bb之间的VDM距离为VDMp(a,b)=∑i=1k∣∣∣mu,a,imu,a−mu,b,imu,b∣∣∣(2.4)(2.4)VDMp(a,b)=∑i=1k|mu,a,imu,a−mu,b,imu,b|

针对与混合属性的样本，我们可以将闵科夫斯基距离和VDM结合处理。假定有ncnc个有序属性，n−ncn−nc个无序属性，不失一般性，令有序属性排列在无序属性之前，则

MinkovDMp(xi,xj)=(∑ncu=1|xiu−xju|p+∑nu=nc+1VDMp(xiu−xju)1p)(2.5)(2.5)MinkovDMp(xi,xj)=(∑u=1nc|xiu−xju|p+∑u=nc+1nVDMp(xiu−xju)1p)

注意的是：当样本空间不同属性的重要性不同时，可使用“加权距离”(weighted distance)。以加权的闵科夫斯基距离为例：

distwmk(xi,xj)=(w1⋅|xi1−xj1|p+...+wn⋅|xin−xjn|p)1/p(2.6)(2.6)distwmk(xi,xj)=(w1⋅|xi1−xj1|p+...+wn⋅|xin−xjn|p)1/p

其中权重wi≥0(i=1,2,...,n)wi≥0(i=1,2,...,n)表征不同属性的重要性。通常∑ni=1wi=1∑i=1nwi=1

余弦距离(Cosine Similarity)

利用闵可夫斯基度量对高维数据进行聚类通常是无效的，因为样本之间的距离随着维数的增加而增加。余弦距离测量两个矢量之间的夹角，而不是两个矢量之间的幅值差。它适用于高维数据聚类时相似度测量。cos(x⃗ ,y⃗ )=y⃗ Tx⃗ ∥x⃗ ∥∥y⃗ ∥(2.7)(2.7)cos(x→,y→)=y→Tx→‖x→‖‖y→‖

python实现:

# NumPy 内建函数

np.dot(vector1,vector2)/(np.linalg.norm(vector1)*(np.linalg.norm(vector2)))

马氏距离(Mahalanobis Distance)

马氏距离，即数据的协方差距离，于欧式距离不同的是它考虑到各属性之间的联系，如考虑性别信息时会带来一条关于身高的信息，因为二者有一定的关联度，而且独立于测量尺度。

Dmah(x,y)=(p−q)Σ−1(p−q)T(2.8)(2.8)Dmah(x,y)=(p−q)Σ−1(p−q)T

其中ΣΣ是数据集x,y的协方差矩阵。马氏距离在非奇异变换下是不变的，可用来检测异常值(outliers)

需要注意的是：马氏距离是建立在总体样本的基础上的，这一点可以从上述协方差矩阵的解释中可以得出，也就是说，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；其次要求总体样本的协方差矩阵存在。

python实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

#马氏距离要求样本数要大于维数，否则无法求协方差矩阵
#此处进行转置，表示10个样本，每个样本2维
X=np.vstack([x,y])
XT=X.T

#方法一：根据公式求解
S=np.cov(X)   #两个维度之间协方差矩阵
SI = np.linalg.inv(S) #协方差矩阵的逆矩阵
#马氏距离计算两个样本之间的距离，此处共有10个样本，两两组合，共有45个距离。
n=XT.shape[0]
d1=[]
for i in range(0,n):
for j in range(i+1,n):
delta=XT[i]-XT[j]
d=np.sqrt(np.dot(np.dot(delta,SI),delta.T))
d1.append(d)

#方法二：根据scipy库求解
from scipy.spatial.distance import pdist
d2=pdist(XT,'mahalanobis')

KL散度(KL divergence)

KL散度又称为相对熵，它是描述对随机变量X的两个概率分布PP和QQ差别的非对称性度量，它不满足距离基本性质中的对称性和直递性。特别的，在信息论中，DKL(P(x)||Q(x))DKL(P(x)||Q(x))表示当概率分布Q(x)Q(x)来拟合真实分布P(x)P(x)时，产生的信息损耗。

DKL(P(x)||Q(x))=∑x∈Xln(p(x)q(x))(2.9)(2.9)DKL(P(x)||Q(x))=∑x∈Xln(p(x)q(x))

连续形式如下：

DKL(P(x)||Q(x))=∫∞−∞ln(p(x)q(x))(2.10)(2.10)DKL(P(x)||Q(x))=∫−∞∞ln(p(x)q(x))

python实现：

import numpy as np
import scipy.stats

# 随机生成两个离散型分布
x = [np.random.randint(1, 11) for i in range(10)]
print(x)
print(np.sum(x))
px = x / np.sum(x)
print(px)
y = [np.random.randint(1, 11) for i in range(10)]
print(y)
print(np.sum(y))
py = y / np.sum(y)
print(py)

# 利用scipy API进行计算
# scipy计算函数可以处理非归一化情况，因此这里使用
# scipy.stats.entropy(x, y)或scipy.stats.entropy(px, py)均可
KL = scipy.stats.entropy(x, y)
print(KL)

# 编程实现
KL = 0.0
for i in range(10):
KL += px[i] * np.log(px[i] / py[i])
# print(str(px[i]) + ' ' + str(py[i]) + ' ' + str(px[i] * np.log(px[i] / py[i])))

print(KL)

参考文献

[1]. 周志华，机器学习，清华大学出版社，2016

[2]. 距离度量以及python实现(一)

[3]. python 3计算KL散度（KL Divergence）

<个人网页blog已经上线，一大波干货即将来袭：https://faiculty.com/>

/* 版权声明：公开学习资源，只供线上学习，不可转载，如需转载请联系本人 .*/

QQ交流群：451429116