[贝叶斯九]之EM算法

一、简单介绍

EM(Expectaion Maximization)算法(又称为期望最大化方法)是一种迭代算法，Dempster等人在1977年总结提出来的。简单来说EM算法就是一种含有隐变量的概率模型参数的极大似然估计。EM算法的每次迭代由两步组成：第一是求期望，第二是求极大。EM算法在机器学习中有极为广泛的应用。如常被用来学习高斯混合模型(Gaussian mixture model, 简称GMM)的参数。

那么什么是含有隐变量的概率模型？隐变量的概率模型？这里举一个常用的三硬币例子，假设我们有三枚硬币：A、B和C，他们的质地都是不均匀的，假设他们正面朝上的概率分别是：a、b和c。现在弄一个抛硬币的规则，先抛A硬币，如果A正面朝上，那么就抛B硬币，否则就抛C硬币。最后记下最终结果，正面朝上记为1，否则记为0。现在进行10次该实验，假如得到的结果如下： 1，0，0，1，1，1，0，1，0，0。这个时候我们其实只得到了最终的结果，并不知道是B还是C硬币的结果，因为不知道每次A硬币的结果。这个时候A硬币的抛掷就可以认为是一个隐含变量。但是问题是如何根据这个结果来估计这三个参数呢？

二、理论推导

2.1 算法思想

在解决例子问题之前，我们先进行一些所谓枯燥的数学化定义，这样或许能帮助理解和记忆。首先，假设YY是最终观测到的变量集(上述硬币中的最终正反面结果)，ZZ是隐变量集(A硬币结果)，Θ(a,b,c)Θ(a,b,c)是我们待求的参数集。根据之前我们对于极大似然估计的解释，假设抛开隐变量集不管，我们最终的目的就是根据最终观测到的变量集采用极大似然估计的方法来求解出参数集。所以，我们的目标函数就是最大化似然（这里取似然函数的对数）。

L(Θ|Y,Z)=log P(Y,Z|Θ)L(Θ|Y,Z)=log P(Y,Z|Θ)

如果没有ZZ变量，如上所说，直接可以用极大似然估计的方法来估计参数。但是这里多了一个隐变量ZZ，所以EM算法的精髓思想出来了：

初始化一个Θ0Θ0参数

E步：根据ΘtΘt我们可以计算出ZZ的期望值，记为ZtZt

M步：根据ZtZt我们可以利用极大似然法估计出参数ΘΘ，记为Θt+1Θt+1

重复上述EM步直到收敛

简单阐述就是：其实这里有两类变量，一类是隐变量，一类是待求的参数变量。那么普通的思路该怎么求这个参数变量呢？由上述阐述可以知道，如果我们事先知道了隐变量就能利用极大似然来估计参数，如果我们知道了参数，那么我们可以计算出隐变量集的期望。这里就形成了一个制约，只要我们给出隐变量的初始值就能通过迭代达到两类变量之间的平衡，也就是收敛。类似于我们在生活中的称重，如果要将一类物品分为两部分(比如糖果)，在没有称的情况下，往往我们在左右手进行掂量(这就有点像两类变量)，如果左手上重了就分点到右手上，否则，从右手上扒拉点分到左手，直到感觉两只手上重量差不多。

所以这里就落下了两个最主要的问题：

为什么是求ZZ的期望？

一定会收敛？收敛到哪里？

2.2 算法推导

对于第一个问题，为什么是求ZZ的期望？其实上述只是简单的假设，根据我们的目标需求，需要极大似然估计参数，所以需要知道隐变量，然后采取了这种假设、迭代的思路。实际上EM算法并不是直接求解ZZ的期望，而是将E、M两步联合。

假设迭代进行到第tt步，得到了参数ΘtΘt，这个时候ZZ的概率分布为：P(Z|Y,Θt)P(Z|Y,Θt)。我们不直接计算这个概率分布的期望值，而是计算对数似然函数LL关于ZZ的期望值。同样分为如下两步。

E步(Expectation): 计算对数似然函数LL关于ZZ的期望值（一个条件概率的期望值，已知观测结果YY和参数ΘΘ的条件下，对数似然函数LL的期望值）。这个函数称为QQ函数。

Q(Θ|Θt)=Ez[log P(Y,Z|Θ)|Y,Θt]=∑z{P(Z|Y,Θt) logP(Y,Z|Θ)}(1)(1)(1)Q(Θ|Θt)=Ez[log P(Y,Z|Θ)|Y,Θt](1)=∑z{P(Z|Y,Θt) logP(Y,Z|Θ)}

M步(Maximization):最大化期望似然函数。Θt+1=argmaxΘ Q(Θ|Θt)Θt+1=argmaxΘ Q(Θ|Θt)

重复上述两个步骤，直到收敛到局部最优解。详细的有关收敛问题，可以参考李航老师的《统计学习方法》。

这里就通过简单的方法介绍一下EM算法的核心思路，然后主要是通过以下几个例子来感受一下EM算法。

三、三枚硬币

这里我们首先借用一下李航老师在《统计学习方法》中的三枚硬币模型的例子进行阐述。



Step1: 先定义一些数学变量

Y={y1,y2,y3,........,yn}Y={y1,y2,y3,........,yn}代表最终抛掷硬币的结果，每次的抛掷结果y∈{0,1}y∈{0,1}

Z={z1,z2,z3,.....,zn}Z={z1,z2,z3,.....,zn}表示隐含变量，其实就是A硬币的抛掷结果，所以z∈{0,1}z∈{0,1}

ΘΘ是模型参数，也就是Θ=π,p,qΘ=π,p,q

Step2: 定义整个实验的模型(似然函数)

在进行数学计算之前，模型定义是首要的。上述三硬币的抛掷实验可以用一个概率模型来定义。假设我们只抛掷一次，所以用小写字母表示，xx表示结果和zz隐变量。

P(y|Θ)=P(y,z|Θ)P(y|Θ)=P(y,z|Θ)

因为zz只能取两个值，由条件概率分布，我们展开来看。

P(y|Θ)=P(y,z|Θ)=∑zp(z|Θ)p(y|z,Θ)(2)(3)(2)P(y|Θ)=P(y,z|Θ)(3)=∑zp(z|Θ)p(y|z,Θ)

我们拆开来看，其实两项都是二分布（简单的抛掷硬币过程, 假设A为正面朝上，然后进行一次抛硬币，A反面朝上同样）。所以我们可以继续写。

P(y|Θ)=P(y,z|Θ)=∑zp(z|Θ)p(y|z,Θ)=πpy(1−p)1−y+(1−π)qy(1−q)1−y(4)(5)(6)(4)P(y|Θ)=P(y,z|Θ)(5)=∑zp(z|Θ)p(y|z,Θ)(6)=πpy(1−p)1−y+(1−π)qy(1−q)1−y

我们可以简单的来核对一下这个概率模型写得对不对。我们画出一次抛掷硬币的整个过程，并计算出相应的概率。然后带入到上面的公式中就可以知道模型构建是否正确了。

case1234A(z)1100B10−−C−−10概率π∗pπ∗(1−p)(1−π)∗q(1−π)∗(1−q)caseA(z)BC概率111−π∗p210−π∗(1−p)30−1(1−π)∗q40−0(1−π)∗(1−q)

重复多次的原理也是如此，只不过因为进行的多次独立实验，所以计算概率直接用连乘累积。多次独立实验概率模型如下。由此我们首先得到了似然函数P(Y,Z|Θ)P(Y,Z|Θ)。

P(Y|Θ)=P(Y,Z|Θ)=∏i=1n∑zip(zi|Θ)p(yi|zi,Θ)=∏i=1nπpyi(1−p)1−yi+(1−π)qyi(1−q)1−yi(7)(8)(2)(7)P(Y|Θ)=P(Y,Z|Θ)(8)=∏i=1n∑zip(zi|Θ)p(yi|zi,Θ)(2)=∏i=1nπpyi(1−p)1−yi+(1−π)qyi(1−q)1−yi

这里我们的目标就是求得参数ΘΘ，但是这个似然函数（联乘）求导将非常复杂，所以在极大似然估计中一般都转换为对数似然函数。但是依然非常复杂，所以用EM算法迭代的思想来求解。

Step3：隐变量分布P(Z|Y,Θt)P(Z|Y,Θt)

为了求得QQ函数，下一步我们的目标是得到隐变量的概率分布函数P(Z|Y,Θt)P(Z|Y,Θt)，大家看到这个函数的时候千万不要害怕，其实要从实际实验的角度出发来理解这个公式。这个公式是隐变量ZZ的分布函数，隐变量在实验中其实就是一个0、1值，z∈{0,1}z∈{0,1}。假设我们考虑只进行了一次抛硬币的实验，那么当zz

为1，就代表最后观测结果来自B硬币，否则来自C硬币。所以我们可以拆开来写这个函数。下面假设观测结果来自B硬币，即：A硬币为1，z=1z=1。后面紧随一个抛B硬币的二分布。

μt+1=P(z=1|y,Θt)=πpy(1−p)1−yπpy(1−p)1−y+(1−π)qy(1−q)1−y(9)(9)μt+1=P(z=1|y,Θt)=πpy(1−p)1−yπpy(1−p)1−y+(1−π)qy(1−q)1−y

我们将这个定义为μt+1μt+1，按照之前EM算法的迭代方法可知，μt+1μt+1是根据参数ΘtΘt计算得到。

同理，如果zz为0也是一样的。那么P(Z|Y,Θt)P(Z|Y,Θt) 这个函数就呼之欲出了。这里我们只需要考虑一次实验，zizi.

P(zi|yi,Θt)=P(yi,zi|Θt)∑zP(yi,z|Θt)=⎧⎩⎨⎪⎪⎪⎪πpy(1−p)1−yπpy(1−p)1−y+(1−π)qy(1−q)1−y,(1−π)qy(1−q)1−yπpy(1−p)1−y+(1−π)qy(1−q)1−y,if zi=1if zi=0(10)(3)(10)P(zi|yi,Θt)=P(yi,zi|Θt)∑zP(yi,z|Θt)(3)={πpy(1−p)1−yπpy(1−p)1−y+(1−π)qy(1−q)1−y,if zi=1(1−π)qy(1−q)1−yπpy(1−p)1−y+(1−π)qy(1−q)1−y,if zi=0

Step4: E步，得到QQ函数

由上述理论推导部分可以得到。然后将上述的似然函数(2)(2)和隐变量的分布函数 (3)(3)带入QQ函数(1)(1)中就行。

Q(Θ|Θt)=Ez[log P(Y,Z|Θ)|Y,Θt]=∑z{P(Z|Y,Θt) logP(Y,Z|Θ)}=∑j=1N ∑z P(zj|yj,Θt) log P(yj,zj|Θt)=∑j=1Nμt+1j log(πpy(1−p)1−y)+(1−μt+1j) log ((1−π)qy(1−q)1−y)(11)(12)(13)(4)(11)Q(Θ|Θt)=Ez[log P(Y,Z|Θ)|Y,Θt](12)=∑z{P(Z|Y,Θt) logP(Y,Z|Θ)}(13)=∑j=1N ∑z P(zj|yj,Θt) log P(yj,zj|Θt)(4)=∑j=1Nμjt+1 log(πpy(1−p)1−y)+(1−μjt+1) log ((1−π)qy(1−q)1−y)

Step5: M步,对QQ函数求导，极大似然估计

这里根据Step4我们得到了隐变量的期望（也就是得到了隐变量），由此可以直接对上述的(4)式进行求导，得到相应的参数。

∂Q∂π=(μt+11π−1−μt+111−π)+......+(μt+1Nπ−1−μt+1N1−π)=μt+11−ππ(1−π)+......+μt+1N−ππ(1−π)=0(14)(15)(16)(14)∂Q∂π=(μ1t+1π−1−μ1t+11−π)+......+(μNt+1π−1−μNt+11−π)(15)=μ1t+1−ππ(1−π)+......+μNt+1−ππ(1−π)(16)=0

由此得到 πt+1=1N ∑Nj=1μt+1jπt+1=1N ∑j=1Nμjt+1

同理可得：

pt+1=∑Nj=1 μt+1jyj∑Nj=1 μt+1jpt+1=∑j=1N μjt+1yj∑j=1N μjt+1

qt+1=∑Nj=1 (1−μt+1j)yj∑Nj=1 (1−μt+1j)qt+1=∑j=1N (1−μjt+1)yj∑j=1N (1−μjt+1)

Step6: 进行数值计算并迭代

如何判断停止呢？ 一般是给出一个较小的整数ε1ε1，ε2ε2，若满足如下条件则停止迭代。

||Θt+1−Θt||<ε1or||Q(Θt+1|Θt)−Q(Θt|Θt)||<ε2(17)(18)(17)||Θt+1−Θt||<ε1(18)or||Q(Θt+1|Θt)−Q(Θt|Θt)||<ε2

四、一个简单例子

下面我们将编程实现一个最简单的正态分布参数估计的例子，感受一下EM算法。

case1:

如下图所示是两组一维正态分布数据。这两组是不带隐含变量的正态分布不带隐含变量的正态分布，我们可以很明显的看出这两组正态分布数据，红色的点是一类，蓝色的是另外一类。也可以大概估计出这个例子中两组正态分布的均值，比如红色类别大概是3左右。这就是极大似然估计所处理的一个场景：不带隐变量的参数估计方法.不带隐变量的参数估计方法.



case2:

如下图所示也告诉是两组一维正态分布的数据。但是是带有隐变量的，所以我们完全看不出两个类别，也不太好利用极大似然估计的方法来找到两组参数。这个时候就是EM算法的角斗场，利用反复迭代的思路。利用反复迭代的思路。为了方便理解，我们完全可以理解为用一个滤波器一样的东西在给出的数据上滑动，看哪个滤波器（一组相应的正态分布的参数）能产生最小的误差。



下面我们将按照上述三枚硬币的例子写一小段代码来感受EM算法迭代求解的过程。

Step0：随机数据生成

首先，显然先生成这样两组正态分布的数据。

import numpy as np
from scipy import stats

np.random.seed(110) # for reproducible random results

# set parameters
red_mean = 3
red_std = 0.8

blue_mean = 7
blue_std = 2

# draw 20 samples from normal distributions with red/blue parameters
red = np.random.normal(red_mean, red_std, size=20)
blue = np.random.normal(blue_mean, blue_std, size=20)

# sort all the data for later use
both_colours = np.sort(np.concatenate((red, blue))) # for later use...

我们可以输出结果看看，方便之后与估计的参数进行对比。

>>> np.mean(red)
2.802
>>> np.std(red)
0.871
>>> np.mean(blue)
6.932
>>> np.std(blue)
2.195

Step2: 初始化参数

这里我们的ΘΘ参数就是两组正态分布的参数：均值μ，方差：std均值μ，方差：std

# estimates for the mean
red_mean_guess = 1.1
blue_mean_guess = 9

# estimates for the standard deviation
red_std_guess = 2
blue_std_guess = 1.7

初始化的参数绘制的图像如下所示，看见这张图是不是有点似曾相识，在贝叶斯决策中我们就画过这样的图，判断是否属于某个类别的时候，分界面是一个点，比如下图中，红色和蓝色正态分布图的交叉点就是分界点，小于这个点就是属于红色，否则是蓝色。但是EM算法更加强，不仅能找出这个分界面，而且能估计出参数。



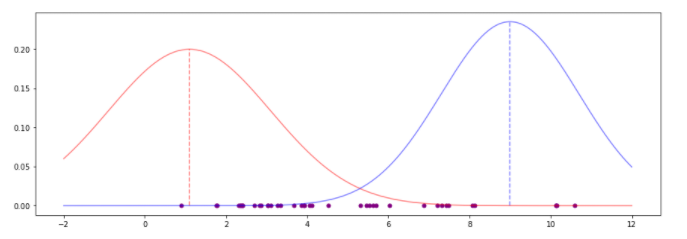
Step2: 计算似然函数

likelihood_of_red = stats.norm(red_mean_guess, red_std_guess).pdf(both_colours)
likelihood_of_blue = stats.norm(blue_mean_guess, blue_std_guess).pdf(both_colours)

likelihood_total = likelihood_of_red + likelihood_of_blue

red_weight = likelihood_of_red / likelihood_total
blue_weight = likelihood_of_blue / likelihood_total

Step3：估计参数

def estimate_mean(data, weight):
return np.sum(data * weight) / np.sum(weight)

def estimate_std(data, weight, mean):
variance = np.sum(weight * (data - mean)**2) / np.sum(weight)
return np.sqrt(variance)

# new estimates for standard deviation
blue_std_guess = estimate_std(both_colours, blue_weight, blue_mean_guess)
red_std_guess = estimate_std(both_colours, red_weight, red_mean_guess)

# new estimates for mean
red_mean_guess = estimate_mean(both_colours, red_weight)
blue_mean_guess = estimate_mean(both_colours, blue_weight)

Step4： 迭代20次后结果

下图是迭代的过程绘制在图像上，可以看出拟合程度。



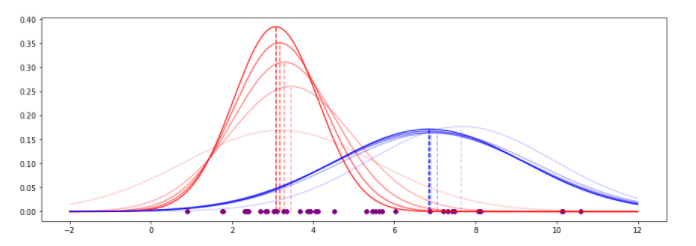
最终的结果图如下所示。分界点大概在4.2左右，参考最开始给出的那个红蓝分解点可以看出，估计还是比较准确的。



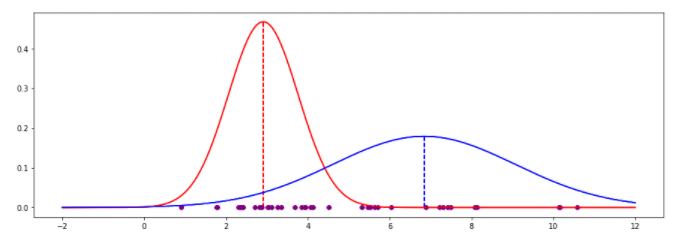
最下面是估计结果参数对比实际的参数的表格。

| EM guess | Actual |  Delta
----------+----------+--------+-------
Red mean  |    2.910 |  2.802 |  0.108
Red std   |    0.854 |  0.871 | -0.017
Blue mean |    6.838 |  6.932 | -0.094
Blue std  |    2.227 |  2.195 |  0.032

参考文献

[1] 李航，《统计学习方法》

[2] 周志华， 《机器学习》

[3] 机器学习算法系列之一】EM算法实例分析

[4] 从最大似然到EM算法浅解

[5] CS229 Lecture notes by Andrew Ng

[6] What is an intuitive explanation of the Expectation Maximization technique?

<个人网页blog已经上线，一大波干货即将来袭：https://faiculty.com/>

/* 版权声明：公开学习资源，只供线上学习，不可转载，如需转载请联系本人 .*/