poj 1737 Connected Graph - 容斥原理 - 动态规划
2018-02-05 15:33
399 查看
Description
An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.
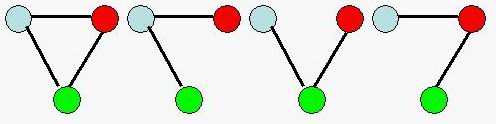
Input
The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero.
Output
For each test case output the answer on a single line.
Sample Input
Sample Output
Source
LouTiancheng@POJ
题目大意
有$n$个互不相同的点,问它们组成的无向连通图的个数。
这一类问题(比如什么连通欧拉图计数,强连通图计数)的常用套路:容斥 + 动归(递推)
直接求并不好求,而且容易出现重复计数的情况。
用$f_{n}$表示我们想要的答案,$g_{n}$表示$n$个点组成的无向图的个数。
显然有$g_{n} = 2^{C_{n}^{2}}$,考虑如何通过$g$来求$f$
我们希望只有1个连通块,所以1号点所在的连通块的大小应为$n$,那么用$g_{n}$减去一号点所在连通块大小不是$n$的图的个数就是$f_{n}$了。
考虑枚举1号点所在连通块的大小为$i$,那么删掉后这个连通块后可以得到一个大小为$(n - i)$的无向图,由于点和点之间互不相同,所以还要考虑选出来的$(i - 1)$的个点的方案数。
所以得到由$g$算$f$的式子:
$f_{n} = g_{n} - \sum_{i = 1}^{n - 1}f_{i}\cdot g_{n - i}\cdot C_{n - 1} ^ {i - 1}$
又因为poj不良心,所以还要写个高精度。
An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.

Input
The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero.
Output
For each test case output the answer on a single line.
Sample Input
1 2 3 4 0
Sample Output
1 1 4 38
Source
LouTiancheng@POJ
题目大意
有$n$个互不相同的点,问它们组成的无向连通图的个数。
这一类问题(比如什么连通欧拉图计数,强连通图计数)的常用套路:容斥 + 动归(递推)
直接求并不好求,而且容易出现重复计数的情况。
用$f_{n}$表示我们想要的答案,$g_{n}$表示$n$个点组成的无向图的个数。
显然有$g_{n} = 2^{C_{n}^{2}}$,考虑如何通过$g$来求$f$
我们希望只有1个连通块,所以1号点所在的连通块的大小应为$n$,那么用$g_{n}$减去一号点所在连通块大小不是$n$的图的个数就是$f_{n}$了。
考虑枚举1号点所在连通块的大小为$i$,那么删掉后这个连通块后可以得到一个大小为$(n - i)$的无向图,由于点和点之间互不相同,所以还要考虑选出来的$(i - 1)$的个点的方案数。
所以得到由$g$算$f$的式子:
$f_{n} = g_{n} - \sum_{i = 1}^{n - 1}f_{i}\cdot g_{n - i}\cdot C_{n - 1} ^ {i - 1}$
又因为poj不良心,所以还要写个高精度。
Code
/**
* poj
* Problem#1737
* Accepted
* Time: 32ms
* Memory: 984k
*/
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef bool boolean;
#define ll long long
typedef class BigInteger {
public:
int w[800];
BigInteger() { }
BigInteger(ll x) {
memset(w, 0, sizeof(w));
while(x) {
w[++w[0]] = x % 10;
x /= 10;
}
}
void clear() {
memset(w, 0, sizeof(w));
}
BigInteger operator + (BigInteger b) {
BigInteger rt;
rt.clear();
rt[0] = max(b[0], w[0]) + 1;
for (int i = 1; i <= rt[0]; i++) {
rt[i] += w[i] + b[i];
rt[i + 1] += rt[i] / 10;
rt[i] %= 10;
}
while (rt[0] && rt[rt[0]] == 0) rt[0]--;
return rt;
}
BigInteger operator - (BigInteger b) {
BigInteger rt;
rt.clear();
rt[0] = w[0];
for (int i = 1; i <= w[0]; i++) {
rt[i] += w[i] - b[i];
if (rt[i] < 0)
rt[i + 1]--, rt[i] += 10;
}
while (rt[0] && rt[rt[0]] == 0) rt[0]--;
return rt;
}
BigInteger operator * (BigInteger b) {
BigInteger rt;
rt.clear();
rt[0] = b[0] + w[0];
for (int i = 1; i <= w[0]; i++)
for (int j = 1; j <= b[0]; j++) {
rt[i + j - 1] += w[i] * b[j];
rt[i + j] += rt[i + j - 1] / 10;
rt[i + j - 1] %= 10;
}
while (rt[0] && rt[rt[0]] == 0) rt[0]--;
return rt;
}
int& operator [] (int pos) {
return w[pos];
}
void print() {
for (int i = w[0]; i; i--)
putchar(w[i] + '0');
putchar('\n');
}
}BigIntegwe;
const int N = 55;
int n;
BigInteger f
, g
;
ll C
;
BigInteger qpow(BigInteger a, ll pos) {
BigInteger rt = 1, pa = a;
for (; pos; pos >>= 1, pa = pa * pa)
if (pos & 1)
rt = rt * pa;
return rt;
}
inline void prepare() {
C[0][0] = 1;
for (int i = 1; i <= 50; i++) {
C[i][0] = C[i][i] = 1;
for (int j = 1; j < i; j++)
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
for (int i = 1; i <= 50; i++) {
f[i] = g[i] = qpow(2, C[i][2]);
for (int j = 1; j < i; j++)
f[i] = f[i] - f[j] * g[i - j] * C[i - 1][j - 1];
}
}
inline boolean init() {
scanf("%d", &n);
return n != 0;
}
inline void solve() {
f
.print();
}
int main() {
prepare();
while(init()) {
solve();
}
return 0;
}
相关文章推荐
- POJ 1737 Connected Graph 高进度+递推
- POJ 1737 Connected Graph 递推
- poj1737 Connected Graph(组合数学)
- POJ 1737 Connected Graph
- poj-1737 Connected Graph[转] ***
- poj 1737 Connected Graph
- POJ 1737: Connected Graph 组合数学 高精度
- 【POJ 1737】Connected Graph
- POJ 1737 Connected Graph 题解(未完成)
- POJ 1737 Connected Graph(JAVA+递推)
- POJ 1737 Connected Graph(组合)
- POJ 1737 Connected Graph 题解(未完成)
- poj 1737 Connected Graph 组合递推计数+高精度
- PKU1737 解题报告 Connected Graph __高精度加法,乘法,减法,组合数
- poj Connected Graph
- POJ 动态规划题目列表
- POJ 1042 钓鱼问题 贪心枚举及动态规划
- POJ 2533 最长上升子序列 [动态规划 + 二分搜索]
- Number of Connected Components in an Undirected Graph
- POJ_2229_Sumsets_(动态规划)
