【量子计算-算法】shor大数分解
2018-01-10 19:58
561 查看
shor大数分解算法




Pick a random number a < N.
Compute gcd(a, N). This may be done using
the Euclidean algorithm.
If gcd(a, N) ≠ 1, then this number is a nontrivial factor
of N, so we are done.
Otherwise, use the period-finding subroutine (below) to find r, the period of
the following function:
f(x)=axmodN,{\displaystyle f(x)=a^{x}{\bmod {N}},}

i.e. the order r{\displaystyle
r}

of a{\displaystyle
a}

in (ZN)×{\displaystyle
(\mathbb {Z} _{N})^{\times }}

,
which is the smallest positive integer r for which f(x+r)=f(x){\displaystyle
f(x+r)=f(x)}

,
or f(x+r)=ax+rmodN≡axmodN.{\displaystyle f(x+r)=a^{x+r}{\bmod {N}}\equiv
a^{x}{\bmod {N}}.}

If r is odd, go back to step 1.
If a r /2 ≡{\displaystyle
\equiv }

−1
(mod N), go back to step 1.
gcd(ar/2 + 1, N) and gcd(ar/2 - 1, N) are
both nontrivial factors of N. We are done.
For example: N=15,a=7,r=4{\displaystyle N=15,a=7,r=4}

, gcd(72±1,15)=gcd(49±1,15){\displaystyle
\mathrm {gcd} (7^{2}\pm 1,15)=\mathrm {gcd} (49\pm 1,15)}

,
where gcd(48,15)=3{\displaystyle \mathrm {gcd} (48,15)=3}

,
and gcd(50,15)=5{\displaystyle \mathrm {gcd} (50,15)=5}

.






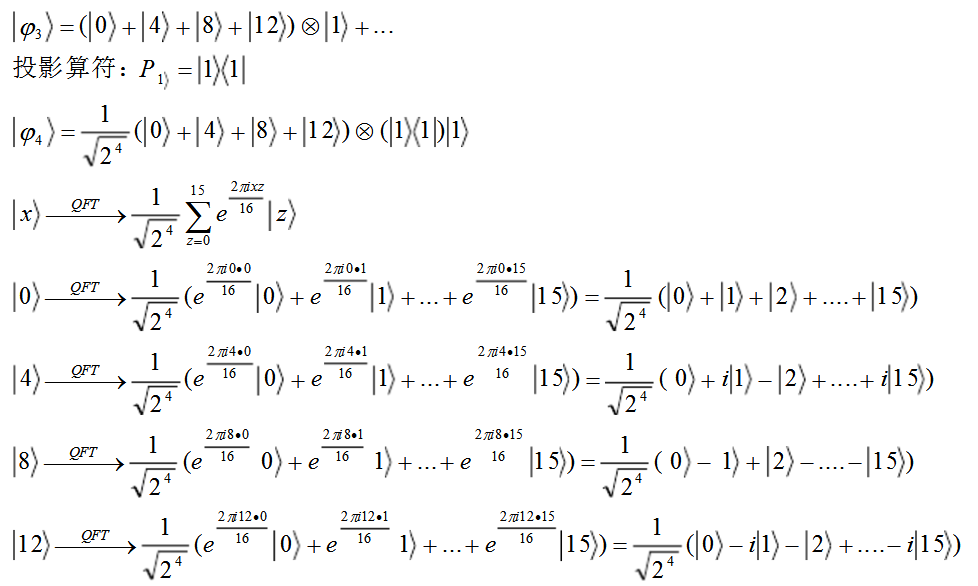

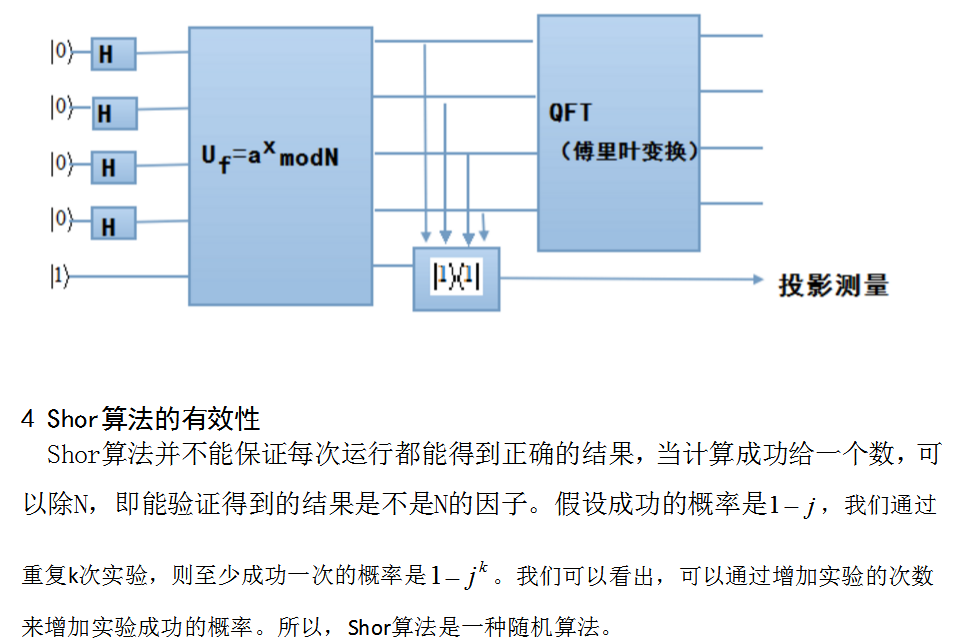
参考文献:
[1] Shor P W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer[M]. Society for Industrial
and Applied Mathematics, 1997.




Classical part[edit]
Pick a random number a < N.Compute gcd(a, N). This may be done using
the Euclidean algorithm.
If gcd(a, N) ≠ 1, then this number is a nontrivial factor
of N, so we are done.
Otherwise, use the period-finding subroutine (below) to find r, the period of
the following function:
f(x)=axmodN,{\displaystyle f(x)=a^{x}{\bmod {N}},}

i.e. the order r{\displaystyle
r}

of a{\displaystyle
a}

in (ZN)×{\displaystyle
(\mathbb {Z} _{N})^{\times }}

,
which is the smallest positive integer r for which f(x+r)=f(x){\displaystyle
f(x+r)=f(x)}

,
or f(x+r)=ax+rmodN≡axmodN.{\displaystyle f(x+r)=a^{x+r}{\bmod {N}}\equiv
a^{x}{\bmod {N}}.}

If r is odd, go back to step 1.
If a r /2 ≡{\displaystyle
\equiv }

−1
(mod N), go back to step 1.
gcd(ar/2 + 1, N) and gcd(ar/2 - 1, N) are
both nontrivial factors of N. We are done.
For example: N=15,a=7,r=4{\displaystyle N=15,a=7,r=4}

, gcd(72±1,15)=gcd(49±1,15){\displaystyle
\mathrm {gcd} (7^{2}\pm 1,15)=\mathrm {gcd} (49\pm 1,15)}

,
where gcd(48,15)=3{\displaystyle \mathrm {gcd} (48,15)=3}

,
and gcd(50,15)=5{\displaystyle \mathrm {gcd} (50,15)=5}

.






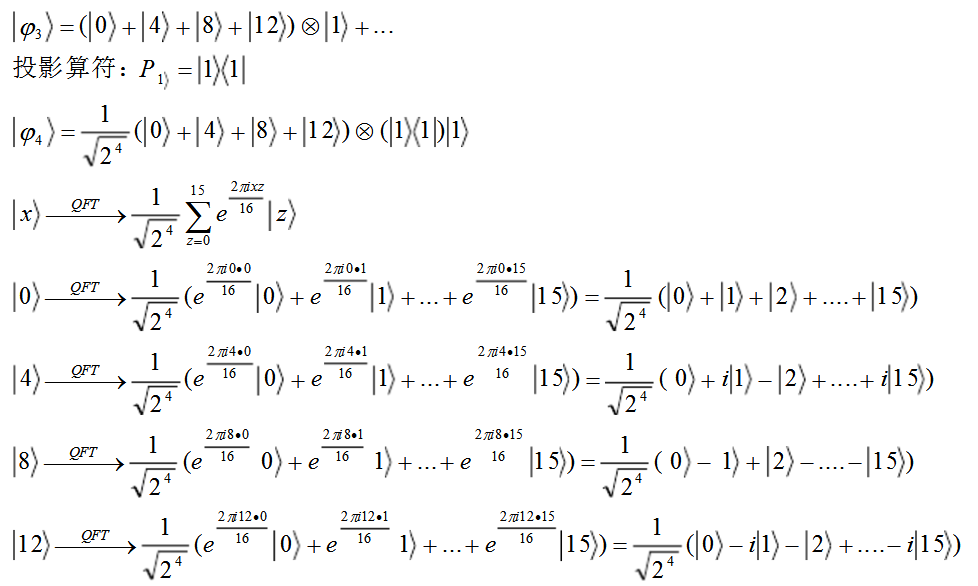


参考文献:
[1] Shor P W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer[M]. Society for Industrial
and Applied Mathematics, 1997.
相关文章推荐
- 量子计算核心突破!Shor算法实现或使密码成摆设
- 量子计算核心突破!Shor算法实现或使密码成摆设
- 一种计算大数阶乘的算法
- 基于矩阵分解的推荐算法-梯度下降算法-非并行计算[转载]
- 一种计算大数阶乘的算法
- 【知识点】大数分解与素数判定 --- 【Miller-rabin算法】【pollard-rho算法】
- 一步一步写算法(之大数计算)
- 算法 - RSA大数分解
- WV.30-大数阶乘算法10-用Stirling逼近近似计算阶乘的探讨与应用
- 算法学习之一(二):矩阵计算——LU分解
- 算法 大数计算:加减乘除,模,阶乘,进制转换(大数除法取余)
- poj 1845(快速幂+二分计算等比数列和+大数因子分解+因子和计算+模除溢出)
- 如何解读「量子计算应对大数据挑战:中国科大首次实现量子机器学习算法」?——是KNN算法吗?
- 一步一步写算法(之大数计算)
- 数学#素数判定Miller_Rabin+大数因数分解Pollard_rho算法 POJ 1811&2429
- WV.23-大数阶乘算法3-近似计算之一
- Miller_raibin算法随机化检测素数 & Pollar_rho 算法分解大数
- WV.24-大数阶乘算法4-近似计算之二
- 一步一步写算法(之大数计算)
- 素数判别和大数分解
