codeforces 901B GCD of Polynomials (数论+构造)
2017-12-21 11:27
591 查看
B. GCD of Polynomials
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Suppose you have two polynomials

and
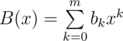
.
Then polynomial
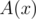
can
be uniquely represented in the following way:
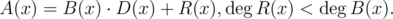
This can be done using long division. Here,
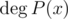
denotes
the degree of polynomial P(x).
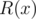
is
called the remainder of division of polynomial
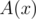
by
polynomial
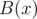
,
it is also denoted as

.
Since there is a way to divide polynomials with remainder, we can define Euclid's algorithm of finding the greatest common divisor of two polynomials. The algorithm takes two polynomials
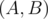
.
If the polynomial
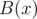
is
zero, the result is
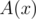
,
otherwise the result is the value the algorithm returns for pair

.
On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
You are given an integer n. You have to build two polynomials with degrees not greater than n,
such that their coefficients are integers not exceeding 1 by their absolute value, the leading coefficients (ones with the greatest power of x)
are equal to one, and the described Euclid's algorithm performs exactly n steps finding their greatest common divisor. Moreover, the degree of the first
polynomial should be greater than the degree of the second. By a step of the algorithm we mean the transition from pair
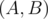
to
pair

.
Input
You are given a single integer n (1 ≤ n ≤ 150) —
the number of steps of the algorithm you need to reach.
Output
Print two polynomials in the following format.
In the first line print a single integer m (0 ≤ m ≤ n) —
the degree of the polynomial.
In the second line print m + 1 integers between - 1 and 1 —
the coefficients of the polynomial, from constant to leading.
The degree of the first polynomial should be greater than the degree of the second polynomial, the leading coefficients should be equal to 1.
Euclid's algorithm should perform exactly n steps when called using these polynomials.
If there is no answer for the given n, print -1.
If there are multiple answer, print any of them.
Examples
input
output
input
output
Note
In the second example you can print polynomials x2 - 1 and x.
The sequence of transitions is
(x2 - 1, x) → (x, - 1) → ( - 1, 0).
There are two steps in it.
//gcd(a*x+b,a)=gcd(a,b)
//因为 b的x最高次小于a 并且逆推的话 前一项是符合系数在[-1,1]
// 那么 a*x相当于 <<1
// gcd (a*x+b,a)=gcd(a*x-b,a)
(a,b)从(1,0)倒推,每次a*x+b或者 a*x-b得到下一项 (a*x+/- b,a)重复这个操作
AC代码:
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Suppose you have two polynomials

and
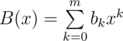
.
Then polynomial
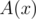
can
be uniquely represented in the following way:
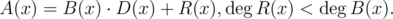
This can be done using long division. Here,
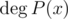
denotes
the degree of polynomial P(x).
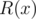
is
called the remainder of division of polynomial
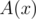
by
polynomial
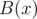
,
it is also denoted as

.
Since there is a way to divide polynomials with remainder, we can define Euclid's algorithm of finding the greatest common divisor of two polynomials. The algorithm takes two polynomials
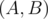
.
If the polynomial
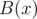
is
zero, the result is
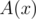
,
otherwise the result is the value the algorithm returns for pair

.
On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
You are given an integer n. You have to build two polynomials with degrees not greater than n,
such that their coefficients are integers not exceeding 1 by their absolute value, the leading coefficients (ones with the greatest power of x)
are equal to one, and the described Euclid's algorithm performs exactly n steps finding their greatest common divisor. Moreover, the degree of the first
polynomial should be greater than the degree of the second. By a step of the algorithm we mean the transition from pair
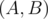
to
pair

.
Input
You are given a single integer n (1 ≤ n ≤ 150) —
the number of steps of the algorithm you need to reach.
Output
Print two polynomials in the following format.
In the first line print a single integer m (0 ≤ m ≤ n) —
the degree of the polynomial.
In the second line print m + 1 integers between - 1 and 1 —
the coefficients of the polynomial, from constant to leading.
The degree of the first polynomial should be greater than the degree of the second polynomial, the leading coefficients should be equal to 1.
Euclid's algorithm should perform exactly n steps when called using these polynomials.
If there is no answer for the given n, print -1.
If there are multiple answer, print any of them.
Examples
input
1
output
10 10
1
input
2
output
2-1 0 110 1
Note
In the second example you can print polynomials x2 - 1 and x.
The sequence of transitions is
(x2 - 1, x) → (x, - 1) → ( - 1, 0).
There are two steps in it.
//gcd(a*x+b,a)=gcd(a,b)
//因为 b的x最高次小于a 并且逆推的话 前一项是符合系数在[-1,1]
// 那么 a*x相当于 <<1
// gcd (a*x+b,a)=gcd(a*x-b,a)
(a,b)从(1,0)倒推,每次a*x+b或者 a*x-b得到下一项 (a*x+/- b,a)重复这个操作
AC代码:
#include<bits/stdc++.h>
using namespace std;
struct node
{
int p[200];
void q() //*x
{
for(int i=151;i>0;i--)
p[i]=p[i-1];
p[0]=0;
}
void f(int a[]) //+a
{
for(int i=0;i<=150;i++)
{
p[i]+=a[i];
}
}
void g(int a[]) //-2*a
{
for(int i=0;i<=150;i++)
{
p[i]-=2*a[i];
}
}
bool vj()
{
bool flag=true;
for(int i=0;i<=150;i++)
{
if(p[i]>1||p[i]<-1)
{
flag=false;
break;
}
}
return flag;
}
};
int main()
{
int n;
scanf("%d",&n);
int m=n;
int ans1[200][200];
int ans2[200][200];
node a,b;
memset(a.p,0,sizeof(a.p));
memset(b.p,0,sizeof(b.p));
memset(ans2,0,sizeof(ans2));
a.p[0]=1;
memset(ans1,0,sizeof(ans1));
ans1[0][0]=1;
int tt=1;
while(m--)
{
int t[200];
for(int i=0;i<tt;i++)
{
t[i]=a.p[i];
}
a.q();
a.f(b.p);
if(!a.vj())
{
a.g(b.p);
}
for(int i=0;i<=tt;i++)
{
ans1[tt][i]=a.p[i];
ans2[tt][i]=t[i];
b.p[i]=t[i];
}
tt++;
}
printf("%d\n",n);
for(int i=0;i<=n;i++)
printf("%d%c",ans1[i],i==n?'\n':' ');
printf("%d\n",n-1);
for(int i=0;i<=n-1;i++)
printf("%d%c",ans2[i],(i==(n-1))?'\n':' ');
}
相关文章推荐
- codeforces 222C C. Reducing Fractions(数论+构造)
- CodeForces 45 G.Prime Problem(构造+数论)
- codeforces 66D D. Petya and His Friends( 数论+构造)
- codeforces 487C C. Prefix Product Sequence(数论+构造)
- codeforces 225B B. Well-known Numbers(数论+二分+贪心+构造)
- codeforces 201A A. Clear Symmetry(数论+构造)
- Codeforces 716C[数论][构造]
- codeforces 449C C. Jzzhu and Apples(数论+构造)
- [数论][构造][离散对数] Codeforces 913 G. Power Substring
- codeforces 121C C. Lucky Permutation(数论+构造)
- codeforces 487C C. Prefix Product Sequence(构造+数论)
- codeforces 123A A. Prime Permutation(数论+构造)
- Codeforces 584 A. Olesya and Rodion 数论+找规律(构造)
- CodeForces 66 D.Petya and His Friends(构造+数论+高精度)
- CodeForces 449 C.Jzzhu and Apples(构造+数论)
- codeforces 901B GCD of Polynomials
- Codeforces 303A 构造+数论
- codeforces 113C C. Double Happiness(数论+暴力)
- codeforces 897B. Chtholly's request(思维or构造)
- 【Codeforces 631 B Print Check 】+ 简单构造
