[2017纪中11-2]救赎 dfs序+树状数组 / 递推
2017-11-02 19:29
351 查看
题面
考场O(nlogn)做法:
4000
对于一棵有根树,考虑每个点和它的儿子们的那些边的期望,容易得出答案为:
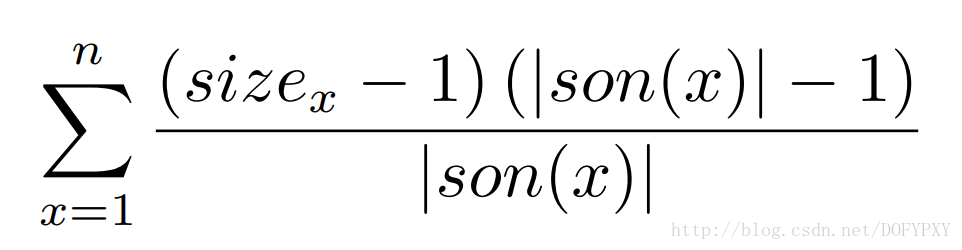
假如建出来的树以1为根,计算出子树大小sz和儿子个数num,那么考虑一个点对不同点为根节点的答案的贡献:
1、根节点不在它的子树中,上式size=sz[x],|son|=num[x]。
2、根节点为它自己,上式size=n,|son|=num[x]+1。
3、根节点在它的某个儿子p的子树中,上式size=n-sz[p],|son|=num[x]。
在计算1的答案时上面的结论会有一些偏差,特判一下。
我们发现对于每种情况内部,这个点贡献是相同的,不难发现每种情况都是在dfs序上连续的一段或两段,树状数组维护一下区间加即可。
代码:
正解O(n)做法:
考虑当前已经计算出x的父亲fa为根的答案,我们要递推出x为根的答案。就像splay那样单旋一样,只有x和fa的size和|son|发生了改变,减去原来的贡献再加上新的贡献即可。
还有一些O(n)预处理逆元的技巧。。。
代码:
考场O(nlogn)做法:
4000
对于一棵有根树,考虑每个点和它的儿子们的那些边的期望,容易得出答案为:
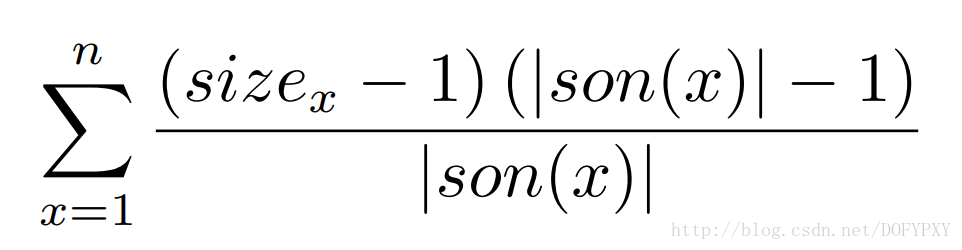
假如建出来的树以1为根,计算出子树大小sz和儿子个数num,那么考虑一个点对不同点为根节点的答案的贡献:
1、根节点不在它的子树中,上式size=sz[x],|son|=num[x]。
2、根节点为它自己,上式size=n,|son|=num[x]+1。
3、根节点在它的某个儿子p的子树中,上式size=n-sz[p],|son|=num[x]。
在计算1的答案时上面的结论会有一些偏差,特判一下。
我们发现对于每种情况内部,这个点贡献是相同的,不难发现每种情况都是在dfs序上连续的一段或两段,树状数组维护一下区间加即可。
代码:
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int maxn=100010;
const int mod=998244353;
int n,dfn[maxn],tim,num[maxn],sz[maxn],c[maxn],bg[maxn],ed[maxn];
struct edge
{
int t;
edge *next;
}*con[maxn];
ll ksm(ll a,int b){ll r=1;for(;b;b>>=1){if(b&1)r=r*a%mod; a=a*a%mod;} return r;}
void add(ll x,ll d){for(;x<=n;x+=(x&(-x))) c[x]=(c[x]+d)%mod;}
ll qry(ll x) {ll r=0;for(;x>0;x-=(x&(-x))) r=(r+c[x])%mod; return r;}
void mdf(int l,int r,ll d){if(l<=r) add(l,d),add(r+1,mod-d);}
void ins(int x,int y)
{
edge *p=new edge;
p->t=y;
p->next=con[x];
con[x]=p;
}
void dfs(int v,int fa)
{
dfn[++tim]=v;
bg[v]=tim;
sz[v]=1;num[v]=0;
for(edge *p=con[v];p;p=p->next)
if(p->t!=fa)
{
dfs(p->t,v);
sz[v]+=sz[p->t];
num[v]++;
}
ed[v]=tim;
}
void cal(int v,int fa)
{
ll inv=ksm(num[v],mod-2);
if(num[v]!=0)
{
ll tmp=inv*(sz[v]-1)%mod*(num[v]-1)%mod;
mdf(1,bg[v]-1,tmp);
mdf(ed[v]+1,n,tmp);
}
mdf(bg[v],bg[v],ksm(num[v]+(fa>0),mod-2)*(n-1)%mod*(num[v]-(fa==0))%mod);
if(fa==0) inv=ksm(num[v]-1,mod-2);
for(edge *p=con[v];p;p=p->next)
if(p->t!=fa)
{
mdf(bg[p->t],ed[p->t],inv*(n-sz[p->t]-1)%mod*(num[v]-1-(fa==0))%mod);
cal(p->t,v);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n-1;i++)
{
int x,y;
scanf("%d%d",&x,&y);
ins(x,y);
ins(y,x);
}
dfs(1,0);
cal(1,0);
for(int i=1;i<=n;i++)
printf("%lld\n",qry(bg[i]));
return 0;
}正解O(n)做法:
考虑当前已经计算出x的父亲fa为根的答案,我们要递推出x为根的答案。就像splay那样单旋一样,只有x和fa的size和|son|发生了改变,减去原来的贡献再加上新的贡献即可。
还有一些O(n)预处理逆元的技巧。。。
代码:
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int maxn=100010;
const int mod=998244353;
int n,num[maxn],sz[maxn];
ll inv[maxn],jie[maxn],ans[maxn];
struct edge
{
int t;
edge *next;
}*con[maxn];
ll ksm(ll a,int b){ll r=1;for(;b;b>>=1){if(b&1)r=r*a%mod; a=a*a%mod;} return r;}
void ins(int x,int y)
{
edge *p=new edge;
p->t=y;
p->next=con[x];
con[x]=p;
}
void dfs(int v,int fa)
{
sz[v]=1;num[v]=0;
for(edge *p=con[v];p;p=p->next)
if(p->t!=fa)
{
dfs(p->t,v);
sz[v]+=sz[p->t];
num[v]++;
}
}
ll G(int z,int m)
{
return inv[m]*(z-1)%mod*(m-1)%mod;
}
void cal(int v,int fa)
{
for(edge *p=con[v];p;p=p->next)
if(p->t!=fa)
{
ans[p->t]=(ans[v]-G(sz[p->t],num[p->t])-G(n,num[v]+(fa>0))+G(n,num[p->t]+1)+G(n-sz[p->t],num[v]+(fa>0)-1)+mod*2)%mod;
cal(p->t,v);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n-1;i++)
{
int x,y;
scanf("%d%d",&x,&y);
ins(x,y);
ins(y,x);
}
jie[0]=1;
for(int i=1;i<=n;i++) jie[i]=jie[i-1]*i%mod;
inv
=ksm(jie
,mod-2);
for(int i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
for(int i=1;i<=n;i++) inv[i]=jie[i-1]*inv[i]%mod;
dfs(1,0);
for(int i=1;i<=n;i++)
ans[1]=(ans[1]+G(sz[i],num[i]))%mod;
cal(1,0);
for(int i=1;i<=n;i++)
printf("%lld\n",ans[i]);
return 0;
}
相关文章推荐
- [2017纪中11-6]拆网线 树型DP/二分图匹配
- [2017纪中11-8]购物 贪心+优先队列
- [2017纪中11-8]好文章 字符串hash+STL
- [2017纪中11-9]乘积 数论+分组背包
- [递推] Codeforces 660E Educational Codeforces Round 11 E. Different Subsets For All Tuples
- [2017纪中11-6]奇怪的队列 树状数组+二分/线段树
- [2017纪中11-9]道路重建 点双连通分量+树的直径
- [2017纪中11-9]玩游戏 最短路数+LCA 4000
- [2017纪中10-25]嘟噜噜 约瑟夫问题 递推
- [2017纪中11-4][Codeforces Round #395 Div.1]C pacifist
- [2017纪中11-4][ARC071]F-neutral DP
- [2017纪中11-5]轰炸 强联通分量+DAG最长路
- [2017纪中11-2]字典序 拓扑排序+优先队列
- [2017纪中11-5]好路线 DP
- [2017纪中11-3][ARC069-F]高考是不可能高考的 2-sat+线段树优化建图
- [2017纪中11-5]仔细的检查 树hash
- [2017纪中11-2]失格 最小生成树+数论
- [2017纪中11-3]机房比教室好多了 博弈+树型DP
- [2017纪中11-1]背包 二分
- test 11-8(Canceled) T2[递推 矩阵快速幂]
