HDU 1402 A * B Problem Plus（FFT）

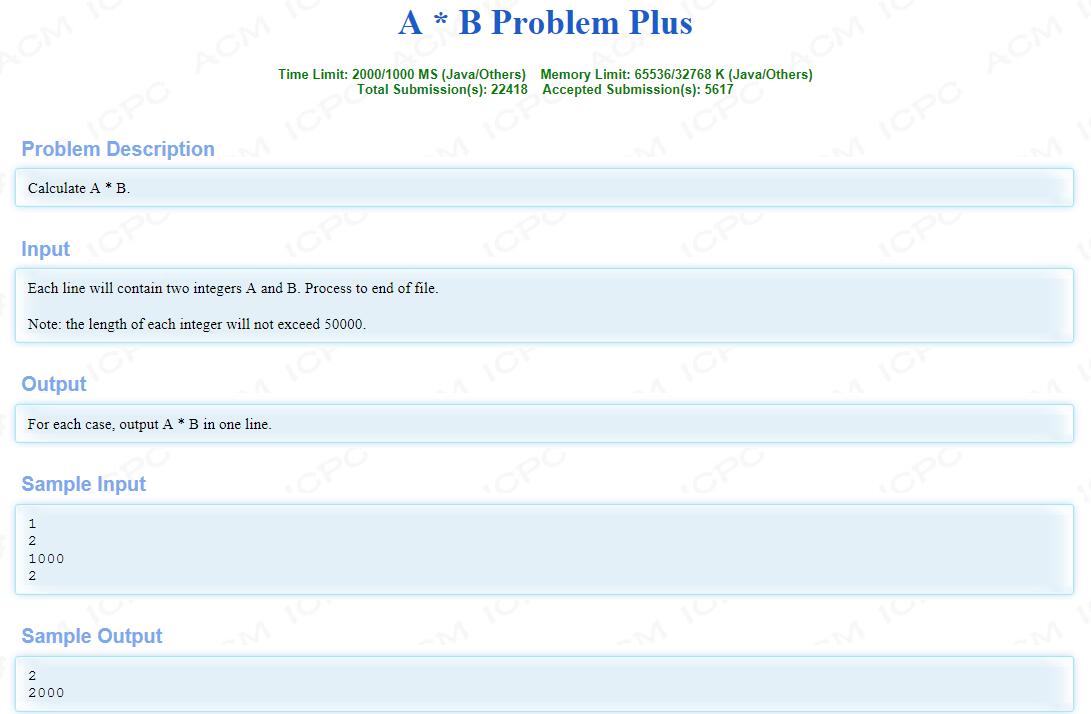
题解：题意很简单，但是我们采用大数乘法的话复杂度是O(n^2)，一定会超时的。

因此需要想一个更优的方法，也就是FFT了。这里就简要介绍一下了（理解不算太透彻）

叉解的FFT讲解：https://wenku.baidu.com/view/20c234cf581b6bd97f19eaea.html

大佬的FFT讲解：http://blog.csdn.net/acdreamers/article/details/39005227

FFT（快速傅里叶变换）在信息学的应用极为广泛，其中重要的一项应用便是求解多项式，因为

普通的多项式求解的复杂度是N^2,大多数时候无法满足需要，因此我们迫切需要一种更快的求解方式。

也就出现了FFT，关于系数表示法这里不再多讲，详情看上两个链接即可。

我就说一下具体的求解步骤，在了解了多项式的点值表示法后，我们需要选择n个点作为求值点

这n个点不能随便选，否则仍然不能降低复杂度，而是选择n次单位复根，为什么这样选？


次单位复根是满足

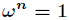
的复数

，

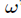
次单位复根恰好有

个，它们是

，

，

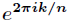
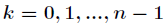
为了解释这一式子，利用复数幂的定义

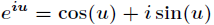
，值

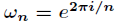
称为主

次单位根，

所有其它

次单位复根都是

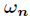
的

次幂。

 

n个

次单位复根

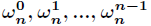
在乘法运算下形成一个群，该群的结构与加法群

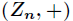
模

相同。

 

    接下来认识几个关于

次单位复根的重要性质。

   

    （1）相消引理

 

        对于任何整数

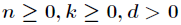
，有


 

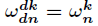
    （2）折半引理

 

        如果

且为偶数，则


 

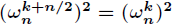
    （3）求和引理

 

        对任意整数

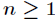
和不能被

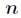
整除的非零整数

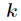
，有

 

          


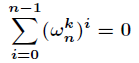
我们利用的就是n次单位复根的折半引理。。





这样原本的多项式便一分为二，剩下的就是分治的思想了，

由于在奇偶分类时导致顺序发生变化，所以需要先通过Rader算法进行倒位序，

然后通过蝴蝶操作可以将前半部分和后半部分的值求出。。。
总时间复杂度O(nlog(n))... 因为没有完全理解，讲解有些问题，日后慢慢补充。。。
模板参考：http://www.cnblogs.com/kuangbin/archive/2013/07/24/3210389.html

#include<math.h>
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
using namespace std;
const double PI = acos(-1.0);
#define maxn 200010
struct complex
{
double r,i;
complex(double _r=0.0,double _i=0.0)
{
r=_r;i=_i;
}
complex operator +(const complex &b)
{
return complex(r+b.r,i+b.i);
}
complex operator -(const complex &b)
{
return complex(r-b.r,i-b.i);
}
complex operator *(const complex &b)
{
return complex(r*b.r-i*b.i,r*b.i+i*b.r);
}
};
/*
* 进行FFT和IFFT前的反转变换。
* 位置i和 （i二进制反转后位置）互换
* len必须取2的幂
*/
complex x1[maxn],x2[maxn];
char str1[maxn],str2[maxn];
int sum[maxn];
//雷德算法--倒位序
void change(complex y[],int len)
{
int i,j,k;
for(i=1,j=len/2;i<len-1;i++)
{
if(i<j)
swap(y[i],y[j]);
//交换互为小标的元素，i<j保证只交换一次
//i做正常的+1，j左反转类型的+1,始终保持i和j是反转的
k=len/2;
while(j>=k)
j-=k,k/=2;
if(j<k)
j+=k;
}
}
/*
* 做FFT
* len必须为2^k形式，
* on==1时是DFT，on==-1时是IDFT
*/
void fft(complex y[],int len,int on)
{
change(y,len);
for(int h=2;h<=len;h<<=1)//分治后计算长度为h的DFT
{
complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));//单位复根e^(2*PI/m)用欧拉公式展开
for(int j=0;j<len;j+=h)
{
complex w(1,0);//旋转因子
for(int k=j;k<j+h/2;k++)
{
complex u=y[k];
complex t=w*y[k+h/2];
y[k]=u+t;//蝴蝶合并操作
y[k+h/2]=u-t;
w=w*wn;//更新旋转因子
}
}
}
if(on == -1)
for(int i = 0;i < len;i++)
y[i].r /= len;
}
int main(void)
{
while(scanf("%s%s",str1,str2)!=EOF)
{
int len1=strlen(str1);
int len2=strlen(str2);
int len=1;
while(len<len1*2 || len<len2*2)
len<<=1;
for(int i=0;i<len1;i++)
x1[i]=complex(str1[len1-1-i]-'0',0);
for(int i=len1;i<len;i++)
x1[i]=complex(0,0);
for(int i=0;i<len2;i++)
x2[i]=complex(str2[len2-1-i]-'0',0);
for(int i=len2;i<len;i++)
x2[i]=complex(0,0);
fft(x1,len,1);fft(x2,len,1);//求DFT
for(int i=0;i<len;i++)
x1[i]=x1[i]*x2[i];
fft(x1,len,-1);//求IDFT
for(int i=0;i<len;i++)
sum[i]=(int)(x1[i].r+0.5);
for(int i=0;i<len;i++)
{
sum[i+1]+=sum[i]/10;
sum[i]%=10;
}
len=len1+len2-1;
while(sum[len]<=0 && len>0)
len--;
for(int i=len;i>=0;i--)
printf("%c",sum[i]+'0');
printf("\n");
}
return 0;
}