算法简介
2017-10-12 15:54
316 查看
算法是解决问题的方法和过程!
算法主要分为一下几类:
1、贪心算法
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。
举例如下:
(1)活动选择问题
这是《算法导论》上的例子,也是一个非常经典的问题。有n个需要在同一天使用同一个教室的活动a1,a2,…,an,教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后,活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠,ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。例如下图所示的活动集合S,其中各项活动按照结束时间单调递增排序。
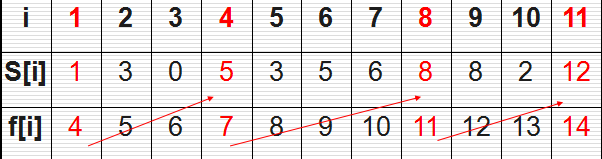
考虑使用贪心算法的解法。为了方便,我们用不同颜色的线条代表每个活动,线条的长度就是活动所占据的时间段,蓝色的线条表示我们已经选择的活动;红色的线条表示我们没有选择的活动。
如果我们每次都选择开始时间最早的活动,不能得到最优解:

如果我们每次都选择持续时间最短的活动,不能得到最优解:

可以用数学归纳法证明,我们的贪心策略应该是每次选取结束时间最早的活动。直观上也很好理解,按这种方法选择相容活动为未安排活动留下尽可能多的时间。这也是把各项活动按照结束时间单调递增排序的原因。
(2)钱币找零问题
这个问题在我们的日常生活中就更加普遍了。假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元,至少要用多少张纸币?用贪心算法的思想,很显然,每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。在程序中已经事先将Value按照从小到大的顺序排好。
2、动态规划算法
当最优化问题具有重复子问题和最优子结构的时候,就是动态规划出场的时候了。动态规划算法的核心就是提供了一个memory来缓存重复子问题的结果,避免了递归的过程中的大量的重复计算。动态规划算法的难点在于怎么将问题转化为能够利用动态规划算法来解决。当重复子问题的数目比较小时,动态规划的效果也会很差。如果问题存在大量的重复子问题的话,那么动态规划对于效率的提高是非常恐怖的。
先看下面的例子:
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元?
我们凭直观感觉告诉自己,先选面值最大,因此最多选2枚5元的硬币,现在是10元了,还差一元,接下来我们挑选第二大的3元硬币,发现不行(10+3=13超了),因此我们继续选第三大的硬币也就是1元硬币,选一个就可以(10+1=11),所以总共用了3枚硬币凑够了11元。这就是贪心法,每次选最大的。但是我们将面值改为2元,3元和5元的硬币,再用贪心法就不行了。为什么呢?按照贪心思路,我们同样先取2枚最大5元硬币,现在10元了,还差一元,接下来选第二大的,发现不行,再选第三大的,还是不行,这时用贪心方法永远凑不出11元,但是你仔细看看,其实我们可以凑出11元的,2枚3元硬币和1枚五元硬币就行了,这是人经过思考判断出来了的,但是怎么让计算机算出来呢?这就要用动态规划的思想。
因此,可得贪心算法与动态规划算法的区别:
贪心算法:
1.贪心算法中,作出的每步贪心决策都无法改变,因为贪心策略是由上一步的最优解推导下一步的最优解,而上一部之前的最优解则不作保留。
2.由(1)中的介绍,可以知道贪心法正确的条件是:每一步的最优解一定包含上一步的最优解。
动态规划算法:
1.全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有最优解
2.动态规划的关键是状态转移方程,即如何由以求出的局部最优解来推导全局最优解
3.边界条件:即最简单的,可以直接得出的局部最优解
举例如下:
例1:台阶问题
有n级台阶,一个人每次上一级或者两级,问有多少种走完n级台阶的方法。
分析:动态规划的实现的关键在于能不能准确合理的用动态规划表来抽象出 实际问题。在这个问题上,我们让f(n)表示走上n级台阶的方法数。
那么当n为1时,f(n) = 1,n为2时,f(n) =2,就是说当台阶只有一级的时候,方法数是一种,台阶有两级的时候,方法数为2。那么当我们要走上n级台阶,必然是从n-1级台阶迈一步或者是从n-2级台阶迈两步,所以到达n级台阶的方法数必然是到达n-1级台阶的方法数加上到达n-2级台阶的方法数之和。即f(n) = f(n-1)+f(n-2),我们用dp
来表示动态规划表,dp[i],i>0,i<=n,表示到达i级台阶的方法数。
例2:0-1背包问题
01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >
f[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包中,可以取得的最大价值。
Pi表示第i件物品的价值。
决策:为了背包中物品总价值最大化,第 i件物品应该放入背包中吗 ?
题目描述:
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
只要你能通过找规律手工填写出上面这张表就算理解了01背包的动态规划算法。
首先要明确这张表是至底向上,从左到右生成的。
为了叙述方便,用e2单元格表示e行2列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了。
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品e,d都不是这个背包能装的。
同理,c2=0,b2=3,a2=6。
总结,由上两例可以看出,动态规划算法的基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解
[b]3、分治算法
[/b]
分治算法的逻辑更简单了,就是一个词,分而治之。分治算法就是把一个大的问题分为若干个子问题,然后在子问题继续向下分,一直到base cases,通过base cases的解决,一步步向上,最终解决最初的大问题。
当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。这就是分治策略的基本思想。
[b]4、回溯算法[/b]
回溯算法是深度优先策略的典型应用,回溯算法就是沿着一条路向下走,如果此路不同了,则回溯到上一个
分岔路,在选一条路走,一直这样递归下去,直到遍历万所有的路径。八皇后问题是回溯算法的一个经典问题,还有一个经典的应用场景就是迷宫问题。
例1、八皇后问题
对于八皇后的求解可采用回溯算法,从上至下依次在每一行放置皇后,进行搜索,若在某一行的任意一列放置皇后均不能满足要求,则不再向下搜索,而进行回溯,回溯至有其他列可放置皇后的一行,再向下搜索,直到搜索至最后一行,找到可行解,输出。
可以使用递归函数实现上述回溯算法,递归函数用于求解在某一行放置皇后,具体代码如下所示。
代码
#include <stdlib.h>
#include <stdio.h>
int m[8][8] = {0};//表示棋盘,初始为0,表示未放置皇后
int num = 0;//解数目
//对于棋盘前row-1行已放置好皇后
//检查在第row行、第column列放置一枚皇后是否可行
bool check(int row,int column)
{
if(row==1) return true;
int i,j;
//纵向只能有一枚皇后
for(i=0;i<=row-2;i++)
{
if(m[i][column-1]==1) return false;
}
//左上至右下只能有一枚皇后
i = row-2;
j = i-(row-column);
while(i>=0&&j>=0)
{
if(m[i][j]==1) return false;
i--;
j--;
}
//右上至左下只能有一枚皇后
i = row-2;
j = row+column-i-2;
while(i>=0&&j<=7)
{
if(m[i][j]==1) return false;
i--;
j++;
}
return true;
}
//当已放置8枚皇后,为可行解时,输出棋盘
void output()
{
int i,j;
num++;
printf("answer %d:\n",num);
for(i=0;i<8;i++)
{
for(j=0;j<8;j++) printf("%d ",m[i][j]);
printf("\n");
}
}
//采用递归函数实现八皇后回溯算法
//该函数求解当棋盘前row-1行已放置好皇后,在第row行放置皇后
void solve(int row)
{
int j;
//考虑在第row行的各列放置皇后
for (j=0;j<8;j++)
{
//在其中一列放置皇后
m[row-1][j] = 1;
//检查在该列放置皇后是否可行
if (check(row,j+1)==true)
{
//若该列可放置皇后,且该列为最后一列,则找到一可行解,输出
if(row==8) output();
//若该列可放置皇后,则向下一行,继续搜索、求解
else solve(row+1);
}
//取出该列的皇后,进行回溯,在其他列放置皇后
m[row-1][j] = 0;
}
}
//主函数
int main()
{
//求解八皇后问题
solve(1);
return 0;
}
[b]5、分支限界算法[/b]
回溯算法是深度优先,那么分支限界法就是广度优先的一个经典的例子。回溯法一般来说是遍历整个解空间,获取问题的所有解,而分支限界法则是获取一个解(一般来说要获取最优解)。
例1、旅行商问题
省略
6、迭代法
迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法,即一次性解决问题。迭代法又分为精确迭代和近似迭代。“二分法”和“牛顿迭代法”属于近似迭代法。迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
举例1
一个饲养场引进一只刚出生的新品种兔子,这种兔子从出生的下一个月开始,每月新生一只兔子,新生的兔子也如此繁殖。如果所有的兔子都不死去,问到第 12 个月时,该饲养场共有兔子多少只?
分析:这是一个典型的递推问题。我们不妨假设第 1 个月时兔子的只数为 u 1 ,第 2 个月时兔子的只数为 u 2 ,第 3 个月时兔子的只数为 u 3 ,……根据题意,“这种兔子从出生的下一个月开始,每月新生一只兔子”,则有
u 1 = 1 , u 2 = u 1 + u 1 × 1 = 2 , u 3 = u 2 + u 2 × 1 = 4 ,……
根据这个规律,可以归纳出下面的递推公式:
u n = u(n - 1)× 2 (n ≥ 2)。这样就可递推出第12个月时兔子的总数量。
算法主要分为一下几类:
1、贪心算法
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。
举例如下:
(1)活动选择问题
这是《算法导论》上的例子,也是一个非常经典的问题。有n个需要在同一天使用同一个教室的活动a1,a2,…,an,教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后,活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠,ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。例如下图所示的活动集合S,其中各项活动按照结束时间单调递增排序。

考虑使用贪心算法的解法。为了方便,我们用不同颜色的线条代表每个活动,线条的长度就是活动所占据的时间段,蓝色的线条表示我们已经选择的活动;红色的线条表示我们没有选择的活动。
如果我们每次都选择开始时间最早的活动,不能得到最优解:

如果我们每次都选择持续时间最短的活动,不能得到最优解:

可以用数学归纳法证明,我们的贪心策略应该是每次选取结束时间最早的活动。直观上也很好理解,按这种方法选择相容活动为未安排活动留下尽可能多的时间。这也是把各项活动按照结束时间单调递增排序的原因。
(2)钱币找零问题
这个问题在我们的日常生活中就更加普遍了。假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元,至少要用多少张纸币?用贪心算法的思想,很显然,每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。在程序中已经事先将Value按照从小到大的顺序排好。
2、动态规划算法
当最优化问题具有重复子问题和最优子结构的时候,就是动态规划出场的时候了。动态规划算法的核心就是提供了一个memory来缓存重复子问题的结果,避免了递归的过程中的大量的重复计算。动态规划算法的难点在于怎么将问题转化为能够利用动态规划算法来解决。当重复子问题的数目比较小时,动态规划的效果也会很差。如果问题存在大量的重复子问题的话,那么动态规划对于效率的提高是非常恐怖的。
先看下面的例子:
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元?
我们凭直观感觉告诉自己,先选面值最大,因此最多选2枚5元的硬币,现在是10元了,还差一元,接下来我们挑选第二大的3元硬币,发现不行(10+3=13超了),因此我们继续选第三大的硬币也就是1元硬币,选一个就可以(10+1=11),所以总共用了3枚硬币凑够了11元。这就是贪心法,每次选最大的。但是我们将面值改为2元,3元和5元的硬币,再用贪心法就不行了。为什么呢?按照贪心思路,我们同样先取2枚最大5元硬币,现在10元了,还差一元,接下来选第二大的,发现不行,再选第三大的,还是不行,这时用贪心方法永远凑不出11元,但是你仔细看看,其实我们可以凑出11元的,2枚3元硬币和1枚五元硬币就行了,这是人经过思考判断出来了的,但是怎么让计算机算出来呢?这就要用动态规划的思想。
因此,可得贪心算法与动态规划算法的区别:
贪心算法:
1.贪心算法中,作出的每步贪心决策都无法改变,因为贪心策略是由上一步的最优解推导下一步的最优解,而上一部之前的最优解则不作保留。
2.由(1)中的介绍,可以知道贪心法正确的条件是:每一步的最优解一定包含上一步的最优解。
动态规划算法:
1.全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有最优解
2.动态规划的关键是状态转移方程,即如何由以求出的局部最优解来推导全局最优解
3.边界条件:即最简单的,可以直接得出的局部最优解
举例如下:
例1:台阶问题
有n级台阶,一个人每次上一级或者两级,问有多少种走完n级台阶的方法。
分析:动态规划的实现的关键在于能不能准确合理的用动态规划表来抽象出 实际问题。在这个问题上,我们让f(n)表示走上n级台阶的方法数。
那么当n为1时,f(n) = 1,n为2时,f(n) =2,就是说当台阶只有一级的时候,方法数是一种,台阶有两级的时候,方法数为2。那么当我们要走上n级台阶,必然是从n-1级台阶迈一步或者是从n-2级台阶迈两步,所以到达n级台阶的方法数必然是到达n-1级台阶的方法数加上到达n-2级台阶的方法数之和。即f(n) = f(n-1)+f(n-2),我们用dp
来表示动态规划表,dp[i],i>0,i<=n,表示到达i级台阶的方法数。
例2:0-1背包问题
01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >
e7a4
;= Wi ), f[i-1,j] }
f[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包中,可以取得的最大价值。Pi表示第i件物品的价值。
决策:为了背包中物品总价值最大化,第 i件物品应该放入背包中吗 ?
题目描述:
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
| name | weight | value | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a | 2 | 6 | 0 | 6 | 6 | 9 | 9 | 12 | 12 | 15 | 15 | 15 |
| b | 2 | 3 | 0 | 3 | 3 | 6 | 6 | 9 | 9 | 9 | 10 | 11 |
| c | 6 | 5 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 10 | 11 |
| d | 5 | 4 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 10 | 10 |
| e | 4 | 6 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
首先要明确这张表是至底向上,从左到右生成的。
为了叙述方便,用e2单元格表示e行2列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了。
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品e,d都不是这个背包能装的。
同理,c2=0,b2=3,a2=6。
总结,由上两例可以看出,动态规划算法的基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解
[b]3、分治算法
[/b]
分治算法的逻辑更简单了,就是一个词,分而治之。分治算法就是把一个大的问题分为若干个子问题,然后在子问题继续向下分,一直到base cases,通过base cases的解决,一步步向上,最终解决最初的大问题。
当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。这就是分治策略的基本思想。
[b]4、回溯算法[/b]
回溯算法是深度优先策略的典型应用,回溯算法就是沿着一条路向下走,如果此路不同了,则回溯到上一个
分岔路,在选一条路走,一直这样递归下去,直到遍历万所有的路径。八皇后问题是回溯算法的一个经典问题,还有一个经典的应用场景就是迷宫问题。
例1、八皇后问题
对于八皇后的求解可采用回溯算法,从上至下依次在每一行放置皇后,进行搜索,若在某一行的任意一列放置皇后均不能满足要求,则不再向下搜索,而进行回溯,回溯至有其他列可放置皇后的一行,再向下搜索,直到搜索至最后一行,找到可行解,输出。
可以使用递归函数实现上述回溯算法,递归函数用于求解在某一行放置皇后,具体代码如下所示。
代码
#include <stdlib.h>
#include <stdio.h>
int m[8][8] = {0};//表示棋盘,初始为0,表示未放置皇后
int num = 0;//解数目
//对于棋盘前row-1行已放置好皇后
//检查在第row行、第column列放置一枚皇后是否可行
bool check(int row,int column)
{
if(row==1) return true;
int i,j;
//纵向只能有一枚皇后
for(i=0;i<=row-2;i++)
{
if(m[i][column-1]==1) return false;
}
//左上至右下只能有一枚皇后
i = row-2;
j = i-(row-column);
while(i>=0&&j>=0)
{
if(m[i][j]==1) return false;
i--;
j--;
}
//右上至左下只能有一枚皇后
i = row-2;
j = row+column-i-2;
while(i>=0&&j<=7)
{
if(m[i][j]==1) return false;
i--;
j++;
}
return true;
}
//当已放置8枚皇后,为可行解时,输出棋盘
void output()
{
int i,j;
num++;
printf("answer %d:\n",num);
for(i=0;i<8;i++)
{
for(j=0;j<8;j++) printf("%d ",m[i][j]);
printf("\n");
}
}
//采用递归函数实现八皇后回溯算法
//该函数求解当棋盘前row-1行已放置好皇后,在第row行放置皇后
void solve(int row)
{
int j;
//考虑在第row行的各列放置皇后
for (j=0;j<8;j++)
{
//在其中一列放置皇后
m[row-1][j] = 1;
//检查在该列放置皇后是否可行
if (check(row,j+1)==true)
{
//若该列可放置皇后,且该列为最后一列,则找到一可行解,输出
if(row==8) output();
//若该列可放置皇后,则向下一行,继续搜索、求解
else solve(row+1);
}
//取出该列的皇后,进行回溯,在其他列放置皇后
m[row-1][j] = 0;
}
}
//主函数
int main()
{
//求解八皇后问题
solve(1);
return 0;
}
[b]5、分支限界算法[/b]
回溯算法是深度优先,那么分支限界法就是广度优先的一个经典的例子。回溯法一般来说是遍历整个解空间,获取问题的所有解,而分支限界法则是获取一个解(一般来说要获取最优解)。
例1、旅行商问题
省略
6、迭代法
迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法,即一次性解决问题。迭代法又分为精确迭代和近似迭代。“二分法”和“牛顿迭代法”属于近似迭代法。迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
举例1
一个饲养场引进一只刚出生的新品种兔子,这种兔子从出生的下一个月开始,每月新生一只兔子,新生的兔子也如此繁殖。如果所有的兔子都不死去,问到第 12 个月时,该饲养场共有兔子多少只?
分析:这是一个典型的递推问题。我们不妨假设第 1 个月时兔子的只数为 u 1 ,第 2 个月时兔子的只数为 u 2 ,第 3 个月时兔子的只数为 u 3 ,……根据题意,“这种兔子从出生的下一个月开始,每月新生一只兔子”,则有
u 1 = 1 , u 2 = u 1 + u 1 × 1 = 2 , u 3 = u 2 + u 2 × 1 = 4 ,……
根据这个规律,可以归纳出下面的递推公式:
u n = u(n - 1)× 2 (n ≥ 2)。这样就可递推出第12个月时兔子的总数量。
相关文章推荐
- 一种 Deformable Parts Model (DPM) 快速检测算法的简介与进一步加速
- 自编码器及相关变种算法简介
- 多模式串匹配之AC自动机算法(Aho-Corasick算法)简介与C语言程序实现源码参考
- Java☞DES加解密算法简介及实现
- MD5的简介以及实现其算法原理的各种语言的代码
- [转载]深度学习(Deep Learning)综述及算法简介[转]
- Hubble.Net 0.1 版本算法简介
- 推荐算法之简介
- 球面数据拟合算法简介
- 【算法】Trie数(前缀树/字典树)简介及Leetcode上关于前缀树的题
- 贪心算法总结及实例简介
- 数据结构和算法学习01-数据结构和算法简介
- 2、算法简介(笔记)
- Gradient Boosting算法简介
- 算法设计方法------分治法(分而治之)简介
- 算法简介—模拟退火算法
- 【转】最短路径算法-三种算法简介
- 算法及其分析简介
- 麻省理工公开课《算法导论》笔记([第1集] 课程简介及算法分析)
- 数据结构之算法简介
