动态规划之0-1背包问题，钢条切割

动态规划

首先说说动态规划：动态规划与分治法相似，都是组合子问题的解来解决原问题的解，与分治法的不同在于：分治法的子问题是相互独立存在的，而动态规划应用于子问题重叠的情况。

设计动态规划算法的步骤：

1、刻画一个最优解的结构特征

2、递归地定义最优解的值

3、计算最优解的值，通常采用自底向上的方法

4、利用算出的信息构造一个最优解

0-1背包问题

例题：假设现有容量10kg的背包，另外有3个物品，分别为a1，a2，a3。物品a1重量为3kg，价值为4；物品a2重量为4kg，价值为5；物品a3重量为5kg，价值为6。将哪些物品放入背包可使得背包中的总价值最大？

public static void main(String[] args) {

int w[] = {3, 4, 5};
int p[] = {4, 5, 6};
int m = 10;
int n = 3;
int c[][] = beibao(m,n,w,p);
for (int i = 0; i <=n; i++) {
for (int j = 0; j <=m; j++) {
System.out.print(c[i][j]+"\t");
if(j==m){
System.out.println();
}
}
}
}
/**
*
* @param m 背包的最大承重量
* @param n 物品的个数
* @param w 物品的重量集合
* @param p 物品的价值集合
* @return 二维数组 代表 对应的商品数量和背包重量 的最大价值
*  说明：
*  w[i] :  第i+1个物体的重量；
*  p[i] : 第i+1个物体的价值；
*  c[i][m] ： 前i个物体放入容量为m的背包的最大价值；
*  c[i-1][m] ： 前i-1个物体放入容量为m的背包的最大价值；
*  c[i-1][m-w[i]] ： 前i-1个物体放入容量为m-w[i]的背包的最大价值；
*  取最优解公式：
*  c[i][m]=max{c[i-1][m-w[i]]+pi , c[i-1][m]} 根据前面的最优解 取得当前的最优解
*/
public static int[][] beibao(int m,int n,int[] w,int[] p){
// 定义最优解集合:  n=3 m=10  而二维数组c的下标为 i =[0-3] j=[0-10]
int[][] c = new int[n+1][m+1];
//初始化 二维数组c 第1列的值为0  代表 当 背包的最大重量为0时 前 i个物品的最大价值
for(int i=0;i<n+1;i++){
c[i][0] = 0;
}
//初始化 二维数组c 第一行的值为0  代表 当 前0个物品  背包最大重量为j 的最大价值
for(int j=0;j<m+1;j++){
c[0][j] = 0;
}
// 循环前 1-3个物品
for(int i=1;i<n+1;i++){
//循环 前i个物品下的背包最大重量 1-10
for(int j=1;j<m+1;j++){
//step1:当 背包的最大重量 大于等于 第i个物品的重量 时 说明能放下第i个物品
if (w[i - 1] <= j) {
//step2:判断前c[i - 1][j]的最优解 是否小于 c[i - 1][j - w[i - 1]] + p[i - 1]的值
if (c[i - 1][j] < (c[i - 1][j - w[i - 1]] + p[i - 1])) {
c[i][j] = c[i - 1][j - w[i - 1]] + p[i - 1];
}else {
c[i][j] = c[i - 1][j];
}
} else {
c[i][j] = c[i - 1][j];
}
}
}
return c;
}

结果图：

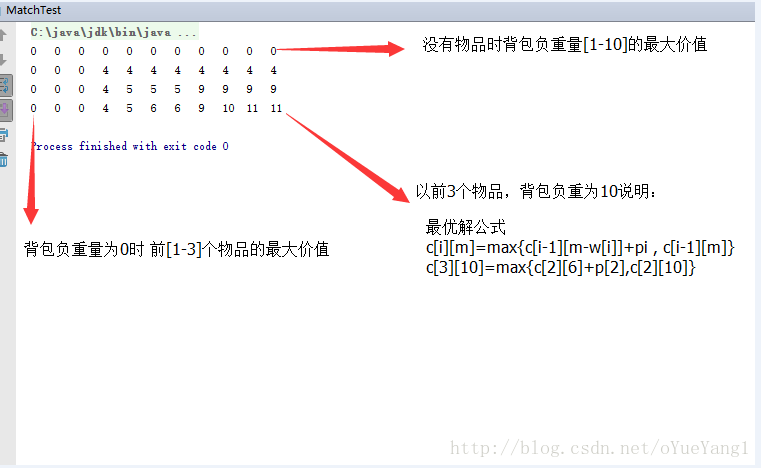
钢条切割问题

例题：给定一段长度为n英寸的钢条和一个价格表 pi (i=1,2, …,n)，求切割钢条的方案，使得销售收益rn最大。注意，如果长度为n英寸的钢条价格pn足够大，最优解可能就是完全不需要切割。

若钢条的长度为i，则钢条的价格为Pi，如何对给定长度的钢条进行切割能得到最大收益？

长度i 1 2 3 4 5 6 7 8 9 10

价格Pi 1 5 8 9 10 17 17 20 14 30

public static void main(String[] args) {
int []p = {-1,1, 5, 8, 9, 10, 17, 17, 20, 14, 30};
System.out.println(toDownToUp(p,7));
}

/**
*
* @param p 锯条价格列表
* @param n 锯条长度
* @return r数组 长度为[0-n]的最优解
*/
public static int toDownToUp(int[] p ,int n){
int[] r = new int[n+1];
for (int i = 0; i < r.length; i++) {
r[i] = 0;
}
return downToUp(p,n,r);
}

/**
* 自底向上刻画最优解
* @param p 锯条价格列表
* @param n 锯条长度
* @param r 最优解列表
* @return
*
* 说明：
* 从1-n 逐一刻画Rn的最优解
* 刻画最优解是依赖于已经刻画过的最优解进行分析
*/
public static int downToUp(int[] p ,int n,int[] r){
//循环长度[1-n] 刻画最[1-n]的最优解
for(int i=1;i<=n;i++){
//初始化定义 i 长度的最优解
int q = -9999;
//循环 i 长度的所有 分割方案
for(int j=1;j<=i;j++){
//取i长度的所有方案中的最优解
q = max(q,p[j]+r[i-j]);
}
//赋值到最优解集合中。
r[i] = q;
}
return r
;
}

public static int max(int a,int b){
return a>b?a:b;
}