5. 机器学习基石-Why can Machine Learn?

Why can Machine Learn?

Why can Machine Learn?

1. Preview of Last Chapter

2. VC Bound (Vapnik-Chervonenkis Bound) - A Upper Bound Limitation of Hoeffding Inequity

1) Introduction

2) Growth function

3) Different Types of Growth function

① Growth Function for Positive Rays

② Growth Function for Positive Interval

③ Growth Function for Convex Sets

4) Break Point of Growth function

5) Bounding Function

① Introduction of Bounding Function

② Proof of Bounding Function

6) Vapnik-Chervonenkis (VC) bound

3. The VC Dimension

1) Definition of VC Dimension

2) Generalization Error

3) Model Complexity

4) How much Data We need Theoretically and Practically

Summary

Reference

这一节我的思路是把老师的第五，六、七节的内容结合起来了，并且思路不完全按照老师的授课来走。

1. Preview of Last Chapter

因为这一章的讨论是基于上一章最后一节得到的公式的，所以我们先Recap一下。

上一节中，我们最后得出公式（1）（2）

ρ[BADD]≤2M⋅exp(−2ϵ2N)(1)

ρ[∣Ein(g)−Eout(g)∣>ϵ]≤2M⋅exp(−2ϵ2N)(2)

这里的M是一个有限的数，所以当训练样本 N 越大，那么Bad Data出现的概率越低，Ein≈Eout；如果训练样本 N一定的情况下，M越大，也就是说Hypothesis越多，那样可以供我们用算法 A进行选择的越多，那么越有可能选到一个好的样本，使得 Ein≈0

总结如下表：

-	M很小的时候	M很大的时候	N很小的时候	N很大的时候
Ein(g)≈Eout(g)	Yes，Bad Data的数量也少了	No，Bad Data的数量也多了	Yes，Bad Data出现的概率变小了	No，Bad Data出现的概率变大了
Ein(g)≈0	No，选到低错误率的可能性变小了	Yes，选到低错误率的可能性变大了	没必然联系，样本总数多于少，与错误率无关	没必然联系，样本总数多于少，与错误率无关

从表格中可以看出，M 太大太小都会对机器学习的有效性造成影响，所以我们要进一步缩小M 的取值范围。

问题：怎么缩小M的取值范围

解决方案：在上一节中，我们再推导的过程中使用了联合上限（Union Bound)，造成实际的上限被放大了很多。因为在做集合的或运算的时候，我们单纯的把各个集合加起来，但是却没有减去他们的交集部分，所以造成了上限被放大的问题。

关于Union Bound 的推导可以看这个链接Boole’s inequality

总的来说就是因为我们推导公式（1）的时候使用了Union Bound，所以导致了不等式右边的值（上限）被放大了，所以现在我们可以把它进行缩减，求出有效的 M值(即 MH(N))，下面我们来推导这个有效值。

2. VC Bound (Vapnik-Chervonenkis Bound) - A Upper Bound Limitation of Hoeffding Inequity

1) Introduction

场景：对于不同数量N的训练数据，有多少种不同的方法 effective(N) 可以区分他们？

当 N=1 的时候，如图一所示，共有2种方法，effective(N)=2=21。



图一 N=1 [1]

当 N=2 的时候，如图二所示，共有4种方法，effective(N)=4=22。



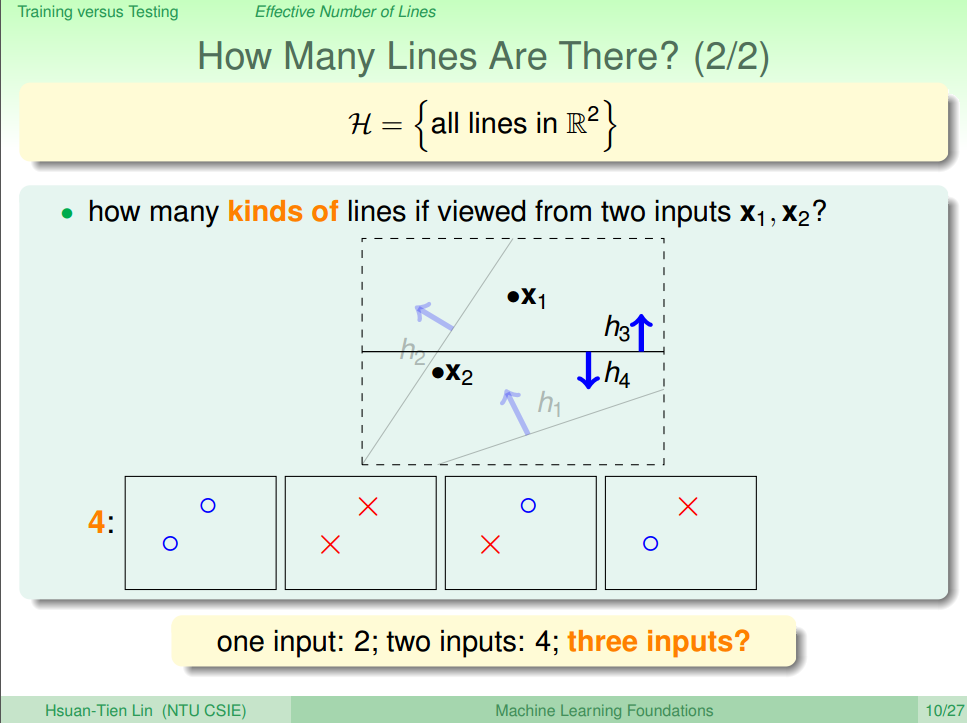
图二 N=2 [1]

当 N=3 的时候，如图三、四所示，最多有8种方法，虽然说在特定的情形下，可能只有6中种方法，effective(N)=8=23。



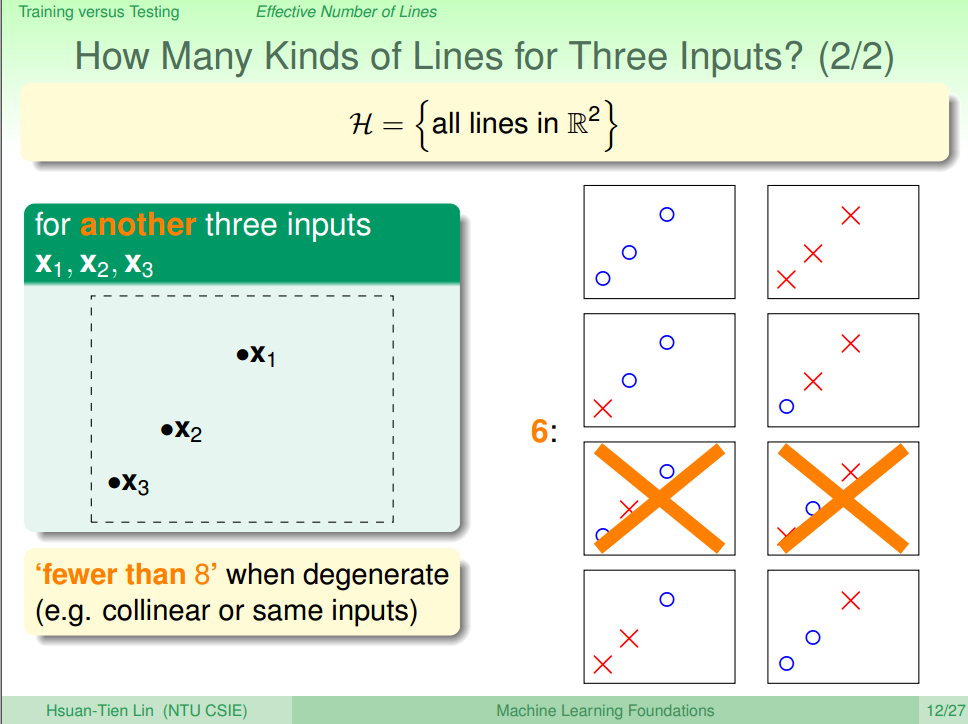
图三 N=3 with error [2]



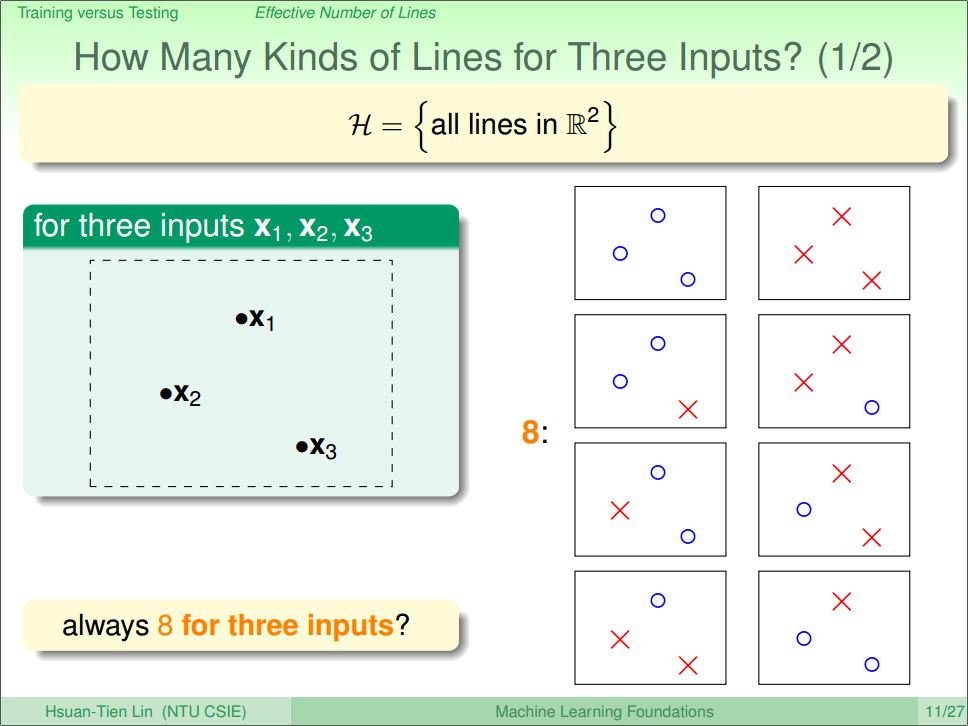
图四 N=3 [1]

当 N=4 的时候，如图五所示，无论怎么放着4个点，最多只有14种方法，effective(N)=14<24。



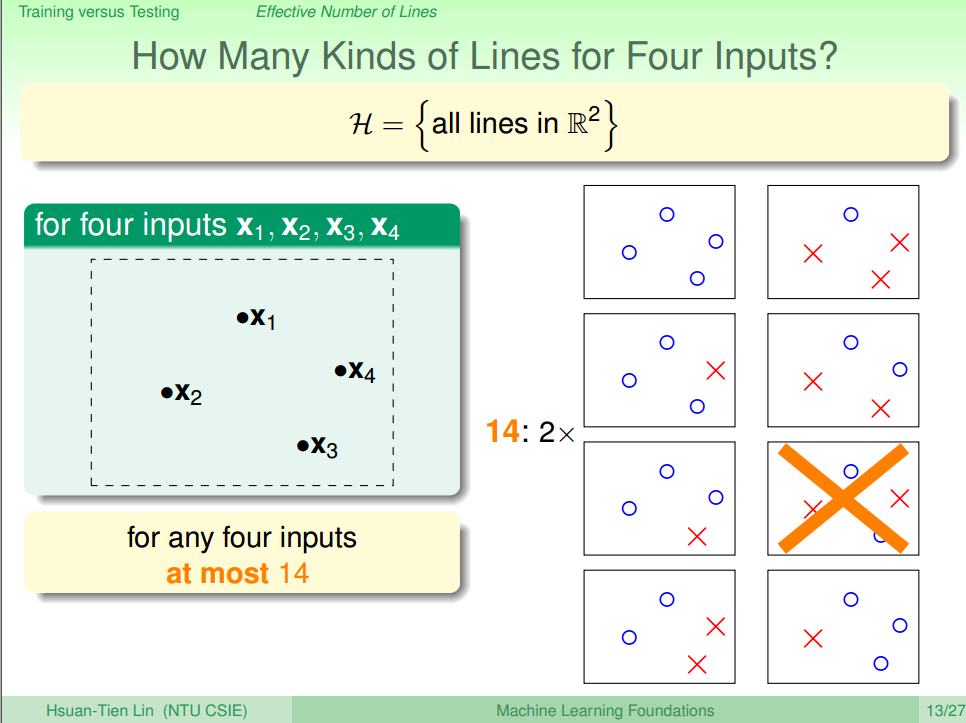
图五 N=4 [1]

当 N=5 的时候，很显然 effective(N)=32<25，就不再继续讨论了。

总结如下表：

N	effctive(N)
1	2=21
2	4=22
3	8=23
4	14<25
5	32<<26
…	…
N	effctive(N)<<2N

总结如图六，可以看出当 N>4的时候，effective(N)<2N，也就是说我们把 M和N 的关系构建了起来，所以我们可以用 effective(N) 去替换 M，得到公式(3)

ρ[∣Ein(g)−Eout(g)∣>ϵ]≤2⋅effective(N)⋅exp(−2ϵ2N)(3)



图六 Summary [1]

2) Growth function

上面Binary Clasification的分类方法叫做二分类法（dichotomy)，为了更好地表示 N和effective(N) 的关系，我们引入成长函数（Growth Function) MH(N) 来表示，具体的数学表达如公式（4）所示。

MH(N)=maxx1,x2,...,xN∈X∣H(x1,x2,...,xN)∣(其中，上限为2N)(4)

3) Different Types of Growth function

① Growth Function for Positive Rays

Positive Rays 是用一个一维向量作用于一维坐标上，与该向量同方向的值为+1，反方向为-1

如图七所示，Postives Rays 的成长函数为 MH(N)=(N−1)，当 N≥2的时候，MH(N)<2N=O(N)



图七 Growth Function for Positive Rays [2]

② Growth Function for Positive Interval

Positive Interval 是用一个一维“线段”作用于一维坐标上，与在线段里面的值为+1，外面的为-1

如图八所示，Positive Interval 的成长函数为 MH(N)=C2N+1+1=12N2+12N+1，当 N≥3的时候，MH(N)<2N=O(N2)



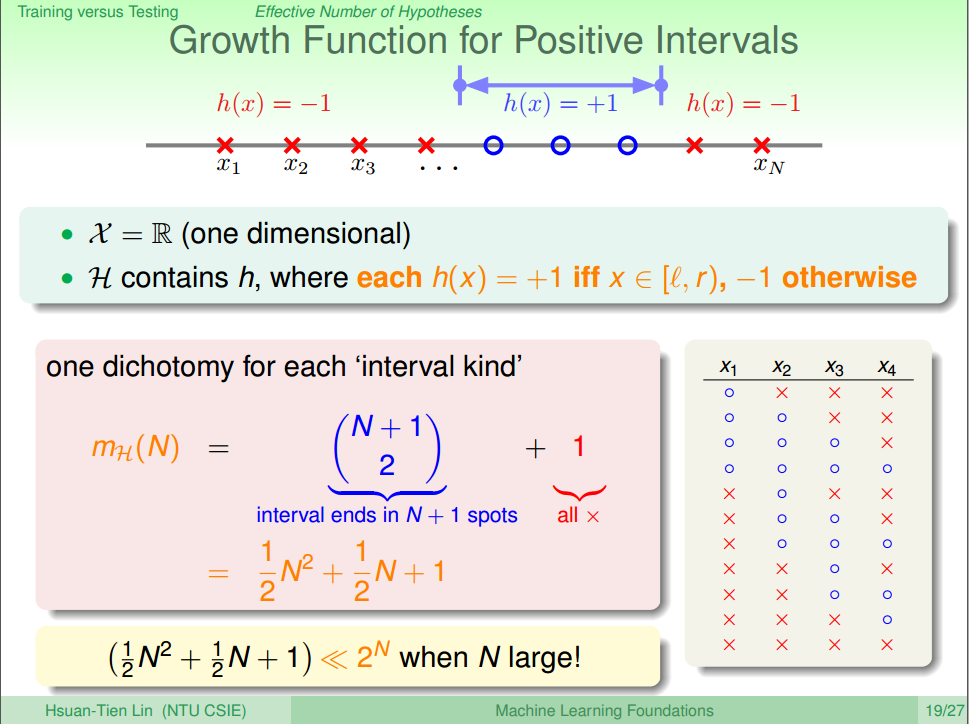
图八 Growth Function for Positive Interval [2]

③ Growth Function for Convex Sets

Convex Sets 不太好理解。可以理解成在二维坐标上，用凸多边形去把所需要的点串起来。在多边形顶点上的点的值为+1，不在的为-1。因为我们讨论的是最大的可能性，所以当我们把所有的点都放在一个圆上的时候，必定存在一个凸多边形可以连接任意多个点（即可以画出任意多边形），然后再把所有点的组合情况加起来

如图九所示，Convex Setsl 的成长函数为 MH(N)=∑i=0NCNi=2N



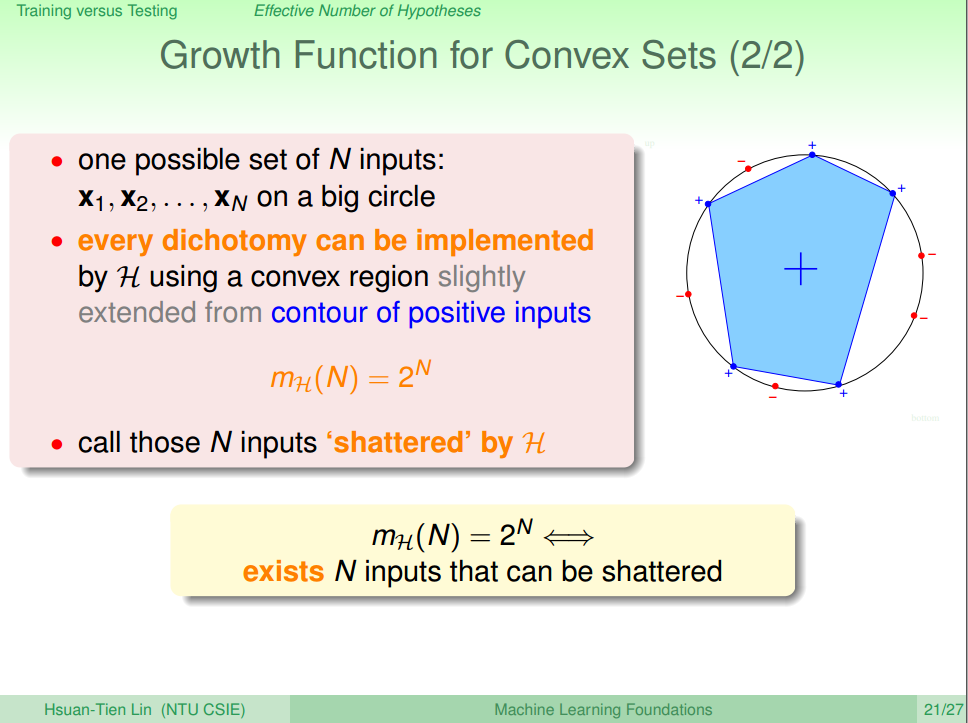
图九 Growth Function for Convex Sets [2]

4) Break Point of Growth function

我们称能满足完全二分类(出现不同种类的数量为2N)的情况为shattered,能shattered的最大的点为突破点(break point)。

然后根据上面对N从1-5的尝试，得到的最大可能性如下表

N	effctive(N)
1	2=21
2	4=22
3	8=23
4	14<25
5	32<<26
…	…
N	effctive(N)<<2N

可以推断出公式（3）

effctive(N):MH(N)≤max(possibleMH(N)Givenbreak−point(K))≤2N(3)

上面关于Growth Function讨论的几种情况的Break Point 如图十所示，我们可以看出成长函数的复杂度与Break Point的大小存在一定的关系。



图十 Break Point of Growth function [3]

5) Bounding Function

① Introduction of Bounding Function

根据上一节的Break Point K和样本点 N的关系，我们引入一个新概念，上限函数(Bounding Function) B(N,K)。这个函数表示有N个样本点且成长函数的突破点是K的时候，最多有多少种组合情况，比如说B(3,2)=3（这个比较容易想象，这里就不展开讨论了）。并且这个上限函数满足公式（4），因为这是采用而分类的方法来进行的，最大值为2N。

B(N,K)≤2N(3)

但是显然在上面的例子中，我们可以看到B(N,K)<2N(N≥K)，所以我们下面进一步确定这个上限函数的最大值。

② Proof of Bounding Function

我们下面用表格的方式来表示B(N,K) 表格如下表，我们下面将会填满这个表格来找出相应的规律

B(N,K)	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1							…
N=2							…
N=3							…
N=4							…
N=5							…
N=6							…
…							…

1.根据上面的规律，我们知道在N<K的时候，B(N,K)=2N，所以表格更新如下

B(N,K)	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1		2	2	2	2	2	…
N=2			4	4	4	4	…
N=3				8	8	8	…
N=4					16	16	…
N=5						32	…
N=6							…
…							…

2. 然后当K=1的时候，我们至少有一种分法（全正或者全负），所以第一列全部为1，表格更新如下。

B(N,K)	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1	1	2	2	2	2	2	…
N=2	1		4	4	4	4	…
N=3	1			8	8	8	…
N=4	1				16	16	…
N=5	1					32	…
N=6	1						…
…	1						…

3. 接着，当N=K的时候，我们上面也可以看到，所有的值最大都等于2N−1(因为不能所有情况都出现一次)，所以表格更新如下。

B(N,K)	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1	1	2	2	2	2	2	…
N=2	1	3	4	4	4	4	…
N=3	1		7	8	8	8	…
N=4	1			15	16	16	…
N=5	1				31	32	…
N=6	1					63	…
…	1						…

4. 在之前的章节，我们也数过B(3,2)=4，其实看到这里我们已经大概有一些规律了：下面一项为上面两项之和， B(N,K)=B(N−1,K)+B(N−1,K−1)。当然我们只是猜测，下面我们继续证明。表格更新如下：

B(N,K)	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1	1	2	2	2	2	2	…
N=2	1	3	4	4	4	4	…
N=3	1	4	7	8	8	8	…
N=4	1			15	16	16	…
N=5	1				31	32	…
N=6	1					63	…
…	1						…

5.我们证明上面的猜想B(N,K)=B(N−1,K)+B(N−1,K−1)

1）首先我们遍历B(4,3)，可以得到图十一的结果，然后我们整理了一下结果的顺序，可以发现橙色区域 {x1,x2,x3}结果分别出现了2次，而紫色区域的{x1,x2,x3}结果只出现了1次。



图十一 Reorganized Dichotomies of B(4,3) - 1 [4]

2）所以我们单独把{x1,x2,x3}，提出来看，并把橙色区域的个数设为 α，紫色区域的个数为 β，那么原来4个点的情况 B(4,3)=2α+β，而3个点的情况 B(3,3)=α+β，如下图十二所示。



图十一 Reorganized Dichotomies of B(4,3) - 2 [4]

3)接着我们单独看 α可以发现这个刚好是 B(3,2) 的最大可能性，也就是说 α≤B(3,2)=4，如图十三所示。



图十一 Reorganized Dichotomies of B(4,3) - 3 [4]

4） 根据上面的分析，我们目前得到三个公式，如下面的公式（4）（5）（6）。

B(4,5)=2⋅α+β(4)

α+β≤B(3,3)(5)

α≤B(3,2)(6)

所以把公式(5)(6)加起来，我们可以更新公式（4）为公式（7）

B(4,5)≤2⋅α+β(7)

5）最后我们用同样的方法来研究B(N,K)可以很容易证明到公式（8）（9）（10）

B(N−1,K)≤∑i=0k−1CiN−1(8)

B(N−1,K−1)≤∑i=0k−2CiN−1=∑i=1k−1CiN−1(9)

B(N,K)≤B(N−1,K)+B(N−1,K−1)≤∑i=0k−1CiN−1+∑i=1k−1CiN−1=C0N−1+∑i=1k−1(CiN−1+CiN−1)=1+∑i=1k−1CiN=C0N+∑i=1k−1CiN=∑i=0k−1CiN(10)

所以我们的表格更新如下：

B(N,K)	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1	1	2	2	2	2	2	…
N=2	1	3	4	4	4	4	…
N=3	1	4	7	8	8	8	…
N=4	1	≤5	11	15	16	16	…
N=5	1	≤6	≤16	≤15	31	32	…
N=6	1	≤7	≤22	≤26	≤57	63	…
…	1	…	…	…	…	…	…

我们再把NK−1的表格整理如下：

NN−1	K=1	K=2	K=3	K=4	K=5	K=6	…
N=1	1	1	1	1	1	1	…
N=2	1	2	4	8	8	16	…
N=3	1	3	9	27	27	81	…
N=4	1	4	16	64	64	256	…
N=5	1	5	25	125	125	625	…
N=6	1	6	36	216	216	1296	…
…	…	…	…	…	…	…	…

对比图参考老师上课的PPT，如图十二所示。



图十二 Comparision of B(N,K) and N^(K-1) [6]

总结起来就是：在N≥2,K≥3的时候，总有公式（11）的情况。

MH(N)≤B(N,K)=∑i=0K−1≤NK−1(11)

6) Vapnik-Chervonenkis (VC) bound

@TODO: 这一节主要是证明从数学的角度上证明VC Bound 并以此更新Hoeffding Inequity。目前听得失一知半解，所以只贴出结论，后面再补充。

结论如图十三所示。



图十三 Vapnik-Chervonenkis (VC) bound [5]

这个VC Bound的作用是把之前Hoeffding的参数 M替换成这里引入的成长函数 MH(N)，并构建出成长函数与样本数量（N）的关系这样的话，我们就可以容易的得到结论：在样本N足够大时候，发生Bad Data的概率小于 epsilon (Ein≈Eout)，可以得出错误率也低(Ein≈0)，说明机器学习是可能的。

也就是说要说机器可以学习必须满足下面的条件：

1. 假设空间的成长函数 MH(N) 存在Break Point K （即有一个好的假设空间H)

2. 输入数据的样本 N 足够大（有一个好的数据集 D）

3. 存在一个算法，能够找出能在假设空间 H 中找到一个值使得错误率 Ein 足够小 （有一个好的算法 A –>也就是我们后面会研究的重点）

其中：条件1和2通过VC Bound保证了 Ein≈Eout，条件3保证了 Ein≈0 ⟹ Machine Can Learn.

3. The VC Dimension

1) Definition of VC Dimension

VC Dimension( dvc )指的是能够使得成长函数可以被shatter的最大值（即 Break Point - 1)，用符号表示为公式（12）。

dvc=min(K)−1(12)

上面的Hoeffding Inequity可以变成公式（13）

ρ[∣Ein(g)−Eout(g)∣>ϵ]≤4⋅(2N)dvc⋅exp(−18ϵ2N)(13)

因此，根据这个特点，我们只要确保一个成长函数存在 VC Dimension，我们就可以确定他存在Break Point，是一个好的假设空间。

2) Generalization Error

我们引入泛化误差 δ 表示 Ein(g)和Eout(g) 的接近程度，即 δ=Ein(g)−Eout(g) ，根据公式（13），我们稍作化简，如公式（14）。

δ4(2N)dvcδϵ=4⋅(2N)dvc⋅exp(−18ϵ2N)=exp(18ϵ2N)=8N⋅ln(4(2N)dvcδ)−−−−−−−−−−−−−−√(14)

也就是说 Ein(g)−Eout(g) 的误差会小于等于 8N⋅ln(4(2N)dvcδ)−−−−−−−−−−−−√。 所以我们可以求得 Eout 的范围如公式（15）

Ein(g)−8N⋅ln(4(2N)dvcδ)−−−−−−−−−−−−−−√≤Eout(g)≤Ein(g)+8N⋅ln(4(2N)dvcδ)−−−−−−−−−−−−−−√)(15)

3) Model Complexity

上一节，我们求出了 Ein(g)−Eout(g) 的误差，为了方便引用，我们引入了新的概念：模型复杂度（Model Complexitiy）来表示这个误差值，数学表示如公式（16）

Ω(N,H,δ)=8N⋅ln(4(2N)dvcδ)−−−−−−−−−−−−−−√(15)

可以看出，随着VC Dimension的增大，Ω也会变大，然后 Ein(g) 也会随着VC Dimension的增大而变小（因为选择的假设空间大了），但是 Eout(g) 却不是一个单调函数，因为公式（15），然后这2个值一个变大一个变小，但是最终的话，Eout 的曲线是先下降，然后上升: 遍历一边就可以得到结果了，所以找到 d∗vc 很重要。(因为 Eout 才是我们机器学习最重要的指标）

结果如图十四所示。



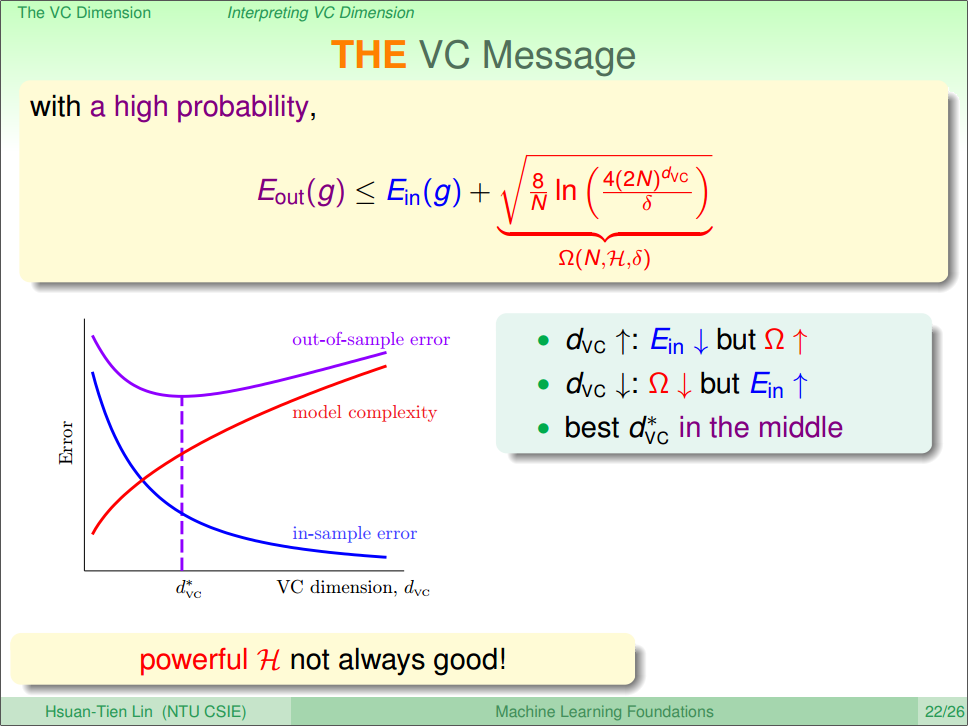
图十四 Error and VC dimension [6]

4) How much Data We need Theoretically and Practically

问题：假如现在老板给员工下达了一个任务，要求这个模型的 ϵ=0.1，δ=0.1，dvc=3 ，那样的话，我们需要多少个样本 N 才能满足要求呢？

回答：根据上面的公式（14），分别代入参数到等式中，可以求得样本数量 N 如图十五的橙色区域所示。但是实际上，我们只需要 10dvc就足够了。



图十五 How much Data We need Theoretically and Practically [6]

因为我们在计算的时候同样的把上限给放大了，放大的原因如下所示:

1. Hoeffding Inequity 不需要知道未知的情况，但是VC Bound可以用于各种分布，各种目标函数(因为 VC Bound的推导是基于不同的N和K)；

2. 在给Binary Classification 强行装上成长函数本身就是一个宽松的上界，但是VC Bound可以用于各种数据样本；

3. 使用二项式 Ndvc 作为成长函数的上界使得约束更加宽松，但是VC Bound可以用于任意具有相同VC维的假设空间；

4. 联合限制（union bound）并不是一定会选择出现不好事情的假设函数，但是VC Bound可以用于任意算法。

Summary

我们首先通过回顾上一节的内容，得到结论是根据Hoeffding Inquity: 要使得机器可以学习的条件是 ① Ein≈Eout ② Ein≈0

接着我们讨论了什么情况下才能保证这2个条件满足，进行了讨论，最终我们通过引入① Growth Function ② Break Point ③ VC Bound, VC Dimension 更改Hoeffding Inequity的上限，最终得到我们需要的答案：

假设空间的成长函数 MH(N) 存在Break Point K （即有一个好的假设空间 H)

输入数据的样本 N 足够大（有一个好的数据集 D）

存在一个算法，能够找出能在假设空间 H 中找到一个值使得错误率 Ein 足够小 （有一个好的算法 A –>也就是我们后面会研究的重点）

其中：条件1和2通过VC Bound保证了 Ein≈Eout，条件3保证了 Ein≈0 ⟹ Machine Can Learn.

之后我们讨论了理论上 N≈10000dvc 而实际上只需要 N≈10dvc 的能使得 Eout 最小，并且分析了为什么理论上和实际上差别这么大

Reference

[1]机器学习基石(台湾大学-林轩田)\5\5 - 2 - Effective Number of Lines (15-26)

[2]机器学习基石(台湾大学-林轩田)\5\5 - 3 - Effective Number of Hypotheses (16-17)

[3]机器学习基石(台湾大学-林轩田)\5\5 - 4 - Break Point (07-44)

[4]机器学习基石(台湾大学-林轩田)\6\6 - 3 - Bounding Function- Inductive Cases (14-47)

[5]机器学习基石(台湾大学-林轩田)\6\6 - 4 - A Pictorial Proof (16-01)

[6]机器学习基石(台湾大学-林轩田)\7\7 - 4 - Interpreting VC Dimension (17-13)