大数据算法课程笔记2：2D Convex Hull

1. 题目简介

Input: n points in the plane p1,p2,⋯,pn, where pi=(xi,yi)

Output: 包含所有点的最小凸多边形的所有边

2. 基本思想 ：Divide and Conquer

先把点集一分为二，分别求取相应凸多边形，然后对两个凸多边形合并。

3. 具体算法

sort P={pi} for i=1⋯n, such that x1<x2<⋯xn

divide P into PL and PR equally by picking the median of X, xmedian. Then PL={pi} iff. xi<xmedian, and PR=P−PL

After division, do it recursively.

Merge: that’s the difficult part and we will expand it in detail.

4. 融合两个凸多边形

这部分是对具体算法第四部分的展开。

输入是两个点集以及包含相应点集的最小凸多边形，且有两个点集的X域不交叉，求一个O(N)的融合算法。

讨论包含所有点的最小凸多边形的性质。笔者能够想到的最简单的方法就是枚举任意三个点，然后对所有三个点所构成的三角形取并集。

但这个算法明显是O(N！)的。如果能够找到一个比较好的切入点，就会大幅降低了算法复杂度。

如下图所示，黑色菱形为已经计算好的两个凸多边形。对两者进行融合，其实是去寻找合理的两条红边，只需要讨论红边应该具有什么性质即可。



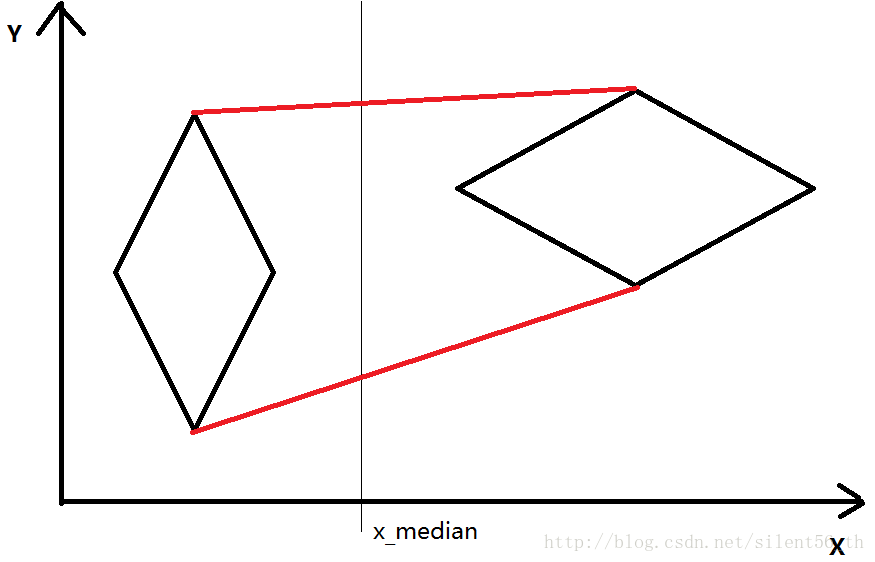
这个性质很直接了，凸多边形应该包含点集里面的所有点，并且因为是凸多边形，即所有角度数小于180°。

综上所述，对于上面的红边，应该有点集里面的所有点都比红边低，否则比红边高的点将不会被包含在以红边为边的所有凸多边形内。

形式化上诉结论有：

minxmedian∗a+bs.t. xi∗a+b≥yi, for all i

这是一个只有两个变量的线性规划问题，后面会解释，求解此问题复杂性为O(N)。

得到红边之后，逐一比较xi∗a+b和yi，若两者相等，则该点为凸多边形的顶点。

5. 整体算法的时间复杂度

如上所诉，有T(N)=T(N/2)+O(N)，容易求解T(N)=O(NlogN)。

6. 算法复杂性与数据性质的关系

若N极大，则复杂性为O(1)。

证明：因为推广N到inf，则覆盖全域，凸多边形为包含全域的凸多边形。

若已知最终的凸多边形的边数一定，为h。则复杂性最终为O(Nlogh)。

证明：将求解凸多边形问题转换为求解凸多边形所有边的问题，进而可以将其转换为求解凸多边形上边和下边的问题。

易证凸多边形的顶点中必然存在(x1,y1)和(xN,yN)，其中x1=min(x),xN=max(x)。 然后对凸多边形的边根据pmin和pmax进行划分，分为上边集和下边集，上边集和下边集交集为NULL，并集为所有边，上边位于所有下边上方。如下图所示，红边为上边，黑边为下边。



​ 上边和下边的数目最多为h，现计算求解上边集的算法复杂性。

​ T(N,h)=T(N/2,h1)+T(N/2,h2)+O(N)，其中h=h1+h2+1。

​ 假设T(N,h)=O(Nlogh)，使用归纳法即可验证。

T(N,h)=CN2log(h1)+CN2log(h2)+O(N) =CN2log(h1h2)+O(N) ≤CN2log(h24)+O(N) ≤CN(logh−1)+O(N) ≤CNlogh iff. C is big enough