算法基础-->贪心和动态规划
2017-09-05 23:23
399 查看
本篇博文将详细总结贪心和动态规划部分,贪心和动态规划是非常难以理解和掌握的,但是在笔试面试中经常遇到,关键还是要理解和掌握其思想,然后就是多刷刷相关一些算法题就不难了。本篇将会大篇幅总结其算法思想。

相应的,对于 Ai+1 ,需考察前 i 个状态集A1,A2…Ai−1,Ai 才可完成整个推理过程,往往称之为高阶马尔科夫模型:

高阶马尔科夫模型的推理,叫做“动态规划”,而马尔科夫模型的推理,对应“贪心法”。
计算A[i] 时不需要A[i+1…n−1] 的值——未来
这一处理过程一直持续到 n 个输入都被考虑完毕,则记入最优解集合中的输入子集构成这种量度意义下的问题的最优解。 这种能够得到某种量度意义下的最优解的分级处理方法称为贪心方法。
单个字符构成的字符串,显然是回文串;所以,这个的划分一定是存在的。
如:s=“aab”,返回
“aa”,“b”;
“a”,“a”,“b”。
剪枝:在每一步都可以判断中间结果是否为合法结果。
回溯+剪枝——如果某一次发现划分不合法,立刻对该分支限界。
一个长度为 n 的字符串,最多有 n−1 个位置可以截断,每个位置有两种选择,因此时间复杂度为O(2n−1)=O(2n) 。
在利用 DFS 解决这个问题时,我们还需要解决一个小问题,如何判断一个子串 str[i,i+1,...,j],0<=i<n,i<=j<n 是否回文?
线性探索:j 从 i 到 n−1 遍历即可,从字符串 str[i,i+1,...,j] 两端开始比较,然后得出是否对称回文。
事先缓存所有 str[i,i+1,..,j] 是回文串的那些记录,用二维布尔数组 p[n][n] 的 true/false 表示 str[i,i+1,...,j] 是否是回文串。
它本身是个小的动态规划:如果已知 str[i+1,...,j−1] 是回文串,那么判断 str[i,i+1,...,j] 是否是回文串,只需要判断 str[i]==str[j] 就可以了。
算法:
将集合 φ(i+1) 置空;
遍历 j(0≤j<i),若 str[j,j+1…i] 是回文串,则将 str[j…i] 添加到 φ(j−1),然后再把 φ(j−1) 添加到 φ(i+1) 中;
i 从0 到n,依次调用上面两步,最终返回 φ(n) 即为所求。
DFS 的过程,是计算完成了 str[0…i] 的切分,然后递归调用,继续计算 str[i+1,i+2…n−1] 的过程;
而 DP 中,假定得到了 str[0…i−1] 的所有可能切分方案,如何扩展得到 str[0…i] 的切分;
上述两种方法都可以从后向前计算得到对偶的分析。
从本质上说,二者是等价的:最终都搜索了一颗隐式树。
DFS 显然是深度优先搜索的过程,而 DP 更像层序遍历 的过程。
如果只计算回文划分的最少数目,动态规划更有优势;如果计算所有回文划分,DFS 的空间复杂度比DP 略优。
实例:
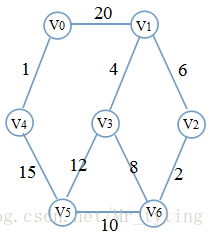
Prim 过程,假定从 V0 开始:
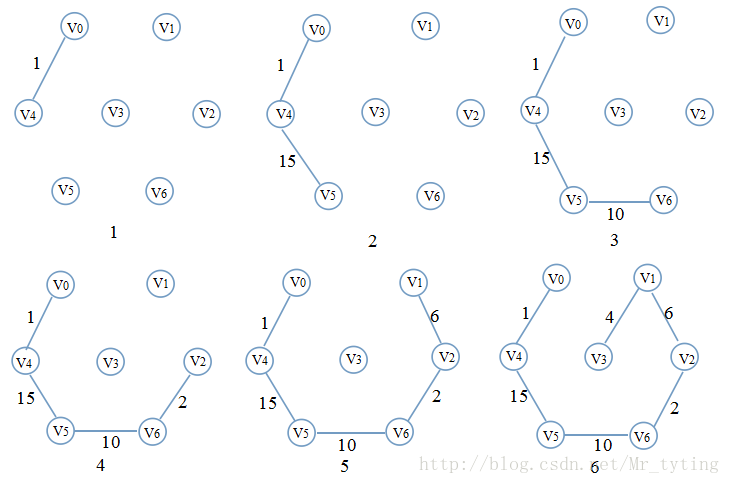
实现代码:
实例:
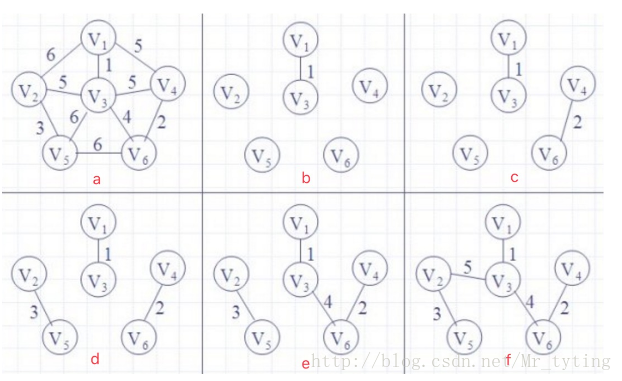
在实现kruskal 时,我们需要了解一下并查集,请看该链接 并查集详解
基于 kruskal算法的特点,我们存储一个图的方式将不会使用邻接表或者邻接矩阵,而是直接存储边,具体的数据结构如下所示,重载小于操作符的目的是为了方便对边进行排序。
实现代码:
S 为已经找到的从v0 出发的最短路径的终点集合,它的初始状态为空集,那么从v0 出发到图中其余各顶点(终点)vi(vi∈V−S) ,记arcs[i][j] 为结点 vi 直接到达 结点 vj 的距离。记d[j] 为源点 v0 到达结点 vj 的最短距离。初始时:d[j]=arcs[0][j]
选择 vj,使得 d[j]=minj(d[i],vi∈V−S),vj 就是当前求得的一条从 v0 出发的最短路径的终点。令 S=S∪j;
修改从 v0 出发到集合 V−S 上任一顶点vk 可达的最短路径长度。如果 d[j]+arcs[j][k]<d[k], 则修改 d[k] 为:d[k]=d[j]+arcs[j][k];
以上2,3 步骤重复 n−1 次。
在网上找了个Dijkstra 图例过程:
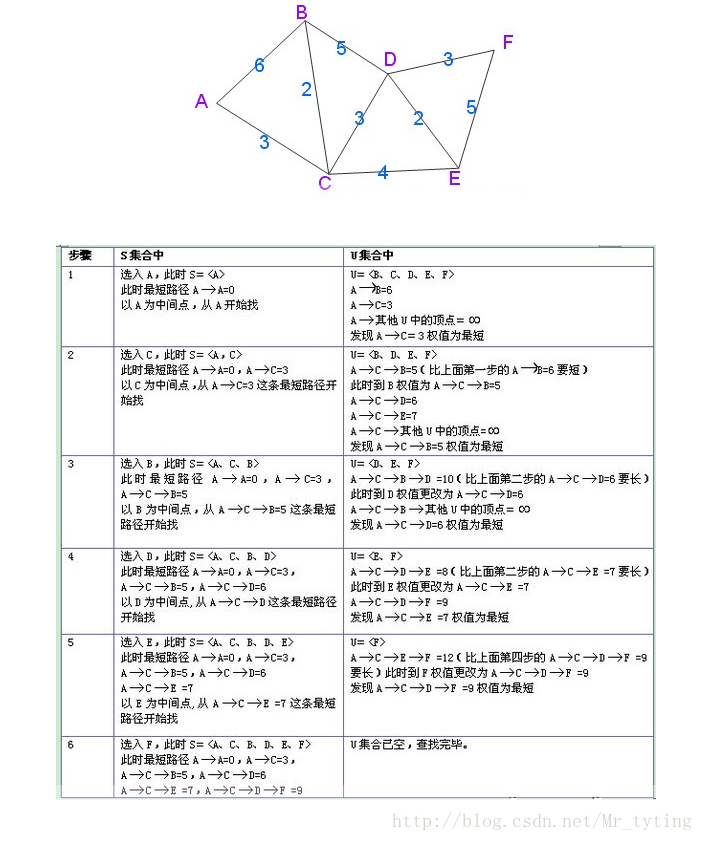
实现代码:
以上几种算法的状态转移示意图如下,是一个马尔科夫过程:

可以看到,在从Ai 到Ai+1 的扩展过程中,上述三个算法都没有使用 A[0…i−1] 的值。
以序列 1,4,6,2,8,9,7 为例。
显然以 9 结尾的递增序列 1,4,6,8,9 长度最长为 5。
记 A 的前i 个字符构成的前缀串 为Ai=a0,a1,a2...ai−1 ,以ai 结尾的最长递增子序列记做 Li ,其长度记为b[i];
假定已经计算得到了b[0,1…,i−1],如何计算b[i] 呢 ?
已知L0,L1……Li−1 的前提下,如何求Li ?
从而:b[i]={max(b[j])+1,0≤j<i且aj≤ai}
计算b[i]:遍历在i 之前的所有位置j,找出满足条件aj≤ai 的最大的 b[j]+1;
计算得到 b[0…n−1] 后,遍历所有的b[i],找出最大值即为最大递增子序列的长度。
时间复杂度为O(N2)。
三个矩阵A、B、C的阶分别是a0×a1,a1×a2,a2×a3 ,从而(A×B)×C和A×(B×C) 的乘法次数是a0a1a2+a0a2a3、a1a2a3+a0a1a3 ,二者一般情况是不相等的。那么如何使得计算量最小呢?
给定n 个矩阵A1,A2,…,An,其中Ai与Ai+1 是可乘的,i=1,2…,n−1。考察该n 个矩阵的连乘积:A1×A2×A3……×An ,确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的乘法次数最少。
将矩阵连乘积记为A[i:j] ,这里i≤j,显然,若i==j,则A[i:j] 即A[i] 本身。
考察计算A[i:j] 的最优计算次序。设这个计算次序在矩阵Ak 和Ak+1之间将矩阵链断开,i≤k<j,则其相应的完全加括号方式为:(Ai,Ai+1...Ak)(Ak+1,Ak+2,...,Aj)
计算量:A[i:k] 的计算量加上A[k+1:j] 的计算量,再加上A[i:k] 和A[k+1:j] 相乘的计算量。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
最优子结构性质是可以使用动态规划算法求解的显著特征。
记 Ai 的维度为 pi−1∗pi
当i==j 时,A[i:j] 即Ai 本身,因此,m[i,i]=0;(i=1,2,…,n)
当i<j 时有:
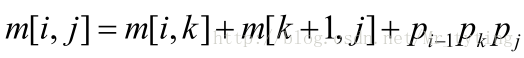
k 遍历(i,j),找到一个使得计算量最小的k,也即是:
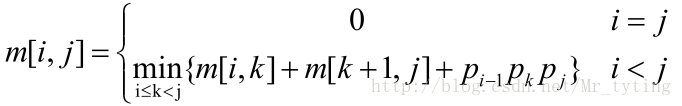
i 不断从1 扩展到 n,j 从i 扩展,随着问题规模越来越大,总能求出 m[1,n]。
如果面额都是1 元的,则无论总额多少,可行的组合数显然都为1。
如果面额多一种,则组合数有什么变化呢?
定义dp[i][j]:使用面额小于等于 i 的钱币,凑成j 元钱,共有多少种组合方法。
dp[100][500]=dp[50][500]+dp[100][400]
dp[50][500]:50 以下的面额的组成500 是一种组合方式,这里面就包括了dp[20][500],dp[10][500]等
dp[100][400]:表示首先拿出100 的面额,剩余的 400 用小于等于100 的面额组合。
上述两种组合方式没有包含关系,两种组合合在一起组成所有的组合方式。
dp[i][j]=dp[ismall][j]+dp[i][j−i]
如果把 i 看成数组下标,则有:dp[i][j]=dp[i−1][j]+dp[i][j−dom[i]]
从而有:
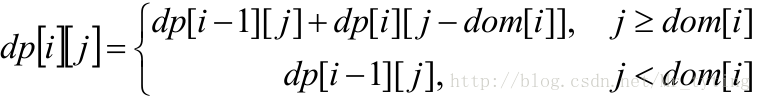
初始条件( 注意都为1,而不是0):
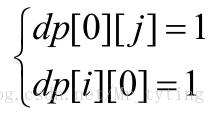
按照上面的状态转移方差我们可以从初始状态一直推导到终止状态dp[6][100w]
原状态转移方程:
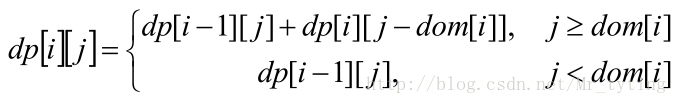
滚动数组版本的状态转移方程:

这个 last[j] 就是原始状态转移方程中的dp[i−1][j] 。dp[j] 就是dp[i][j]。
在动态规划的问题中,如果不求具体解的内容,而只是求解的数目,往往可以使用滚动数组的方式降低空间使用量(甚至空间复杂度),由于滚动数组减少了维度,甚至代码会更简单,但是代码会更加难以理解。
若当前位于(x,y) 处,它来自于哪些格子呢?
dp[x,y] 表示从起点走到坐标为(x,y) 的方格的最小权值。
dp[0,0]=a[0,0], 第一行(列)累积
dp[x,y]=min(dp[x−1,y]+a[x,y],dp[x,y−1]+a[x,y])
即:dp[x,y]=min(dp[x−1,y],dp[x,y−1])+a[x,y]
状态转移方程:
⎧⎩⎨⎪⎪dp(i,0)=∑ik=0chess[k][0]dp(0,j)=∑jk=0chess[0][k]dp(i,j)=min(dp(i−1,j),dp(i,j−1))+chess[i][j]
在上边界时只能向右走,在左边界时只能向下走。
滚动数组去除第一维:{dp(j)=∑ik=0chess[0][k]dp(0,j)=min(dp(j),dp(j−1))+chess[i][j]
只能从左边或者上边进入一个格子。
如果 (i,j) 被占用,dp[i][j]=0
如果(i,j) 不被占用,dp[i][j]=dp[i−1][j]+dp[i][j–1]
故状态转移方程:⎧⎩⎨dp[i][0]=dp[0][j]=1dp[i][j]=0dp[i][j]=dp[i−1][j]+dp[i][j−1](i=0||j=0)(i,j)被占用(i,j)没被占用
一共要走m+n–2 步,其中(m–1) 步向右,(n−1) 步向下。组合数C(m+n–2,m−1)=C(m+n−2,n−1)

我们把 A 点看着起点 (0,0) ,计算起点A 到终点 B 的所有路径allPath,然后再计算 A 到 p 的所有路径path1 ,再计算p 到B 的所有路径paht2 ,那么paht1∗path2 即是从起点 A 到终点B 的所有经过点 p 的路径数,allPath−paht1∗paht2 即为避开点p 从A 到点B 的所有路径。

动态规划是方法论,是解决一大类问题的通用思路。事实上,很多内容都可以归结为动态规划的思想。
何时可以考虑使用动态规划:
初始规模下能够方便的得出结论
空串、长度为0的数组、自身等’
能够得到问题规模增大导致的变化
递推式——状态转移方程
在实践中往往忽略无后效性
哪些题目不适合用动态规划?
状态转移方程 的推导,往往陷入局部而忽略全局。在重视动态规划的同时,别忘了从总体把握问题。
贪心和动态规划思想
马尔科夫模型
对于 Ai+1 ,只需考察前一个状态 Ai, 即可完成整个推理过程,它的特点是状态 Ai 只由 Ai−1 确定,与状态 A1…Ai−2 无关,在图论中,常常称之为 马尔科夫模型:
相应的,对于 Ai+1 ,需考察前 i 个状态集A1,A2…Ai−1,Ai 才可完成整个推理过程,往往称之为高阶马尔科夫模型:

高阶马尔科夫模型的推理,叫做“动态规划”,而马尔科夫模型的推理,对应“贪心法”。
无后效性
计算A[i] 时只读取A[0…i−1],不修改——历史计算A[i] 时不需要A[i+1…n−1] 的值——未来
理解贪心,动态规划:
动态规划:
可以如下理解动态规划:计算 A[i+1] 只需要知道 A[0…i] 的值,无需知道 A[0…i] 是通过何种途径计算得到的——只需知道它们当前的状态值本身即可。如果将 A[0…i] 的全体作为一个整体,则可以认为动态规划法是马尔科夫过程,而非高阶马尔科夫过程。贪心:
根据实际问题,选取一种度量标准。然后按照这种标准对 n 个输入排序,并按序一次输入一个量。如果输入和当前已构成在这种量度意义下的部分最优解加在一起不能产生一个可行解,则不把此输入加到这部分解中。否则,将当前输入合并到部分解中从而得到包含当前输入的新的部分解。这一处理过程一直持续到 n 个输入都被考虑完毕,则记入最优解集合中的输入子集构成这种量度意义下的问题的最优解。 这种能够得到某种量度意义下的最优解的分级处理方法称为贪心方法。
字符串回文划分问题
问题描述
给定一个字符串 str,将 str 划分成若干子串,使得每一个子串都是回文串。计算 str 的所有可能的划分。单个字符构成的字符串,显然是回文串;所以,这个的划分一定是存在的。
如:s=“aab”,返回
“aa”,“b”;
“a”,“a”,“b”。
方法一:深度优先搜索
思考:若当前计算得到了 str[0…i−1] 的所有划分,可否添加 str[i…j],得到更大的划分呢?显然,若str[i…j] 是回文串,则可以添加。剪枝:在每一步都可以判断中间结果是否为合法结果。
回溯+剪枝——如果某一次发现划分不合法,立刻对该分支限界。
一个长度为 n 的字符串,最多有 n−1 个位置可以截断,每个位置有两种选择,因此时间复杂度为O(2n−1)=O(2n) 。
在利用 DFS 解决这个问题时,我们还需要解决一个小问题,如何判断一个子串 str[i,i+1,...,j],0<=i<n,i<=j<n 是否回文?
线性探索:j 从 i 到 n−1 遍历即可,从字符串 str[i,i+1,...,j] 两端开始比较,然后得出是否对称回文。
事先缓存所有 str[i,i+1,..,j] 是回文串的那些记录,用二维布尔数组 p[n][n] 的 true/false 表示 str[i,i+1,...,j] 是否是回文串。
它本身是个小的动态规划:如果已知 str[i+1,...,j−1] 是回文串,那么判断 str[i,i+1,...,j] 是否是回文串,只需要判断 str[i]==str[j] 就可以了。
// 判断str[i,j]回文与否
void CalcSubstringPalindrome(const char* str, int size, vector<vector<bool>>& p)
{
int i, j;
for (i = 0; i < size; i++)
p[i][i] = true;//单个字符肯定是回文串
for (i = size - 2; i >= 0; i--)
{
p[i][i + 1] == (str[i] == str[i + 1]);//得出字符串内每两个相邻字符回文与否,也就是得出初始状态
for (j = i + 2; j < size; j++)//以i子串左端并且在内循环i固定,j为子串右端,并且j不断向外扩展,
//递进的判断str[i,j]回文与否
{
if ((str[i] == str[j]) && p[i + 1][j - 1])
p[i][j] = true;
}
}
}
//以str[nStart]为起点,不断的判断str[nSart,i]回文与否,若是回文加入solution
void FindSolution(const char* str, int size, int nStart, vector<vector<string>>& all, vector<string>& solution, const vector<vector<bool>>& p)
{
if (nStart >= size)//表示当前方向递归深入到头
{
all.push_back(solution);//将当前方向的所有回文压入到all
return;
}
for (int i = nStart; i < size; i++)
{
if (p[nStart][i])
{
solution.push_back(string(str + nStart, str + i + 1));
FindSolution(str, size, i + 1, all, solution, p);//沿着这个方向深入递归
solution.pop_back();//回溯到当前初始状态,选择其他方向
}
}
}
void MinPalindrome3(const char* str, vector<vector<string>>& all)
{
int size = (int)strlen(str);
vector<vector<bool>> p(size, vector<bool>(size));
CalcSubstringPalindrome(str, size, p);
vector<string> solution;
FindSolution(str, size, 0, all, solution, p);
}方法二:动态规划
如果已知:str[0…i−1] 的所有回文划分 φ(i),(这个 i 表示回文长度, 显然每个回文是个 vector ,长度为 i 的回文有多个,故 φ 是个vector<vector<string>> 类型的,可以理解为二维数组)如何求 str[0…i] 的所有划分呢? 如果子串 str[j…i] 是回文串,则将该子串和 φ(j−1) 共同添加到 φ(i+1) 中(长度为 j−1 的每个回文都添加上该回文子串)。算法:
将集合 φ(i+1) 置空;
遍历 j(0≤j<i),若 str[j,j+1…i] 是回文串,则将 str[j…i] 添加到 φ(j−1),然后再把 φ(j−1) 添加到 φ(i+1) 中;
i 从0 到n,依次调用上面两步,最终返回 φ(n) 即为所求。
//to 表示prefix[i],长度为i的回文集合;from表示prefix[j]长度为j的回文集合;sub表示要添加的回文str[j,i]
void Add(vector<vector<string>>& to, const vector<vector<string>>& from, const string& sub)
{
if (from.empty())//from 为空时,直接将sub压入to
{
to.push_back(vector<string>(1, sub));//vector<string>(1, sub):初始化vector,长度为1,一个字符串sub
return;
}
to.reserve(from.size());
for (vector<vector<string>>::const_iterator it = from.begin(); it != from.end(); it++)//遍历from里面每个回文
{
to.push_back(vector<string>());
vector<string>& now = to.back();
now.reserve(it->size() + 1);
//将from某个个回文里面的每个字符依次压入now,然后在末尾加上要添加的回文子串sub
for (vector<string>::const_iterator s = it->begin(); s != it->end(); s++)
now.push_back(*s);
now.push_back(sub);
}
}
void MinPalindrome4(const char* str, vector<vector<string>>& all)
{
int size = (int)strlen(str);
vector<vector<bool>> p(size, vector<bool>(size));
CalcSubstringPalindrome(str, size, p);
vector<vector<string>>* prefix = new vector<vector<string>>[size];//注意这里是vector<vector>* 相当于一个三维数组
prefix[0].clear();
int i, j;
for (i = 1; i <= size; i++)
{
for (j = 0; j < i; j++)
{
if (p[j][i - 1])//prefix[i]表示长度为i的回文集合,这里是指长度,那么索引应该到i-1
{
Add((i == size) ? all : prefix[i], prefix[j], string(str + j, str + i));
}
}
}
delete[] prefix;
}DFS和DP的深刻认识
显然DFS 比DP 好理解,而代码上DP 更加简洁。DFS 的过程,是计算完成了 str[0…i] 的切分,然后递归调用,继续计算 str[i+1,i+2…n−1] 的过程;
而 DP 中,假定得到了 str[0…i−1] 的所有可能切分方案,如何扩展得到 str[0…i] 的切分;
上述两种方法都可以从后向前计算得到对偶的分析。
从本质上说,二者是等价的:最终都搜索了一颗隐式树。
DFS 显然是深度优先搜索的过程,而 DP 更像层序遍历 的过程。
如果只计算回文划分的最少数目,动态规划更有优势;如果计算所有回文划分,DFS 的空间复杂度比DP 略优。
利用贪心思想的几个重要算法
最小生成树MST
最小生成树要求从一个带权无向连通图中选择 n-1 条边并使这个图仍然连通(也即得到了一棵生成树),同时还要考虑使树的权最小。为了得到最小生成树,人们设计了很多算法,最著名的有 Prim 算法和Kruskal 算法,这两个算法都是贪心算法。Prim算法
Prim 算法是解决最小生成树的常用算法。它采取贪心策略,从指定的顶点开始寻找最小权值的邻接点。图 G=<V,E> ,初始时 S=V0,把与 V0 相邻接,且边的权值最小的顶点加入到 S。不断地把 S 中的顶点与 V−S 中顶点的最小权值边加入(不可能形成环),直到所有顶点都已加入到 S 中。实例:

Prim 过程,假定从 V0 开始:

实现代码:
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#define MAXINT 6
using namespace std;
//声明一个二维数组,C[i][j]存储的是点i到点j的边的权值,如果不可达,则用1000表示
//借此二维数组来表示一个连通带权图
int c[MAXINT][MAXINT] = { { 1000, 6, 1, 5, 1000, 1000 }, { 6, 1000, 5, 1000, 3, 1000 }, { 1, 5, 1000, 5, 6, 4 }, { 5, 1000, 5, 1000, 1000, 2 }, { 1000, 3, 6, 1000, 1000, 6 }, { 1000, 1000, 4, 2, 6, 1000 } };
void Prim(int n)
{
int lowcost[MAXINT];//lowcost[i]表示V-S中的点i到达S的最小权值
int closest[MAXINT];//closest[i]表示V-S中的点i到达S的最小权值S中对应的点
bool s[MAXINT];//bool型变量的S数组表示i是否已经包括在S中
int i, k;
s[0] = true;//从第一个结点开始寻找,扩展
for (i = 1; i <= n; i++)//简单初始化,这个时候S为{0},V-S为{1,2,3,4,5}
{
lowcost[i] = c[0][i];//这个时候S中只有0
closest[i] = 0;//现在所有的点对应的已经在S中的最近的点是1
s[i] = false;
}
cout << "0->";
for (i = 0; i<n; i++)//执行n次,也即是向S中添加所有的n个结点
{
int min = 1000;//最小值,设大一点的值,后面用来记录lowcost数组中的最小值
int j = 1;
for (k = 1; k <= n; k++)//寻找lowcost中的最小值,并且找出此时V-S中对应的点j
{
if ((lowcost[k]<min) && (!s[k]))
{
min = lowcost[k]; j = k;
}
}
cout << j << " " << "->";
s[j] = true;//添加点j到集合S中
for (k = 1; k <= n; k++)//因为新加入了j点,需要更新V-S到S的最小权值,只需要与刚加进来的c[j][k]比较即可
{
if ((c[j][k]<lowcost[k]) && (!s[k])){ lowcost[k] = c[j][k]; closest[k] = j; }
}
}
}
int main()
{
Prim(MAXINT - 1);
return 0;
}Kruskal算法
Kruskal 算法:将边按照权值递增排序,每次选择权值最小并且不构成环的边,重复 n−1 次。实例:

在实现kruskal 时,我们需要了解一下并查集,请看该链接 并查集详解
基于 kruskal算法的特点,我们存储一个图的方式将不会使用邻接表或者邻接矩阵,而是直接存储边,具体的数据结构如下所示,重载小于操作符的目的是为了方便对边进行排序。
实现代码:
#include <iostream>
#include <vector>
#include <algorithm>
#include <fstream>
using namespace std;
struct Edge
{
int u; //边连接的一个顶点编号
int v; //边连接另一个顶点编号
int w; //边的权值
friend bool operator<(const Edge& E1, const Edge& E2)
{
return E1.w < E2.w;
}
};
//创建并查集,uset[i]存放结点i的根结点,初始时结点i的根结点即为自身
void MakeSet(vector<int>& uset, int n)
{
uset.assign(n, 0);
for (int i = 0; i < n; i++)
uset[i] = i;
}
//查找当前元素所在集合的代表元
int FindSet(vector<int>& uset, int u)
{
int i = u;
while (uset[i] != i) i = uset[i];
return i;
}
void Kruskal(const vector<Edge>& edges, int n)
{
vector<int> uset;
vector<Edge> SpanTree;
int Cost = 0, e1, e2;
MakeSet(uset, n);
for (int i = 0; i < edges.size(); i++) //按权值从小到大的顺序取边
{
e1 = FindSet(uset, edges[i].u);
e2 = FindSet(uset, edges[i].v);
if (e1 != e2) //若当前边连接的两个结点在不同集合中,选取该边并合并这两个集合,如果相等连接则成环
{
SpanTree.push_back(edges[i]);
Cost += edges[i].w;
uset[e1] = e2; //合并当前边连接的两个顶点所在集合
}
}
cout << "Result:\n";
cout << "Cost: " << Cost << endl;
cout << "Edges:\n";
for (int j = 0; j < SpanTree.size(); j++)
cout << SpanTree[j].u << " " << SpanTree[j].v << " " << SpanTree[j].w << endl;
cout << endl;
}
int main()
{
int n, m;
cin >> n >> m;
vector<Edge> edges;
edges.assign(m, Edge());
for (int i = 0; i < m; i++)
cin >> edges[i].u >> edges[i].v >> edges[i].w;
sort(edges.begin(), edges.end()); //排序之后,可以以边权值从小到大的顺序选取边
Kruskal(edges, n);
system("pause");
return 0;
}Dijkstra最短路径算法
该算法为单源点最短路径算法,要求边的权值为正数。在图 G(V,E) 中,假定源点为 v0,结点集合记 V ,将结点集合分为两部分,分别为集合 S,集合 V−S :S 为已经找到的从v0 出发的最短路径的终点集合,它的初始状态为空集,那么从v0 出发到图中其余各顶点(终点)vi(vi∈V−S) ,记arcs[i][j] 为结点 vi 直接到达 结点 vj 的距离。记d[j] 为源点 v0 到达结点 vj 的最短距离。初始时:d[j]=arcs[0][j]
选择 vj,使得 d[j]=minj(d[i],vi∈V−S),vj 就是当前求得的一条从 v0 出发的最短路径的终点。令 S=S∪j;
修改从 v0 出发到集合 V−S 上任一顶点vk 可达的最短路径长度。如果 d[j]+arcs[j][k]<d[k], 则修改 d[k] 为:d[k]=d[j]+arcs[j][k];
以上2,3 步骤重复 n−1 次。
在网上找了个Dijkstra 图例过程:

实现代码:
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#include<set>
#include<queue>
using namespace std;
const int MAXINT = 32767;
const int MAXNUM = 10;//结点总数
int d[MAXNUM];//单源点到其他结点的最短路径
int prev[MAXNUM];//记录前驱结点
int arcs[MAXNUM][MAXNUM];//邻接矩阵,arcs[i][j]也即是两结点(vi,vj)之间的直接距离
void Dijkstra(int v0, int* prev)//源点 v0
{
bool S[MAXNUM];// 判断是否已存入该点到S集合中
int n = MAXNUM;
for (int i = 1; i <= n; ++i)
{
d[i] = arcs[v0][i];//初始时最短距离为直接距离
S[i] = false;// 初始都未用过该点
if (d[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
}
d[v0] = 0;
S[v0] = true;//S集合中加入v0
for (int i = 2; i <= n; i++)
{
int mindist = MAXINT;
int u = v0; // 找出当前未使用的点j的dist[j]最小值
for (int j = 1; j <= n; ++j)
if ((!S[j]) && d[j] < mindist)
{
u = j; // u为在V-S中到源点v0的最短距离对应的结点
mindist = d[j];
}
S[u] = true;//将u加入到S中
//更新其他结点到单源点的最短距离,查看其他结点经过u到单源点的距离会不会比之前单元点的直接距离要短
for (int j = 1; j <= n; j++)
if ((!S[j]) && arcs[u][j]<MAXINT)
{
if (d[u] + arcs[u][j] < d[j])//在通过新加入的u点路径找到离v0点更短的路径
{
d[j] = d[u] + arcs[u][j]; //更新dist
prev[j] = u; //记录前驱顶点
}
}
}
}总结
Prim算法与贪心
Prim 算法中,计算 V−S 中每个结点 到 S 的最小权值,也就是最小距离,然后把距离最小的那个结点加入到 S 中,并且在 V−S 中剔除该结点。那么计算 V−S 中每个结点的最短距离成为问题的关键所在。显然只有在加入新的最短结点到 S 中时,V−S 中每个结点的最短距离才会可能发生改变,我们定义把距离最短的那个结点加入到 S时中称为状态,那么该状态结果只取决于上一个状态。这是一种典型的贪心思想。Kruskal算法与贪心
对边的权值进行从小到大的排序,依次加入小的权值边,且不能形成环,我们把边的集合 E 分成两部分,一部分S,另一部分U ,S 表示已经加入的边集合,U 表示候选的边集合,我们需要对U 集合里面的边权值进行从小到大的排序,U 中的每个边都要其对应的排名,每次向S 中加入U 中排名最高的边也就是取决于其排名,我们定义每次加入一条边为一个状态,那么当前的状态只是取决于上一次的状态,上一次向S 中加入了哪条边,则在U 中剔除该边,则剩余的边排名就发生改变,需要更新。Dijkstra算法与贪心
只需要对Prim 算法稍作变化就能得到 Dijkstra 算法,故与贪心的联系参考上面的 Prim 。以上几种算法的状态转移示意图如下,是一个马尔科夫过程:

可以看到,在从Ai 到Ai+1 的扩展过程中,上述三个算法都没有使用 A[0…i−1] 的值。
最长递增子序列LIS
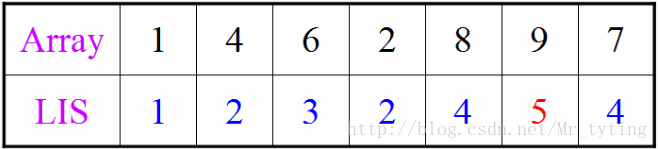
在字符串部分我们详解过这个问题,利用的是最长公共子序列解的,现在我们尝试利用动态规划解。以序列 1,4,6,2,8,9,7 为例。
前缀分析
以 1 结尾的递增序列[1] ,长度为 1;以 4 结尾的递增序列 [1,4],长度为 2;以 6 结尾的递增序列 [1,4,6] ,长度为3;同理可得下面表格:
显然以 9 结尾的递增序列 1,4,6,8,9 长度最长为 5。
LIS记号
长度为 N 的数组记为 A=[a0,a1,a2...an−1]记 A 的前i 个字符构成的前缀串 为Ai=a0,a1,a2...ai−1 ,以ai 结尾的最长递增子序列记做 Li ,其长度记为b[i];
假定已经计算得到了b[0,1…,i−1],如何计算b[i] 呢 ?
已知L0,L1……Li−1 的前提下,如何求Li ?
求解LIS
根据定义, Li 必须以ai 结尾; 如果将ai 分别缀到L0,L1……Li−1 后面,是否允许呢?如果 ai≥aj ,则可以将ai 缀到Lj 的后面,得到比Lj 更长的字符串。从而:b[i]={max(b[j])+1,0≤j<i且aj≤ai}
计算b[i]:遍历在i 之前的所有位置j,找出满足条件aj≤ai 的最大的 b[j]+1;
计算得到 b[0…n−1] 后,遍历所有的b[i],找出最大值即为最大递增子序列的长度。
时间复杂度为O(N2)。
实现代码
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
using namespace std;
int LIS(const int *p, int length, int *pre, int& nIndex)
{
int* longest = new int[length];//longest[i]表示以p[i]结尾的递增序列长度
int i, j;
for (i = 0; i < length; i++)
{
longest[i] = 1;//初始时以每个字符结尾的递增序列长度都为1
pre[i] = -1;
}
int nLst = 1;//最长的递增子序列长度
nIndex = 0;
for (i = 1; i < length; i++)
{
for (j = 0; j < i; j++)
{
if (p[j] <= p[i])
{
if (longest[i] < longest[j] + 1)
{
longest[i] = longest[j] + 1;
pre[i] = j;//记录前驱
}
}
}
if (nLst < longest[i])//记录所有的递增子序列里面最长的长度
{
nLst = longest[i];
nIndex = i;//nIndex记录最长递增子序列最后一个结点
}
}
delete[] longest;
return nLst;
}
void GetLIS(const int* array, const int* pre, int nIndex, vector<int>& lis)
{
while (nIndex>=0)//nIndex为最长递增子序列最后一个结点
{
lis.push_back(array[nIndex]);
nIndex = pre[nIndex];
}
reverse(lis.begin(), lis.end());//逆向输出
}
void Print(int *p, int size)
{
for (int i = 0; i < size; i++)
cout << p[i]<<" ";
cout << endl;
}
int main()
{
int array[] = { 1, 4, 5, 6, 2, 3, 8, 9, 10, 11, 12, 12, 1 };
int size = sizeof(array) / sizeof(int);
int* pre = new int[size];
int nIndex;
int max = LIS(array, size, pre, nIndex);
vector<int> lis;
GetLIS(array, pre, nIndex, lis);
delete[] pre;
cout << max << endl;
Print(&lis.front(), (int)lis.size());
return 0;
}矩阵乘积
问题描述
根据矩阵相乘的定义来计算C=A×B,需要m∗n∗s 次乘法。三个矩阵A、B、C的阶分别是a0×a1,a1×a2,a2×a3 ,从而(A×B)×C和A×(B×C) 的乘法次数是a0a1a2+a0a2a3、a1a2a3+a0a1a3 ,二者一般情况是不相等的。那么如何使得计算量最小呢?
问题分析
可以利用矩阵乘法的结合律 来降低乘法的计算量。给定n 个矩阵A1,A2,…,An,其中Ai与Ai+1 是可乘的,i=1,2…,n−1。考察该n 个矩阵的连乘积:A1×A2×A3……×An ,确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的乘法次数最少。
将矩阵连乘积记为A[i:j] ,这里i≤j,显然,若i==j,则A[i:j] 即A[i] 本身。
考察计算A[i:j] 的最优计算次序。设这个计算次序在矩阵Ak 和Ak+1之间将矩阵链断开,i≤k<j,则其相应的完全加括号方式为:(Ai,Ai+1...Ak)(Ak+1,Ak+2,...,Aj)
计算量:A[i:k] 的计算量加上A[k+1:j] 的计算量,再加上A[i:k] 和A[k+1:j] 相乘的计算量。
最优子结构
特征:计算A[i:j] 的最优次序所包含的计算矩阵子链 A[i:k] 和A[k+1:j] 的次序也是最优的。即要全局最优,子结构也需要最优。矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
最优子结构性质是可以使用动态规划算法求解的显著特征。
状态转移方程
设计算A[i:j](1≤i≤j≤n) 所需要的最少数乘次数为m[i,j],则原问题的最优值为m[1,n];记 Ai 的维度为 pi−1∗pi
当i==j 时,A[i:j] 即Ai 本身,因此,m[i,i]=0;(i=1,2,…,n)
当i<j 时有:
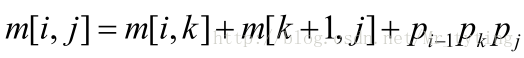
k 遍历(i,j),找到一个使得计算量最小的k,也即是:
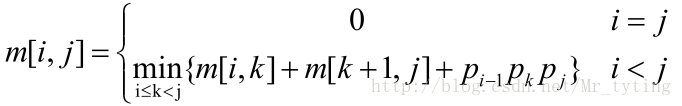
i 不断从1 扩展到 n,j 从i 扩展,随着问题规模越来越大,总能求出 m[1,n]。
实现代码
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
using namespace std;
//p[0,..,n]存储n+1个数,其中(p[i-1],p[i])是矩阵i的阶
//s[i][j]记录了矩阵i连乘到矩阵j应该在哪断开;m[i][j]记录了矩阵i连乘到矩阵j最小计算量
void MatrixMultiply(int* p, int n, int** m, int** s)
{
int r, i, j, k, t;
for (i = 1; i <= n; i++)
m[i][i] = 0;
//r个连续矩阵相乘,r不断扩展,不断计算任意两点之间最优断开点,最小计算量
for (r = 2; r <= n; r++)
{
for (i = 1; i <= n - r + 1; i++)
{
j = i + r - 1;
m[i][j] = m[i][i]+m[i + 1][j] + p[i - 1] * p[i] * p[j];//初始值,第一项m[i][i]=0
s[i][j] = i;//初始在i处断开
for (k = i + 1; k < j; k++)
{
t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k]*p[j];
if (t < m[i][j])
{
m[i][j] = t;//(i,j)最小计算量
s[i][j] = k;//记录(i,j)中最优断开点
}
}
}
}
}找零钱问题
问题描述
给定某不超过100 万元的现金总额,兑换成数量不限的100、50、20、10、5、2、1 的组合,共有多少种组合 呢?注意这里问的是多少种组合问题分析
此问题涉及两个类别:面额和总额。如果面额都是1 元的,则无论总额多少,可行的组合数显然都为1。
如果面额多一种,则组合数有什么变化呢?
定义dp[i][j]:使用面额小于等于 i 的钱币,凑成j 元钱,共有多少种组合方法。
dp[100][500]=dp[50][500]+dp[100][400]
dp[50][500]:50 以下的面额的组成500 是一种组合方式,这里面就包括了dp[20][500],dp[10][500]等
dp[100][400]:表示首先拿出100 的面额,剩余的 400 用小于等于100 的面额组合。
上述两种组合方式没有包含关系,两种组合合在一起组成所有的组合方式。
dp[i][j]=dp[ismall][j]+dp[i][j−i]
如果把 i 看成数组下标,则有:dp[i][j]=dp[i−1][j]+dp[i][j−dom[i]]
递推公式
使用dom[]=1,2,5,10,20,50,100 表示基本面额,i 的意义从面额变成面额下标,则: dp[i][j]=dp[i−1][j]+dp[i][j−dom[i]]从而有:
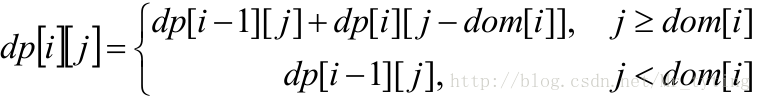
初始条件( 注意都为1,而不是0):
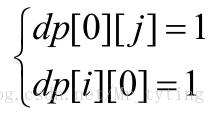
按照上面的状态转移方差我们可以从初始状态一直推导到终止状态dp[6][100w]
实现代码
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
using namespace std;
int Charge(int value, const int* denomination, int size)
{
int i;//i是下标
int** dp = new int*[size];//dp[i][j]:用i面额以下的组合成j元
for (i = 0; i < size; i++)
dp[i] = new int[value + 1];
int j;
for (j = 0; j <= value; j++)//i=0表示用面额1元的
dp[0][j] = 1;//这个时候只有一种组合方式
for (i = 1; i < size; i++)//先用面额小的,再用面额大的
{
dp[i][0] = 1;//添加任何一种面额,都是一种组合
for (j = 1; j <= value; j++)//先组合小的,然后扩展,在小的基础上一直组合到dp[size-1][value]
{
if (j >= denomination[i])
dp[i][j] = dp[i-1][j]+dp[i][j-denomination[i]];
else
dp[i][j] = dp[i - 1][j];
}
}
int time = dp[size - 1][value];
//清理内存
for (i = 0; i < size; i++)
delete[] dp[i];
return time;
}
int main()
{
int denomination[] = { 1, 2, 5, 10, 20, 50, 100 };
int size = sizeof(denomination) / sizeof(int);
int value = 200;
int c = Charge(value, denomination, size);
cout << c << endl;
return 0;
}滚动数组
将状态转移方程去掉第一维,很容易使用滚动数组,降低空间使用量。原状态转移方程:
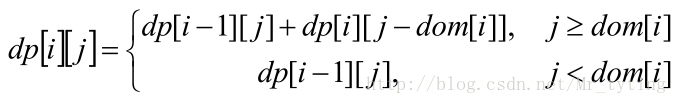
滚动数组版本的状态转移方程:

这个 last[j] 就是原始状态转移方程中的dp[i−1][j] 。dp[j] 就是dp[i][j]。
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
int Charge2(int value, const int* denomination, int size)
{
int i;//i是下标
int* dp = new int[value+1];//dp[i][j]:用i面额以下的组合成j元
int* last = new int[value + 1];
int j;
for (j = 0; j <= value; j++)//只用面额1元的
{
dp[j] = 1;
last[j] = 1;
}
for (i = 1; i < size; i++)
{
for (j = 1; j <= value; j++)
{
if (j >= denomination[i])
dp[j] = last[j] + dp[j - denomination[i]];
}
memcpy(last, dp, sizeof(int)*(value + 1));//相当于dp[i-1][j] 赋值给last
}
int times = dp[value];
delete[] last;
delete[] dp;
return times;
}
int main()
{
int denomination[] = { 1, 2, 5, 10, 20, 50, 100 };
int size = sizeof(denomination) / sizeof(int);
int value = 200;
int c = Charge2(value, denomination, size);
cout << c << endl;
return 0;
}在动态规划的问题中,如果不求具体解的内容,而只是求解的数目,往往可以使用滚动数组的方式降低空间使用量(甚至空间复杂度),由于滚动数组减少了维度,甚至代码会更简单,但是代码会更加难以理解。
走棋盘/格子取数
问题描述
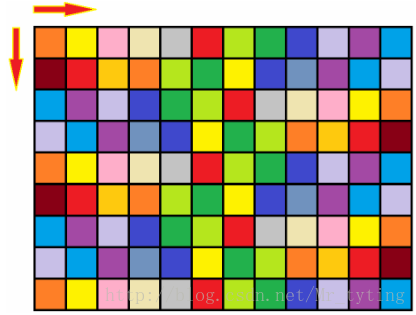
给定 m×n 的矩阵,每个位置是有一个非负整数的权值,从左上角开始,每次只能朝右和下走,走到右下角,求总和最小的权值。
状态转移方程
走的方向决定了同一个格子不会经过两次。若当前位于(x,y) 处,它来自于哪些格子呢?
dp[x,y] 表示从起点走到坐标为(x,y) 的方格的最小权值。
dp[0,0]=a[0,0], 第一行(列)累积
dp[x,y]=min(dp[x−1,y]+a[x,y],dp[x,y−1]+a[x,y])
即:dp[x,y]=min(dp[x−1,y],dp[x,y−1])+a[x,y]
状态转移方程:
⎧⎩⎨⎪⎪dp(i,0)=∑ik=0chess[k][0]dp(0,j)=∑jk=0chess[0][k]dp(i,j)=min(dp(i−1,j),dp(i,j−1))+chess[i][j]
在上边界时只能向右走,在左边界时只能向下走。
滚动数组去除第一维:{dp(j)=∑ik=0chess[0][k]dp(0,j)=min(dp(j),dp(j−1))+chess[i][j]
实现代码
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int MinPath(vector<vector<int>> &chess, int M, int N)
{
vector<int> pathLength(N);
int i, j;
//初始化
pathLength[0] = chess[0][0];
for (j = 1; j < N; j++)
pathLength[j] = pathLength[j - 1] + chess[0][j];
//依次计算每行
for (i = 1; i < M; i++)
{
pathLength[0] += chess[i][0];
for (j = 1; j < N; j++)
{
if (pathLength[j - 1] < pathLength[j])
pathLength[j] = pathLength[j - 1] + chess[i][j];
else
pathLength[j] += chess[i][j];
}
}
return pathLength[N - 1];
}
int main()
{
const int M = 10;
const int N = 8;
vector<vector<int>> chess(M, vector<int>(N));
//初始化棋盘(随机给定)
int i, j;
for (i = 0; i < M; i++)
{
for (j = 0; j < N; j++)
chess[i][j] = rand() % 100;
}
cout << MinPath(chess, M, N) << endl;
return 0;
}带陷阱的走棋盘问题
问题分析
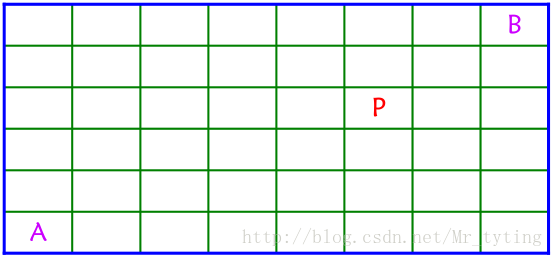
在8×6 的矩阵中,每次只能向上或向右移动一格,并且不能经过P 。试计算从A 移动到B 一共有多少种走法。
状态转移方程
dp[i][j] 表示从起点到(i,j) 的路径条数。只能从左边或者上边进入一个格子。
如果 (i,j) 被占用,dp[i][j]=0
如果(i,j) 不被占用,dp[i][j]=dp[i−1][j]+dp[i][j–1]
故状态转移方程:⎧⎩⎨dp[i][0]=dp[0][j]=1dp[i][j]=0dp[i][j]=dp[i−1][j]+dp[i][j−1](i=0||j=0)(i,j)被占用(i,j)没被占用
一共要走m+n–2 步,其中(m–1) 步向右,(n−1) 步向下。组合数C(m+n–2,m−1)=C(m+n−2,n−1)
问题解决

我们把 A 点看着起点 (0,0) ,计算起点A 到终点 B 的所有路径allPath,然后再计算 A 到 p 的所有路径path1 ,再计算p 到B 的所有路径paht2 ,那么paht1∗path2 即是从起点 A 到终点B 的所有经过点 p 的路径数,allPath−paht1∗paht2 即为避开点p 从A 到点B 的所有路径。
实现代码
#include<stdio.h>
#include <stdlib.h>
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int MinPath(vector<vector<int>> dp,int M, int N)
{
int i, j;
//在左边界和下边界上的点路径都只有1
for (i = 0; i < M+1; i++)
dp[i][0] = 1;
for (j = 0; j < N+1; j++)
dp[0][j] = 1;
for (i = 1; i < M+1; i++)
{
for (j = 1; j < N+1; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[M]
;
}
int main()
{
const int M = 6;
const int N = 8;
vector<vector<int>> dp(M, vector<int>(N));
int x = 3;
int y = 5;
int allPath = MinPath(dp,M-1, N-1);//从起点到终点的所有路径
int path1 = MinPath(dp,x, y);//起点到占用点所有路径
int path2 = MinPath(dp, M-x-1, N-y-1);//从占用点到终点的所有路径
int path = allPath - path1*path2;//在所有路径中除去经过占用点路径数
cout << path << endl;
return 0;
}动态规划总结

动态规划是方法论,是解决一大类问题的通用思路。事实上,很多内容都可以归结为动态规划的思想。
何时可以考虑使用动态规划:
初始规模下能够方便的得出结论
空串、长度为0的数组、自身等’
能够得到问题规模增大导致的变化
递推式——状态转移方程
在实践中往往忽略无后效性
哪些题目不适合用动态规划?
状态转移方程 的推导,往往陷入局部而忽略全局。在重视动态规划的同时,别忘了从总体把握问题。
相关文章推荐
- 贪心算法 & 动态规划基础题
- 贪心算法基础
- 贪心算法--1基础
- [Coursera]算法基础_Week5_动态规划(2)_Q1
- 五大常用经典算法(分治、动态规划、贪心、回溯、分支限界)
- 计算机算法基础--贪心-有限期作业排序--更详细证明
- 五类常见算法小记 (递归与分治,动态规划,贪心,回溯,分支界限法)
- 动态规划1-数字三角形(算法基础 第4周)
- 五大常用算法:分治、动态规划、贪心、回溯和分支界定
- RSA算法基础->实践
- 基础算法之贪心算法
- 51nod 完美字符串(贪心算法基础)
- 五大常用算法:分治、动态规划、贪心、回溯、分支限界
- 贪心算法-分治算法-动态规划-回溯-分支限界的简单介绍
- [Coursera]算法基础_Week5_动态规划(2)_Q2
- RSA算法基础->实践
- iOS开发基础笔记-算法<三>
- 二分与贪心-Yogurt factory(算法基础 第9周)
- <算法导论>学习笔记(2)--第2章 算法基础
- 五类常见算法小记 (递归与分治,动态规划,贪心,回溯,分支界限法)
