计算几何基础(学习中)
2017-08-20 20:58
387 查看

[pixiv] https://www.pixiv.net/member_illust.php?mode=medium&illust_id=60959813
(国服挺住啊Q^Q)
计算几何基础 基本运算 基础类 点积 叉积 线 直线与线段的表示 直线求交 线段判交 多边形 求多边形的重心 判定点在多边形内 求多边形的面积 常用算法 凸包 半平面交
基本运算
基础类
struct Vec{//既可以存点,也可以存向量
double x, y;
double len(){
return sqrt (x * x + y * y);
}
};
Vec operator+(const Vec &a, const Vec &b){
Vec c;
c.x = a.x + b.x, c.y = a.y + b.y;
return c;
}
Vec operator-(const Vec &a, const Vec &b){
Vec c;
c.x = a.x - b.x, c.y = a.y - b.y;
return c;
}
Vec operator*(double s, const Vec &a){
Vec c;
c.x = a.x * s, c.y = a.y * s;
return c;
}
Vec operator/(const Vec &a, double s){
Vec c;
c.x = a.x / s, c.y = a.y / s;
return c;
}点积
正负:正,夹角小于90° 负,夹角大于90°double dot(const vec &x, const vec &s){
return r.x * s.x + r.y * s.y;
}叉积
几何意义:两向量所形成的平行四边形的面积正负:正,→y在→x左边 负,右边
double cross(const vec &x, const vec &y){
return r.x * s.y - r.y * s.x;
}点积与叉积结合起来,可以判断两向量的位置(指如图)关系
| | -------------- | |
线
直线与线段的表示
直线:一个其上的点P,及方向向量→u来表示线段:1、两个端点 2、一个端点,一个向量(准确指向另一端点)
直线求交
两个直线(P,→u),(Q,→v),可知交点S=P+t*→u。求出t可用等面积法vec line_intersect(point P, vec u, point Q, vec v){
double t = cross(Q - P, v) / cross(u, v);
return P + u * t;
}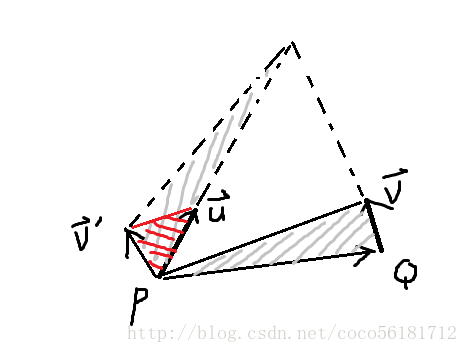
图片很直观吧【滑稽
至于正负问题,讨论一下就发现没问题了。但是要千万记得顺序,可以用图来辅助记忆
线段判交
跨立实验bool seg_intersect (Point A, Point B, Point C, Point D) {
double c1 = cross(Line(A,B),Line(A,C)), c2 = cross(Line(A,B),Line(A,D));
double c3 = cross(Line(C,D),Line(C,A)), c4 = cross(Line(C,D),Line(C,B));
return sign(c1) * sign(c2) < 0 && sign(c3) * sign(c4) < 0;
}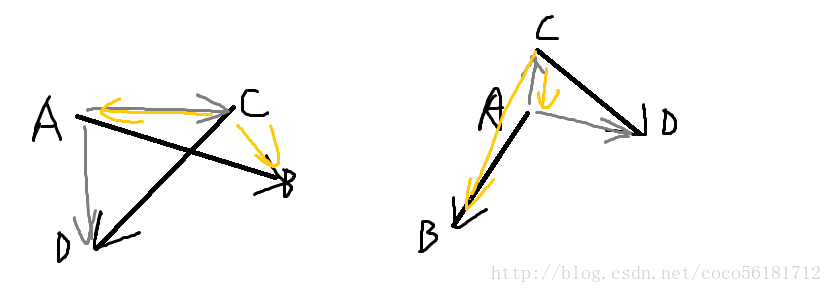
这里主要运用了叉积判断左右的性质。我们可以感性的理解到,若线段相交,自己的端点肯定在对方的两侧,不相交则至少有一个不满足。
多边形
求多边形的重心
我们需要两个基础1、三角形的重心求法(数学课上学过啦)
2、(∑→v * m0)/M (找一个点为原点,则多边形内每一个点都有一个向量和质量)
感性理解一下,我们可以通过分治的思想,发现已知图形两个部分的重心和质量(面积)→P1、S1和→P2、S2,则→P=(→P1 * S1 + →P2 * S2)/(S1+S2)
因为任意一个多边形可以拆分成若干个三角形,所以根据以上两个基础就可以进行两两合并知道求出重心为止。
判定点在多边形内
如果一个点在多边形内,从这个点拉一条射线出去,必定会穿过边。然而点不在多边形内,也有可能穿过边,但是它必定还会穿出去,所以经过的边数必为偶数,在内部的必为奇数。这里把模型稍微改一下。我们给多边形的每一条边一个方向,统一顺时针或逆时针(存的时候就是有方向的啊)。向上+1,向下-1(反之也行)
看代码理解一下
bool point_on_line (const Point &p, const Point &A, const Point &B) {
return sign(cross(B-A, p-A)) == 0 && sign(dot(A-p,B-p)) <= 0;
}
bool in_polygon (const Point &p, const vector<Point> &poly) {
int n = (int)poly.size();
int counter = 0;
for (int i = 0; i < n; ++i) {
Point a = poly[i], b = poly[(i + 1) % n];
if (point_on_line (p, a, b)) return true; // bounded included
int x = sign(cross(p - a, b - a));
int y = sign(a.y - p.y);
int z = sign(b.y - p.y);
if (x > 0 && y <= 0 && z > 0) counter++;
if (x < 0 && z <= 0 && y > 0) counter--;
}
return counter != 0;
}画图理解一下就记住了,画图现推也行
求多边形的面积
主要利用了叉积的几何意义及正负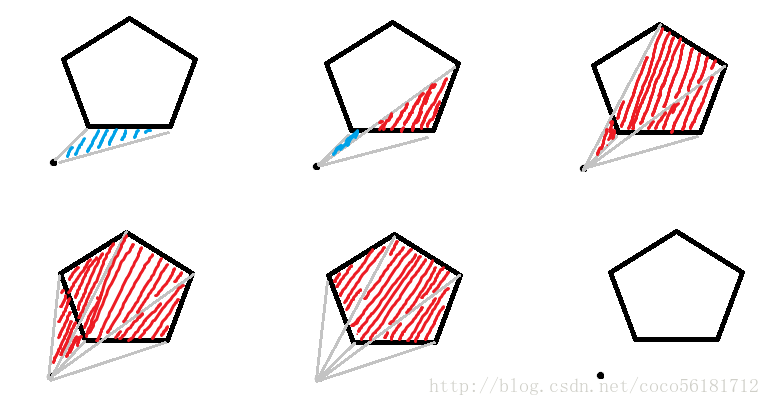
很直观吧
double area(const vector<Point> &poly) {
double rt = 0.0;
int n = (int)poly.size();
for(int i = 0; i < n; i++) {
rt += cross(poly[i], poly[(i+1)%n]);
}
return fabs(rt / 2.0);
}常用算法
凸包
凸包的定义:将一堆点包括进去的最小的凸多边形求凸包:模拟绳子绕钉子的模型
void get_convex(){
sort(point + 1, point + cntp + 1, cmp);
for(int i = 1; i <= cntp; i++){
while(top > 1 && (cross(point[i] - stack[top-1], stack[top] - stack[top-1]) > 0))
top--;
stack[++top] = point[i];
}
int tmp = top;
for(int i = cntp-1; i >= 1; i--){
while(top > tmp && (cross(point[i] - stack[top], stack[top] - stack[top-1]) > 0))
top--;
stack[++top]=point[i];
}
if(cntp > 1) top--;
}半平面交
(还在学习中。。。)相关文章推荐
- AIZU OJ 2308 基础计算几何学习
- 计算几何基础(学习中)
- POJ1269---Intersecting Lines (计算几何基础:直线相交求交点)
- 分布式基础学习【二】 —— 分布式计算系统(Map/Reduce)
- ACM学习历程—HDU1392 Surround the Trees(计算几何)
- 关于计算几何某些定理·基础知识的汇总
- 计算广告学习笔记1.3 广告的基础知识-广告与营销的区别
- 黑马程序员之C#编程基础学习笔记:用while计算1到100之间整数的和;
- Segments(计算几何基础)
- 【笔记篇】最良心的计算几何学习笔记(一)
- 计算几何基础模板 以后还会更新
- ACM学习历程—HDU4720 Naive and Silly Muggles(计算几何)
- Training:计算几何基础
- matlab基础学习——数值计算
- 计算几何基础
- BZOJ_1610_[Usaco2008_Feb]_Line连线游戏_(计算几何基础+暴力)
- 【笔记篇】最良心的计算几何学习笔记(六)
- 计算几何学习笔记之点和直线
- POJ 1556 计算几何基础
- 【学习笔记】3D图形核心基础精炼版-5:stage3D实战-矩阵计算
