Dinic最大流(bzoj 2756: [SCOI2012]奇怪的游戏)
2017-07-31 22:04
549 查看
Dinic算法:
转一张很好懂的图,复杂度O(V²E)
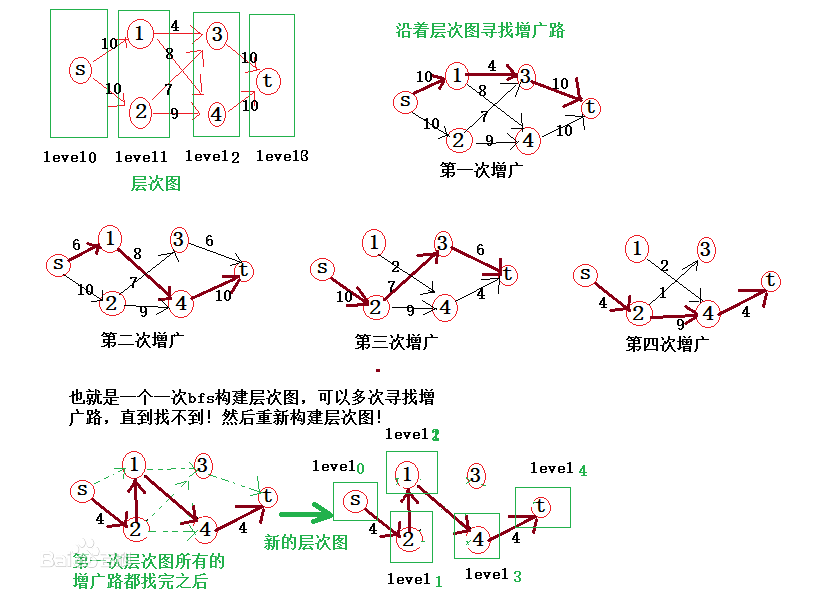
注意一开始的那个层次图并不是原图,是第一次bfs时所保留的边
(像原图中1和2之间也有一条边,不过第一次bfs时这条边并不会被经过)
Submit: 3962 Solved: 1099
[Submit][Status][Discuss]
这个游戏在一个 N*M 的棋盘上玩,每个格子有一个数。每次 Blinker 会选择两个相邻
的格子,并使这两个数都加上 1。
现在 Blinker 想知道最少多少次能使棋盘上的数都变成同一个数,如果永远不能变成同
一个数则输出-1。
每轮游戏的第一行有两个整数N和M, 分别代表棋盘的行数和列数。
接下来有N行,每行 M个数。
2 2
1 2
2 3
3 3
1 2 3
2 3 4
4 3 2
-1
显而易见的网络流
先将格子分类
如果格子坐标(x, y)满足x+y为偶数,那么称为A类格子,否则成为B格子
这样AB格子一定是交错的
然后就可以建图了,假设最后棋盘上所有数字都能变成x,那么
源点向所有A类格子都连接一条流量为x-a[x][y]的边
所有B类格子向汇点都连接一条流量为x-a[x][y]的边
若有A类格子向它相邻的B类格子连接一条流量为无穷大的边
求出来的最大流一定满流
所以只要暴力枚举x看什么时候满流就好了
等等,这样不是超时定了,x的范围甚至超过int
那继续分析
假设所有A格子的个数是numA,B格子个数是numB
A类格子上数字之和为sumA,B类格子上数字之和为sumB,
很显然每次操作一定是将sumA和sumB同时+1
所以这样假设最中所有数字都能变成x,则一定有
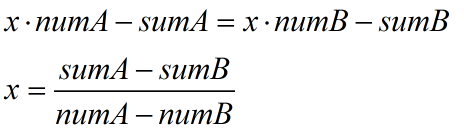
这样当numA!=numB时,x的取值只有一种可能
只要判断①对应网络是否满流②它是否大于等于棋盘中最大的数即可
当numA==numB时,如果sumA!=sumB,那么一定无解
sumA==sumB的话,如果x合法,那么x+1也一定合法(因为棋盘的格子数量为偶数个,直接平铺就好了)
所以x具有二分性质
二分x即可,下限是棋盘中最大的数,上限可能非常非常大,所以一定要设一个很大很大的数
这题每次只增广一条路的话貌似会超时?所以用dinic吧
转一张很好懂的图,复杂度O(V²E)

注意一开始的那个层次图并不是原图,是第一次bfs时所保留的边
(像原图中1和2之间也有一条边,不过第一次bfs时这条边并不会被经过)
2756: [SCOI2012]奇怪的游戏
Time Limit: 40 Sec Memory Limit: 128 MBSubmit: 3962 Solved: 1099
[Submit][Status][Discuss]
Description
Blinker最近喜欢上一个奇怪的游戏。这个游戏在一个 N*M 的棋盘上玩,每个格子有一个数。每次 Blinker 会选择两个相邻
的格子,并使这两个数都加上 1。
现在 Blinker 想知道最少多少次能使棋盘上的数都变成同一个数,如果永远不能变成同
一个数则输出-1。
Input
输入的第一行是一个整数T,表示输入数据有T轮游戏组成。每轮游戏的第一行有两个整数N和M, 分别代表棋盘的行数和列数。
接下来有N行,每行 M个数。
Output
对于每个游戏输出最少能使游戏结束的次数,如果永远不能变成同一个数则输出-1。Sample Input
22 2
1 2
2 3
3 3
1 2 3
2 3 4
4 3 2
Sample Output
2-1
显而易见的网络流
先将格子分类
如果格子坐标(x, y)满足x+y为偶数,那么称为A类格子,否则成为B格子
这样AB格子一定是交错的
然后就可以建图了,假设最后棋盘上所有数字都能变成x,那么
源点向所有A类格子都连接一条流量为x-a[x][y]的边
所有B类格子向汇点都连接一条流量为x-a[x][y]的边
若有A类格子向它相邻的B类格子连接一条流量为无穷大的边
求出来的最大流一定满流
所以只要暴力枚举x看什么时候满流就好了
等等,这样不是超时定了,x的范围甚至超过int
那继续分析
假设所有A格子的个数是numA,B格子个数是numB
A类格子上数字之和为sumA,B类格子上数字之和为sumB,
很显然每次操作一定是将sumA和sumB同时+1
所以这样假设最中所有数字都能变成x,则一定有
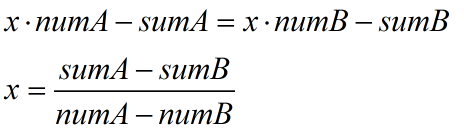
这样当numA!=numB时,x的取值只有一种可能
只要判断①对应网络是否满流②它是否大于等于棋盘中最大的数即可
当numA==numB时,如果sumA!=sumB,那么一定无解
sumA==sumB的话,如果x合法,那么x+1也一定合法(因为棋盘的格子数量为偶数个,直接平铺就好了)
所以x具有二分性质
二分x即可,下限是棋盘中最大的数,上限可能非常非常大,所以一定要设一个很大很大的数
这题每次只增广一条路的话貌似会超时?所以用dinic吧
#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<queue>
#define LL long long
using namespace std;
LL n, m, cnt, S, T, a[45][45], head[2005], h[2005], cur[2005], dir[4][2] = {1,0,0,1,-1,0,0,-1};;
typedef struct
{
LL to, next;
LL flow;
}Road;
Road G[20005];
void Add(LL u, LL v, LL flow)
{
cnt++;
G[cnt].next = head[u];
head[u] = cnt;
G[cnt].to = v;
G[cnt].flow = flow;
}
int Jud()
{
LL now, i;
queue<int> q;
memset(h, -1, sizeof(h));
q.push(S);
h[S] = 0;
while(q.empty()==0)
{
now = q.front();
q.pop();
for(i=head[now];i!=0;i=G[i].next)
{
if(G[i].flow && h[G[i].to]==-1)
{
h[G[i].to] = h[now]+1;
q.push(G[i].to);
}
}
}
if(h[T]!=-1)
return 1;
return 0;
}
LL Sech(LL x, LL flow) //每次传入的flow是能经经过当前节点的最大流量
{
LL w, used, i;
if(x==T)
return flow;
used = 0;
for(i=cur[x];i!=0;i=G[i].next)
{
if(h[G[i].to]==h[x]+1)
{
w = Sech(G[i].to, min(flow-used, G[i].flow));
G[i].flow -= w;
G[i^1].flow += w;
if(G[i].flow)
cur[x] = i;
used += w;
if(used==flow) //如果当前节点都已经满流了,就没必要再往下搜了
return flow;
}
}
if(used==0) //如果经过这个点的水流没有一滴都到达汇点,这给点已经无法再增广,屏蔽
h[x] = -1;
return used;
}
LL Dinic()
{
LL i, flow = 0;
while(Jud())
{
for(i=S;i<=T;i++)
cur[i] = head[i];
flow += Sech(S, (LL)1<<50);
}
return flow;
}
int Check(LL x)
{
LL i, j, dx, dy, k, full;
S = 0, T = n*m+1, cnt = 1;
memset(head, 0, sizeof(head));
full = 0;
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if((i+j)%2==0)
{
Add(S, (i-1)*m+j, x-a[i][j]);
Add((i-1)*m+j, S, 0);
full += x-a[i][j];
for(k=0;k<=3;k++)
{
dx = i+dir[k][0];
dy = j+dir[k][1];
if(dx<1 || dy<1 || dx>n || dy>m)
continue;
Add((i-1)*m+j, (dx-1)*m+dy, (LL)1<<50);
Add((dx-1)*m+dy, (i-1)*m+j, 0);
}
}
else
{
Add((i-1)*m+j, T, x-a[i][j]);
Add(T, (i-1)*m+j, 0);
}
}
}
if(Dinic()==full)
return 1;
return 0;
}
int main(void)
{
LL T, i, j, sa[2], sb[2], l, r, mid, temp;
scanf("%lld", &T);
while(T--)
{
l = 0, r = (LL)1<<50;
sa[1] = sb[1] = sa[0] = sb[0] = 0;
scanf("%lld%lld", &n, &m);
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
scanf("%lld", &a[i][j]);
if((i+j)%2)
sb[0]++, sb[1] += a[i][j];
else
sa[0]++, sa[1] += a[i][j];
l = max(l, a[i][j]);
}
}
if(sa[0]!=sb[0])
{
temp = (sb[1]-sa[1])/(sb[0]-sa[0]);
if(temp>=l && Check(temp))
printf("%lld\n", temp*sa[0]-sa[1]);
else
printf("-1\n");
}
else
{
if(sa[1]!=sb[1])
printf("-1\n");
else
{
while(l<r)
{
mid = (l+r)/2;
if(Check(mid))
r = mid;
else
l = mid+1;
}
printf("%lld\n", l*sa[0]-sa[1]);
}
}
}
return 0;
}
相关文章推荐
- 【BZOJ 2756】[SCOI2012]奇怪的游戏 二分+最大流
- 【bzoj2756】【SCOI2012】【奇怪的游戏】【最大流+二分】
- BZOJ 2756 SCOI 2012 奇怪的游戏 二分+最大流
- 【BZOJ2756】【SCOI2012】奇怪的游戏 最大流、
- bzoj 2756 [SCOI2012]奇怪的游戏【二分+最大流】
- BZOJ 2756: [SCOI2012]奇怪的游戏 [最大流 二分]
- 【二分+最大流】[SCOI2012]奇怪的游戏 BZOJ2756
- bzoj2756: [SCOI2012]奇怪的游戏 二分+最大流
- 【最大流】【二分】[Scoi2012] bzoj2756 奇怪的游戏
- BZOJ2756 [SCOI2012]奇怪的游戏 【网络流 + 二分】
- bzoj2756: [SCOI2012]奇怪的游戏
- BZOJ2756 [SCOI2012]奇怪的游戏 【网络流 + 二分】
- bzoj2756 [SCOI2012]奇怪的游戏
- 【SCOI2012】bzoj2756 奇怪的游戏
- BZOJ 2756: [SCOI2012]奇怪的游戏 网络流/二分
- bzoj2756: [SCOI2012]奇怪的游戏
- BZOJ2756: [SCOI2012]奇怪的游戏(网络流)(还差代码)
- BZOJ2756 【scoi2012】奇怪的游戏(二分+网络流)
- BZOJ 2756 [SCOI2012]奇怪的游戏 二分+网络流
- BZOJ 2756: [SCOI2012]奇怪的游戏
