最大似然估计(MLE)与最大后验估计(MAP)
2017-07-17 16:37
232 查看
转载自:http://www.cnblogs.com/sylvanas2012/p/5058065.html
1) 最大似然估计 MLE
给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即“模型已定,参数未知”。例如,我们知道这个分布是正态分布,但是不知道均值和方差;或者是二项分布,但是不知道均值。 最大似然估计(MLE,Maximum Likelihood Estimation)就可以用来估计模型的参数。MLE的目标是找出一组参数,使得模型产生出观测数据的概率最大:
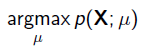
其中
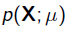
就是似然函数,表示在参数

下出现观测数据的概率。我们假设每个观测数据是独立的,那么有
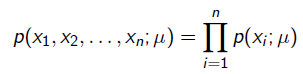
为了求导方便,一般对目标取log。 所以最优化对似然函数等同于最优化对数似然函数:
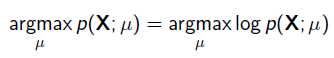
举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币,如果正面朝上记为H,方面朝上记为T,抛10次的结果如下:
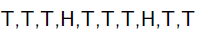
求这个硬币正面朝上的概率有多大?
很显然这个概率是0.2。现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布,设正面朝上的概率是

,那么似然函数为:
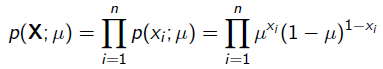
x=1表示正面朝上,x=0表示方面朝上。那么有:
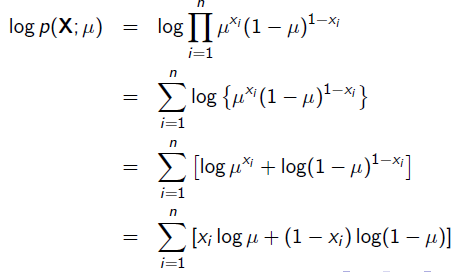
求导:
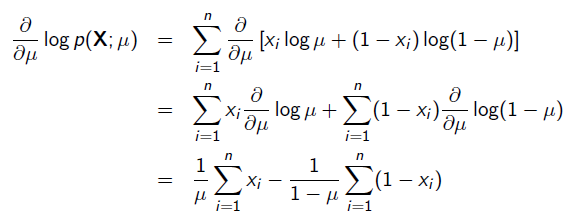
令导数为0,很容易得到:
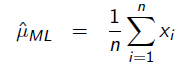
也就是0.2 。
2) 最大后验概率 MAP
以上MLE求的是找出一组能够使似然函数最大的参数,即
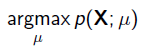
。 现在问题稍微复杂一点点,假如这个参数

有一个先验概率呢?比如说,在上面抛硬币的例子,假如我们的经验告诉我们,硬币一般都是匀称的,也就是

=0.5的可能性最大,

=0.2的可能性比较小,那么参数该怎么估计呢?这就是MAP要考虑的问题。
MAP优化的是一个后验概率,即给定了观测值后使

概率最大:
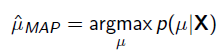
把上式根据贝叶斯公式展开:
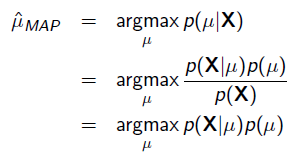
我们可以看出第一项
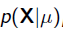
就是似然函数,第二项
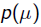
就是参数的先验知识。取log之后就是:
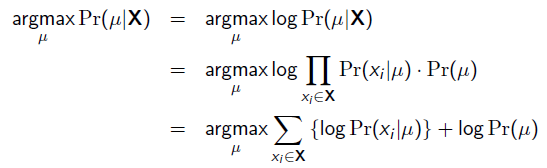
回到刚才的抛硬币例子,假设参数

有一个先验估计,它服从Beta分布,即:
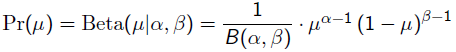
而每次抛硬币任然服从二项分布:
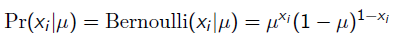
那么,目标函数的导数为:
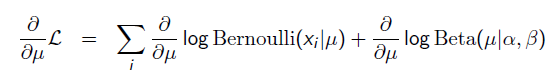
求导的第一项已经在上面MLE中给出了,第二项为:
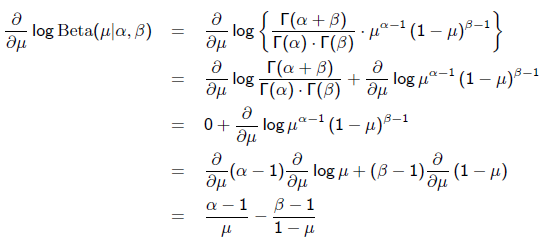
令导数为0,求解为:
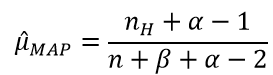
其中,
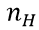
表示正面朝上的次数。这里看以看出,MLE与MAP的不同之处在于,MAP的结果多了一些先验分布的参数。
1) 最大似然估计 MLE
给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参,即“模型已定,参数未知”。例如,我们知道这个分布是正态分布,但是不知道均值和方差;或者是二项分布,但是不知道均值。 最大似然估计(MLE,Maximum Likelihood Estimation)就可以用来估计模型的参数。MLE的目标是找出一组参数,使得模型产生出观测数据的概率最大:
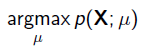
其中
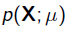
就是似然函数,表示在参数

下出现观测数据的概率。我们假设每个观测数据是独立的,那么有
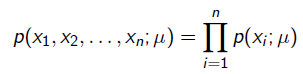
为了求导方便,一般对目标取log。 所以最优化对似然函数等同于最优化对数似然函数:
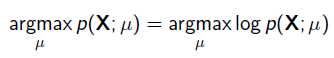
举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币,如果正面朝上记为H,方面朝上记为T,抛10次的结果如下:
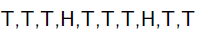
求这个硬币正面朝上的概率有多大?
很显然这个概率是0.2。现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布,设正面朝上的概率是

,那么似然函数为:
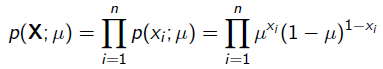
x=1表示正面朝上,x=0表示方面朝上。那么有:
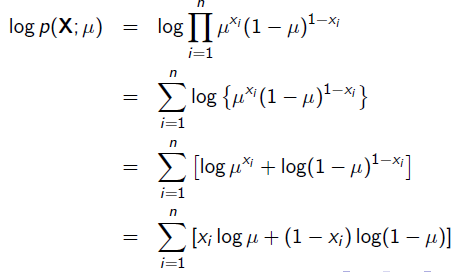
求导:
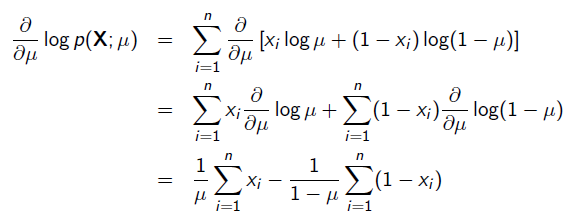
令导数为0,很容易得到:
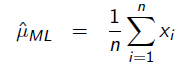
也就是0.2 。
2) 最大后验概率 MAP
以上MLE求的是找出一组能够使似然函数最大的参数,即
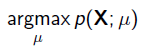
。 现在问题稍微复杂一点点,假如这个参数

有一个先验概率呢?比如说,在上面抛硬币的例子,假如我们的经验告诉我们,硬币一般都是匀称的,也就是

=0.5的可能性最大,

=0.2的可能性比较小,那么参数该怎么估计呢?这就是MAP要考虑的问题。
MAP优化的是一个后验概率,即给定了观测值后使

概率最大:
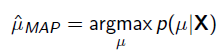
把上式根据贝叶斯公式展开:
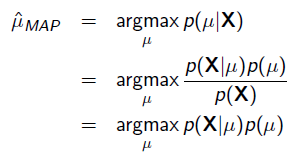
我们可以看出第一项
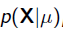
就是似然函数,第二项
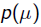
就是参数的先验知识。取log之后就是:
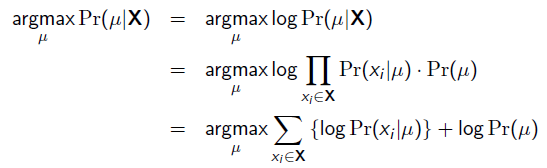
回到刚才的抛硬币例子,假设参数

有一个先验估计,它服从Beta分布,即:
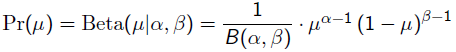
而每次抛硬币任然服从二项分布:
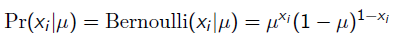
那么,目标函数的导数为:
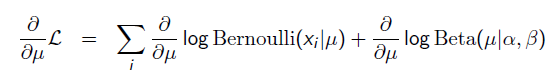
求导的第一项已经在上面MLE中给出了,第二项为:
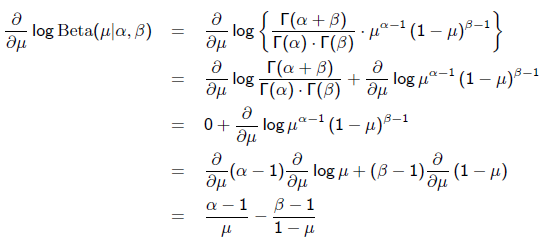
令导数为0,求解为:
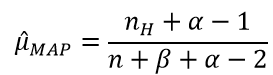
其中,
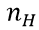
表示正面朝上的次数。这里看以看出,MLE与MAP的不同之处在于,MAP的结果多了一些先验分布的参数。
相关文章推荐
- 最大似然估计(MLE)与最大后验估计(MAP)
- 参数估计:最大似然估计(MLE),最大后验估计(MAP),贝叶斯估计,经验贝叶斯(Empirical Bayes)与全贝叶斯(Full Bayes)
- 参数估计:最大似然估计(MLE),最大后验估计(MAP),贝叶斯估计,经验贝叶斯(Empirical Bayes)与全贝叶斯(Full Bayes)
- 机器学习->统计学基础->贝叶斯估计,最大似然估计(MLE),最大后验估计(MAP)
- 最大似然估计(MLE)和最大后验概率估计(MAP)
- 最大似然估计(MLE)最大后验概率估计(MAP)以及贝叶斯公式的理解
- 机器学习->统计学基础->贝叶斯估计,最大似然估计(MLE),最大后验估计(MAP)
- 最大似然估计 (MLE)与 最大后验概率(MAP)在机器学习中的应用
- 参数估计(Parameter Estimation):频率学派(最大似然估计MLE、最大后验估计MAP)与贝叶斯学派(贝叶斯估计BPE)
- 【转载】参数估计(Parameter Estimation):频率学派(最大似然估计MLE、最大后验估计MAP)与贝叶斯学派(贝叶斯估计BPE)
- 最大似然估计(MLE)和最大后验概率(MAP)
- 详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
- 最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
- 最大似然估计 (MLE) 最大后验概率(MAP)
- 最大似然估计(MLE)和最大后验概率(MAP)
- 最大似然估计 (MLE) 最大后验概率(MAP)
- 参数估计(Parameter Estimation):频率学派(最大似然估计MLE、最大后验估计MAP)与贝叶斯学派(贝叶斯估计BPE)
- 最大似然估计(MLE)和最大后验概率(MAP)
- 最大似然估计 (MLE) 最大后验概率(MAP)
- 先验概率、最大释然估计(MLE)与最大后验估计(MAP)
