hdu 1402 A * B Problem Plus FFT模板

FFT的实现..涉及大量的数学知识..搞不来..更玄学了.....

反正FFT就是能够在O(nlogb)时间内将系数表示法转化为点值表示法，相乘后再将点值表示法转为系数表示法，然后实现卷积。

FFT过程：

两个次数界为n的多项式A（x）和B（x）相乘，输入输出均采用系数表示法。（假定n为2的幂）

1）使次数界增加一倍：A（x）和B（x）扩充为次数界为2n的多项式，并构造起系数表示。

2）求值：两次应用2n阶FFT，计算出A（x）和B（x）的长度为2n的点值表示。

3）点乘：计算多项式C(x)=A（x）*B（x）的点值表示。

4）插值：对2n个点值对应用一次FFT计算出其逆DFT，就可以构造出多项式C（x）的系数表示。

第1步和第3步需要时间为O(n)，第2步和第4步运用FFT需要时间为O(nlogn)。



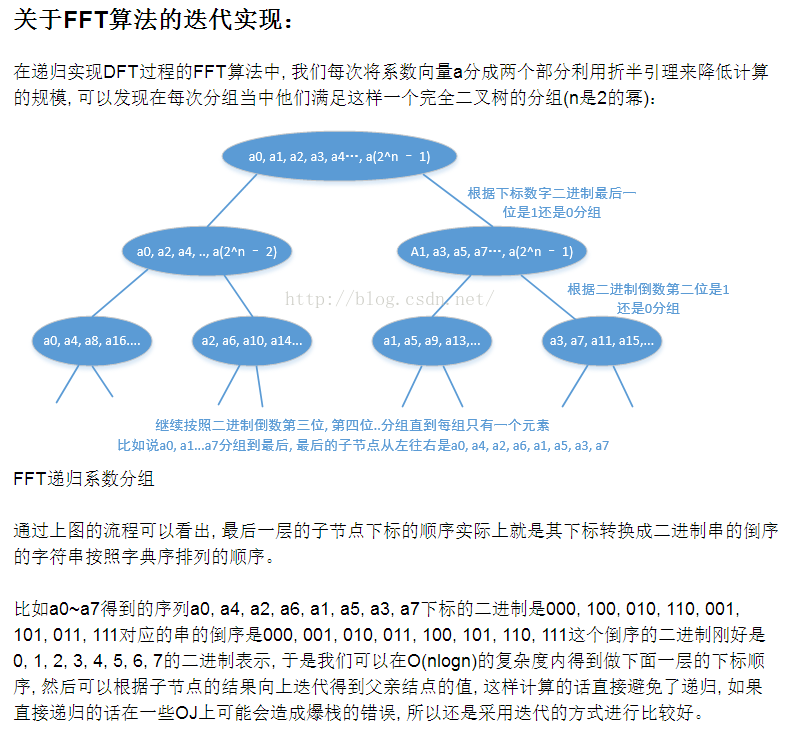
关于原理重要的就是这些了，想深入研究的可以去看ACdreamer的blog

本题是大数相乘

f(x)=a0+a1*x+a2*x^2+a3*x^3.......

g(x)=b0+b1*x+b2*x^2+b3*x^3.......

x=10 这里注意多项式的表示方式和普通我们看到的顺序是反着的

k(x)=f(x)*g(x);#include <bits/stdc++.h>
using namespace std;
#define maxn 410000
#define pi acos(-1.0)
typedef complex<double> E;
int len,n,m,L;
char st1[maxn],st2[maxn];
int R[maxn],c[maxn];
E a[maxn],b[maxn];
void fft(E *a,int f)
{
for(int i=0;i<len;i++)if(i<R[i])swap(a[i],a[R[i]]);
for(int i=1;i<len;i<<=1)
{
E wn(cos(pi/i),f*sin(pi/i));
for(int j=0;j<=len;j+=(i<<1))
{
E w(1,0);
for(int k=0;k<i;k++,w*=wn)
{
E x=a[j+k],y=a[j+k+i];
a[j+k]=x+w*y;
a[j+k+i]=x-w*y;
}
}
}
if(f==-1) for(int i=0;i<=len;i++) a[i]/=len;
}
int main()
{
while(scanf("%s%s",st1,st2)==2)
{
int l1,l2;
l1=strlen(st1);l2=strlen(st2);
l1--;l2--;////////////////////////////////下标都是从0开始
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
///////////////////////////////////////////////注意是反序
for(int i=0;i<=l1;i++) a[i]=st1[l1-i]-'0';

for(int i=0;i<=l2;i++) b[i]=st2[l2-i]-'0';

m=l1+l2;
L=0; for(len=1;len<=m;len<<=1)L++;//len为大于m的2的n次幂 为点表示法长度

for(int i=0;i<len;i++) R[i] = (R[i>>1]>>1)|((i&1)<<(L-1));

fft(a,1);fft(b,1);
for(int i=0;i<=len;i++) a[i]=a[i]*b[i];

fft(a,-1);
for(int i=0;i<=m;i++) c[i]=(int)(a[i].real()+0.1);
for(int i=0;i<=m;i++)
if(c[i]>=10)
{
c[i+1]+=c[i]/10;
c[i]%=10;
if(i==m) m++;
}

while(!c[m]&&m) m--;

for(int i=m;i>=0;i--)printf("%d",c[i]);
puts("");
}
return 0;
}