pearson 相关系数 & 机器学习模型中不平衡样本问题
2017-07-05 17:47
597 查看
0 前言:本文讨论一下几点:
1, pearson 相关系数(Pearson Correlation Coeffient) --- 皮尔逊相关系数
2,信息增益(InfoGain) 、卡方检验 与特征选择
3,机器学习模型中不平衡样本问题
1,pearson 相关系数(Pearson Correlation Coeffient) --- 皮尔逊相关系数:
(1)皮尔逊相关系数的适用范围:
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
1). 两个变量之间是线性关系,都是连续数据。
2). 两个变量的总体是正态分布,或接近正态的单峰分布。
3). 两个变量的观测值是成对的,每对观测值之间相互独立。
(2)定义:
第一种形式(也就是定义的形式):
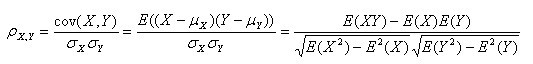
其变形(第二种形式):
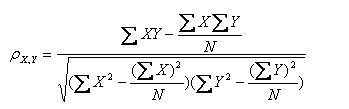
(其中,E为数学期望或均值,N为数据的数目,E{
[X-E(X)] [Y-E(Y)]}称为随机变量X与Y的协方差,记为Cov(X,Y))
(3)代码实现:
2,机器学习模型中不平衡样本问题
(1)为什么不平衡学习
传统的学习方法以降低总体分类精度为目标,将所有样本一视同仁,同等对待,造成了分类器在多数类的分类精度较高而在少数类的分类精度很低。
机器学习模型都有一个待优化的损失函数,以我们最常用最简单的二元分类器逻辑回归为例,逻辑回归以优化总体的精度为目标,
不同类别的误分类情况产生的误差是相同的,考虑一个$500:1$的数据集,即使把所有样本都预测为多数类其精度也能达到$500/501$之高,
很显然这并不是一个很好的学习效果,因此传统的学习算法在不平衡数据集中具有较大的局限性。
(2)解决方案:
解决方法主要分为两个方面,第一种方案主要从数据的角度出发,主要方法为抽样,可以通过某种策略进行抽样,让我们的数据相对均衡一些;
第二种方案从算法的角度出发,考虑不同误分类情况代价的差异性对算法进行优化。

另外可以参考 另外一篇文章
3,信息增益与特征选择
(1) 知乎上综述:
特征选择是特征工程中的重要问题(另一个重要的问题是特征提取),坊间常说:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
由此可见,特征工程尤其是特征选择在机器学习中占有相当重要的地位。
通常而言,特征选择是指选择获得相应模型和算法最好性能的特征集,工程上常用的方法有以下:
1. 计算每一个特征与响应变量的相关性:工程上常用的手段有计算皮尔逊系数和互信息系数,皮尔逊系数只能衡量线性相关性而互信息系数能够很好地度量各种相关性,
但是计算相对复杂一些,好在很多toolkit里边都包含了这个工具(如sklearn的MINE),得到相关性之后就可以排序选择特征了;
2. 构建单个特征的模型,通过模型的准确性为特征排序,借此来选择特征,另外,记得JMLR'03上有一篇论文介绍了一种基于决策树的特征选择方法,本质上是等价的。
当选择到了目标特征之后,再用来训练最终的模型;
3. 通过L1正则项来选择特征:L1正则方法具有稀疏解的特性,因此天然具备特征选择的特性,但是要注意,L1没有选到的特征不代表不重要,
原因是两个具有高相关性的特征可能只保留了一个,如果要确定哪个特征重要应再通过L2正则方法交叉检验;
4. 训练能够对特征打分的预选模型:RandomForest和Logistic Regression等都能对模型的特征打分,通过打分获得相关性后再训练最终模型;
5. 通过特征组合后再来选择特征:如对用户id和用户特征最组合来获得较大的特征集再来选择特征,这种做法在推荐系统和广告系统中比较常见,
这也是所谓亿级甚至十亿级特征的主要来源,原因是用户数据比较稀疏,组合特征能够同时兼顾全局模型和个性化模型,这个问题有机会可以展开讲。
6. 通过深度学习来进行特征选择:目前这种手段正在随着深度学习的流行而成为一种手段,尤其是在计算机视觉领域,原因是深度学习具有自动学习特征的能力,
这也是深度学习又叫unsupervised feature learning的原因。从深度学习模型中选择某一神经层的特征后就可以用来进行最终目标模型的训练了。
整体上来说,特征选择是一个既有学术价值又有工程价值的问题,目前在研究领域也比较热,值得所有做机器学习的朋友重视。
(2) 比较好的特征选择方法,除了卡方检验外还有就是信息增益(xgboost也可以实现) ---- 若是自己实现InfoGain,同时回带来一个问题:决策树如何对连续性特征进行分段?
决策树对于连续性特征(比如数字特征:比如符合一点分布的类似高斯分布)进行分段呢?举个例子,一组特征为0~5的连续数字,决策树如何分段生成类似:x<3,x>=3的if-else规则呢?,如何确定分段点是3而不是其他呢?
并不用考虑每一个example, 对第i个feature,首先以feature i 为key sort(feature_i, label_i)然后将label 有变动的地方作为可能的划分点,
比如 label 为[1,1,0,0,0,1]只需要考虑两个地方即 [1,1]后面 和[1,1,0,0,0]后面。对于每一个可能的划分点可以求information gain 让他最大,在求information gain 的时候可以用entropy 也可以用gini。
(3)实例代码 (没有解决连续特征问题)
1, pearson 相关系数(Pearson Correlation Coeffient) --- 皮尔逊相关系数
2,信息增益(InfoGain) 、卡方检验 与特征选择
3,机器学习模型中不平衡样本问题
1,pearson 相关系数(Pearson Correlation Coeffient) --- 皮尔逊相关系数:
(1)皮尔逊相关系数的适用范围:
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
1). 两个变量之间是线性关系,都是连续数据。
2). 两个变量的总体是正态分布,或接近正态的单峰分布。
3). 两个变量的观测值是成对的,每对观测值之间相互独立。
(2)定义:
第一种形式(也就是定义的形式):
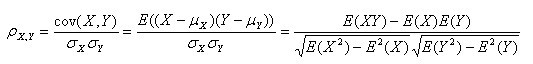
其变形(第二种形式):
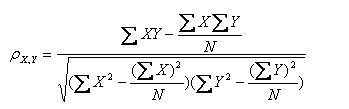
(其中,E为数学期望或均值,N为数据的数目,E{
[X-E(X)] [Y-E(Y)]}称为随机变量X与Y的协方差,记为Cov(X,Y))
(3)代码实现:
#encoding=utf8
from math import sqrt
import sys
import traceback
def multiply(a,b):
#a,b两个列表的数据一一对应相乘之后求和
sum_ab=0.0
for i in range(len(a)):
temp=a[i]*b[i]
sum_ab+=temp
return sum_ab
def cal_pearson(x,y):
n=len(x)
#求x_list、y_list元素之和
sum_x=sum(x)
sum_y=sum(y)
#求x_list、y_list元素乘积之和
sum_xy=multiply(x,y)
#求x_list、y_list的平方和
sum_x2 = sum([pow(i,2) for i in x])
sum_y2 = sum([pow(j,2) for j in y])
molecular=sum_xy-(float(sum_x)*float(sum_y)/n)
#计算Pearson相关系数,molecular为分子,denominator为分母
denominator=sqrt((sum_x2-float(sum_x**2)/n)*(sum_y2-float(sum_y**2)/n))
if denominator!=0:
return molecular/denominator
else:
return 0
data={}
data_y = {}
idx_2_pearson = {}
def load_data(file_in):
f=open(file_in,'r')
lable = 0
lines=f.readlines()
for line in lines:
#strip用于去掉换行符,split()通过指定分隔符对字符串进行切片,返回子字符串
cols=line.strip('\n').split(' ')
for i in range(len(cols)):
#float将字符串转成浮点数
if i == 0:
lable = float(cols[0])
continue
idx_val = cols[i].split(":")
if len(idx_val) < 2:
continue
try:
idx = int(idx_val[0])
val = float(idx_val[1])
data.setdefault(idx,[]).append(val)
data_y.setdefault(idx,[]).append(lable)
except:
traceback.print_exc()
def print_result():
#idx_pearson_list = sorted(idx_2_pearson.items(), key=lambda d: abs(d[1]), reverse=True)
idx_pearson_list = sorted(idx_2_pearson.items(), key=lambda d: abs(d[1]), reverse=True)
for idx, pearson_score in idx_pearson_list:
print idx, pearson_score
def cal_pearson_one_by_one():
for idx, Xi in data.items():
lables=data_y[idx]
#print lables,Xi
#print ("x_list,y_list的Pearson相关系数为:"+str(cal_pearson(lables,Xi)))
#print idx, cal_pearson(lables, Xi)
idx_2_pearson[idx] = cal_pearson(lables, Xi)
print_result()
if __name__=='__main__':
load_data(sys.argv[1])
cal_pearson_one_by_one()2,机器学习模型中不平衡样本问题
(1)为什么不平衡学习
传统的学习方法以降低总体分类精度为目标,将所有样本一视同仁,同等对待,造成了分类器在多数类的分类精度较高而在少数类的分类精度很低。
机器学习模型都有一个待优化的损失函数,以我们最常用最简单的二元分类器逻辑回归为例,逻辑回归以优化总体的精度为目标,
不同类别的误分类情况产生的误差是相同的,考虑一个$500:1$的数据集,即使把所有样本都预测为多数类其精度也能达到$500/501$之高,
很显然这并不是一个很好的学习效果,因此传统的学习算法在不平衡数据集中具有较大的局限性。
(2)解决方案:
解决方法主要分为两个方面,第一种方案主要从数据的角度出发,主要方法为抽样,可以通过某种策略进行抽样,让我们的数据相对均衡一些;
第二种方案从算法的角度出发,考虑不同误分类情况代价的差异性对算法进行优化。

另外可以参考 另外一篇文章
3,信息增益与特征选择
(1) 知乎上综述:
特征选择是特征工程中的重要问题(另一个重要的问题是特征提取),坊间常说:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
由此可见,特征工程尤其是特征选择在机器学习中占有相当重要的地位。
通常而言,特征选择是指选择获得相应模型和算法最好性能的特征集,工程上常用的方法有以下:
1. 计算每一个特征与响应变量的相关性:工程上常用的手段有计算皮尔逊系数和互信息系数,皮尔逊系数只能衡量线性相关性而互信息系数能够很好地度量各种相关性,
但是计算相对复杂一些,好在很多toolkit里边都包含了这个工具(如sklearn的MINE),得到相关性之后就可以排序选择特征了;
2. 构建单个特征的模型,通过模型的准确性为特征排序,借此来选择特征,另外,记得JMLR'03上有一篇论文介绍了一种基于决策树的特征选择方法,本质上是等价的。
当选择到了目标特征之后,再用来训练最终的模型;
3. 通过L1正则项来选择特征:L1正则方法具有稀疏解的特性,因此天然具备特征选择的特性,但是要注意,L1没有选到的特征不代表不重要,
原因是两个具有高相关性的特征可能只保留了一个,如果要确定哪个特征重要应再通过L2正则方法交叉检验;
4. 训练能够对特征打分的预选模型:RandomForest和Logistic Regression等都能对模型的特征打分,通过打分获得相关性后再训练最终模型;
5. 通过特征组合后再来选择特征:如对用户id和用户特征最组合来获得较大的特征集再来选择特征,这种做法在推荐系统和广告系统中比较常见,
这也是所谓亿级甚至十亿级特征的主要来源,原因是用户数据比较稀疏,组合特征能够同时兼顾全局模型和个性化模型,这个问题有机会可以展开讲。
6. 通过深度学习来进行特征选择:目前这种手段正在随着深度学习的流行而成为一种手段,尤其是在计算机视觉领域,原因是深度学习具有自动学习特征的能力,
这也是深度学习又叫unsupervised feature learning的原因。从深度学习模型中选择某一神经层的特征后就可以用来进行最终目标模型的训练了。
整体上来说,特征选择是一个既有学术价值又有工程价值的问题,目前在研究领域也比较热,值得所有做机器学习的朋友重视。
(2) 比较好的特征选择方法,除了卡方检验外还有就是信息增益(xgboost也可以实现) ---- 若是自己实现InfoGain,同时回带来一个问题:决策树如何对连续性特征进行分段?
决策树对于连续性特征(比如数字特征:比如符合一点分布的类似高斯分布)进行分段呢?举个例子,一组特征为0~5的连续数字,决策树如何分段生成类似:x<3,x>=3的if-else规则呢?,如何确定分段点是3而不是其他呢?
并不用考虑每一个example, 对第i个feature,首先以feature i 为key sort(feature_i, label_i)然后将label 有变动的地方作为可能的划分点,
比如 label 为[1,1,0,0,0,1]只需要考虑两个地方即 [1,1]后面 和[1,1,0,0,0]后面。对于每一个可能的划分点可以求information gain 让他最大,在求information gain 的时候可以用entropy 也可以用gini。
(3)实例代码 (没有解决连续特征问题)
#!/usr/bin/python
#encoding=gbk
import sys
import traceback
import math
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
## count by label
for featVec in dataSet:
currentLabel = featVec[0]
if currentLabel not in labelCounts:
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
## calculate entropy & information gain by probability(word frequency)
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries
shannonEnt -= (prob * math.log(prob, 2) )
return shannonEnt
# params 待划分的数据集, 划分数据集的特征, 划分数据的特征所对应的特征值
# return 按照axis (特征下标) & value(特征值) 返回的数据集
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value: ### 是不是可以改成>, < 等其他的符号呢
reduceFeatVec = featVec[:axis]
reduceFeatVec.extend(featVec[axis+1:])
retDataSet.append(reduceFeatVec)
else:
pass
return retDataSet
## this function (chooseBestFeatureToSplit) will call two funs (calcShannonEnt & splitDataSet)
## data require: 1,数据必须是一种由列表元素组成的列表(二维数组),并且数据维度相同;
## 2,数据的第一列(idx=0)是当前实例的标签; 3,数据类型没有要求,既可以是数字也可是是字符串
### 信息增益是熵的减少 或者 是数据无序度的减少
## return the bestFeature idx...
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) -1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
i = 0
while i < numFeatures:
i += 1 ## because the first val in list is lable
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals: ## 如果离散值太多,>>100, 就会带来问题
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
## OutPut
print i, infoGain
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i
return bestFeature
## deal with the anomaly...
import operator
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.itemitems(), key=operator.itemgetter(1), reverse=True)
## same to sorted(classCount.items(), key=lambda d: d[1], reverse=True)
return sortedClassCount[0][0]
## python 的传参是引用,所以每次递归调用时,都要重新建立数据集
def createTree(dataSet, labels):
classList = [example[0] for example in dataSet]
if classList.count(classList[0]) == len(classList): ## already same lable
return classList[0]
if len(dataSet[0]) == 1: ## 遍历完所有特征时,仍然无法将数据集划分成为仅包含唯一类别的组,则返回出现次数最多的label
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
print >> sys.stderr,"##", bestFeat, labels, dataSet
bestFeatLabel = labels[bestFeat] ## 根据bestFeat(idx)取得label
myTree = {bestFeatLabel: {} }
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) ## recursive fun..
return myTree
## decisionTree store and fetch
def storeTree(inputTree, filename):
import pickle
fw = open(filename, 'w')
pickle.dump(inputTree, fw) ## 序列化对象到磁盘上,用的时候再读取出来即可,不用每次都重新训练生成决策树
fw.close()
## load model..
def grabTree(filename):
import pickle
fr = open(filename, 'r')
return pickle.load(fr)
## use this decisionTree model to classify...
def classify(inputTree, featLabels, testVec):
firstStr = inputTree.keys()[0]
secondDict = inputTree[firstStr]
print >> sys.stderr, "&&", firstStr, secondDict
featIndex = featLabels.index(firstStr) ## 将标签字符串转化为索引
classLabel = None
for key in secondDict.keys():
if testVec[featIndex-1] == key: ### labels idx_0 is non_using, so need to -1
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel
## 1--1 Init data
def createDataSet():
dataSet = [['1', 1, 1],
['1', 1, 1],
['0', 1, 0],
['0', 0, 1],
['0', 0, 1]]
labels = ['label_ignore', 'sunshine', 'non-sunshine']
return dataSet, labels
## 1--2 Init data
def load_data(file_in):
labels = ['label_ignore', 'sunshine', 'non-sunshine']
dataSet = []
f=open(file_in,'r')
lable = 0
lines=f.readlines()
for line in lines:
#strip用于去掉换行符,split()通过指定分隔符对字符串进行切片,返回子字符串
data=[]
idx_cur = 0 ## is next
cols=line.strip('\n').split(' ')
for i in range(len(cols)):
#float将字符串转成浮点数
if i == 0:
data.append(float(cols[0]))
idx_cur += 1
continue
idx_val = cols[i].split(":")
if len(idx_val) < 2:
continue
try:
idx = int(idx_val[0])
val = float(idx_val[1])
## sparse ---> dense...
while idx_cur < idx:
data.append(0.0)
idx_cur += 1
data.append(val)
idx_cur += 1
except:
traceback.print_exc()
## sparse ---> dense...
while idx_cur < 1000:
data.append(0.0)
idx_cur += 1
dataSet.append(data)
#print data
return dataSet, labels
def test1():
myDat, labels = createDataSet()
## just two labels
print myDat
print calcShannonEnt(myDat)
print splitDataSet(myDat, 1, 1)
print splitDataSet(myDat, 1, 0)
def test2():
myDat, labels = createDataSet()
## change the first sample for a new lable, then the entropy will add
myDat[0][0] = '2'
print myDat
print calcShannonEnt(myDat)
def test3():
myDat, labels = load_data(sys.argv[1])
## change the first sample for a new lable, then the entropy will add
#print myDat
print chooseBestFeatureToSplit(myDat)
def test4():
myDat, labels = createDataSet()
print myDat, labels
storeTree(labels, "labels.txt")
decisionTree = createTree(myDat, labels)
print decisionTree
storeTree(decisionTree, "decisionTree.txt")
def test5():
decisionTree = grabTree("decisionTree.txt")
labels = grabTree("labels.txt")
print "###", decisionTree, labels
#testSample = [2, 0]
testSample = [1, 0]
#testSample = [1, 1]
preLabel = classify(decisionTree, labels, testSample)
print "predict label: ", preLabel
if "__main__" == __name__:
#test1()
#test2()
test3()
#test4()
#test5()
相关文章推荐
- 机器学习模型构建时正负样本不平衡带来的问题及解决方法
- 类间样本数量不平衡对分类模型性能的影响问题
- 机器学习中的数据不平衡问题----通过随机采样比例大的类别使得训练集中大类的个数与小类相当,或者模型中加入惩罚项
- 类间样本数量不平衡对分类模型性能的影响问题
- python机器学习模型选择&调参工具Hyperopt-sklearn(1)——综述&分类问题
- 机器学习笔记(X)线性模型(VI)类别不平衡问题
- Pearson(皮尔逊)相关系数
- C# AutoCAD 二次开发相关问题 "被呼叫方拒绝接收呼叫"
- baidu 留言板& 相关问题解决
- 利用"线段树"相关算法解决有关数组的问题[待续]
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
- Windows编码相关知识 & VC与MySQL交互数据乱码问题
- "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd" 的相关问题
- resin3.0&amp;3.1配置相关问题解决办法
- SAP3.0相关问题,Could not load file or assembly 'sapnco, Version=3.0.0.42
- 相关性分析 -pearson spearman kendall相关系数
- 求高手指点"魔方数的输出'的相关问题
- 细品javascript 寻址,闭包,对象模型和相关问题
- [IIS问题类]Service Unavailable错误,'DefaultAppPool' 相关,(应用程序池 'DefaultAppPool' 被自动禁用,原因是为此应用程序池提供服务的进程中出现一系列错误)
- 细品JS的寻址,闭包,对象模型和相关问题
