2017计蒜之道程序设计大赛复赛题解
2017-06-10 22:02
351 查看
比赛链接
题目可以在比赛的题目列表中查看
令 f_p(n)fp(n) 表示满足 1
\leq x < n1≤x<n 且 xx 是合法秘钥的正整数 xx 的数量,所求即 f_p(R
+ 1) - f_p(L)fp(R+1)−fp(L)。
f_p(n)fp(n) 的计算也很简单,如果正整数 xx 满足 1
\leq x < n1≤x<n ,那么 xx 的 pp 进制表示必然有一位取值小于 nn 的 pp 进制表示里对应位取值,将 xx 按照最高的"小于位"进行划分,则 xx 的高于"小于位"的部分与 nn 相同,可直接判断是否破坏秘钥性质,而低于"小于位"的部分则可以取到任意值,这一部分可以考虑预处理出来。
预处理 pp 进制表示长度为 ii 且最高位是 jj 的秘钥有多少种,枚举"小于位"的位置,枚举"小于位"的具体值(如果存在更高位,需要与相邻的高位互质),利用预处理的信息统计答案即可。
预处理的信息需要使用莫比乌斯反演加速求解,令 g_p(i,
j)gp(i,j) 表示 pp 进制表示长度为 ii 且最高位是 jj的秘钥的数量,则当 i
> 0i>0 时有:
\begin{array}{lcl}g_p(i,
j) &=& \sum_{1 \leq k < p} {[\gcd(j, k) = 1] g_p(i - 1, k)} \\&=& \sum_{d \mid j}{\mu(d)\sum_{1 \leq k < p, d \mid k}{g_p(i - 1, k)}} \\&=& \sum_{d \mid j}{\mu(d) h_p(i - 1, d)}\end{array}gp(i,j)===∑1≤k<p[gcd(j,k)=1]gp(i−1,k)∑d∣jμ(d)∑1≤k<p,d∣kgp(i−1,k)∑d∣jμ(d)hp(i−1,d)
其中 h_p(i,
j) = \sum_{1 \leq k < p, j \mid k}{g_p(i, k)}hp(i,j)=∑1≤k<p,j∣kgp(i,k)。
时间复杂度为 \mathcal{O}(p
\log_{2}{p} \log_{p}{R}) = \mathcal{O}(p \log_{2}{R})O(plog2plogpR)=O(plog2R)。
在 Windows 的“画图”工具里,可以绘制各种各样的图案。可以把画图当做一个标准的二维平面,在其上先后绘制了 nn 条颜色互不相同的线段。
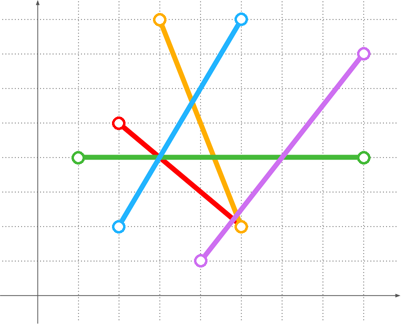
按绘制的时间顺序,从先到后把线段依次编号为 11 到 nn。第 ii 条线段的两个端点分别为 (xa_i,ya_i)(xai,yai) 和 (xb_i,yb_i)(xbi,ybi),线段的粗细忽略不计。后绘制的线段不会改变之前绘制的线段的位置。
请写一个程序,回答 qq 组询问,每组询问给出一个坐标 (x_i,y_i)(xi,yi),你需要算出在这个点上最后绘制的线段编号。
第一行包含两个正整数 n,m(1\leq
n\leq 80000,1\leq m\leq 250)n,m(1≤n≤80000,1≤m≤250),分别表示线段的数目以及坐标的最大取值(下面会具体说明)。
接下来 nn 行,每行输入四个正整数 xa_i,ya_i,xb_i,yb_ixai,yai,xbi,ybi (1\leq
xa_i,ya_i,xb_i,yb_i\leq m,(1≤xai,yai,xbi,ybi≤m, (xa_i,ya_i)\neq(xb_i,yb_i))(xai,yai)≠(xbi,ybi)),依次表示每条线段两个端点的坐标。
接下来一行,输入一个正整数 q(1\leq
q\leq 62500)q(1≤q≤62500),表示询问的组数。
接下来 qq 行,每行输入两个正整数 x_i,y_i(1\leq
x_i,y_i\leq m)xi,yi(1≤xi,yi≤m),分别表示每组询问的坐标。
输出 qq 行,每行一个整数,表示该位置最上面(最后绘制)的线段的编号。
若该点上不存在线段,请输出 00。
样例对应题目描述中的图。
题目大意:中文题
解题思路:模拟一下,紫书上有线段上整点分析,用gcd
注意到线段上点数为 O(m)O(m),故对于每个线段,暴力枚举所有位于线段上的整点即可。
首先特判掉水平和竖直的线段,然后对于坐标差分别为 dxdx 和 dydy 的线段,令 d=\gcd(dx,dy)d=gcd(dx,dy),那么 xx 每隔 \frac{dx}{d}ddx 个,yy 每隔 \frac{dy}{d}ddy 个就是整点,由此方法可以很方便地枚举所有整点。
AC代码1:
AC代码2:
AC代码3:
限制是加在相互连通的点之间的,因此只需要考虑如何使每个连通块满足限制。如果连通块中点数不超过 33 ,那么显然是满足条件的,否则总能找到一条点数至少为 44 的简单路径。不妨设其依次经过的点是 p_0,
p_1, \cdots, p_{k - 1}p0,p1,⋯,pk−1 (共 kk 个点)。由于限制条件的原因,p_ipi 和 p_{i
+ 3}pi+3 总是相连的 (i
= 0, 1, \cdots, k - 4)(i=0,1,⋯,k−4) ,从而对于任意一条简单路径,可以推导出一个完全二分图。但是当连通块中存在奇数长度的环时,将环拆成两条路径则可以推导出完全图。
因此我们可以得到一个结论,对于点数为 nn 的连通块,若 n
\neq 2n≠2 ,满足限制的不同构图有 \left
\lfloor \frac{n}{2} \right \rfloor + 1⌊2n⌋+1 种,否则有 11 种。这是因为点数相同但却不同构的完全二分图可以通过两边点数的最小值来区分,而 n
= 2n=2 时完全图就是完全二分图,n
> 2n>2 时完全图一定存在奇数长度的环,从而与完全二分图区分开来。
现在是考虑如何将不同的连通块组合在一起,凑成恰好 nn 个点的无向图,注意到点数为 ii 的连通块只有 \mathcal{O}(i)O(i) 种,把它们视为不同的体积为 ii 的物品,则有 \mathcal{O}(n^2)O(n2) 种物品,直接进行背包型动态规划的时间复杂度是 \mathcal{O}(n^3)O(n3),难以接受。
事实上,体积相同的不同物品在进行状态转移时可以合并在一起处理,具体来说就是枚举体积为 ii的物品选多少个,从多种物品里面直接选即可(等价于可重集排列的数量),这样做的时间复杂度是 \mathcal{O}(\sum_{i
= 1}^{n}{n \frac{n}{i}}) = \mathcal{O}(n^2 \log n)O(∑i=1nnin)=O(n2logn)。
沿用上文中的定义与结论,再设体积为 ii 的物品有 a(i)a(i) 种,所求恰好有 nn 个点的图有 f(n)f(n) 种,这里 f(0)
= 1f(0)=1 ,对应生成函数为 F(x)
= \sum_{n \geq 0}{f(n) x^n}F(x)=∑n≥0f(n)xn ,那么有
F(x)
= \prod_{1 \leq i \leq n}{\frac{1}{(1-x^i)^{a(i)}}},F(x)=∏1≤i≤n(1−xi)a(i)1,
等式两边常数项均为 11 ,取自然对数得
\ln
F(x) = -\sum_{1 \leq i \leq n}{a(i) \ln(1 - x^i)} = \sum_{1 \leq i \leq n}{a(i) \sum_{j \geq 1}{\frac{x^{ij}}{j}}},lnF(x)=−∑1≤i≤na(i)ln(1−xi)=∑1≤i≤na(i)∑j≥1jxij,
此外有
\ln
F(x) = \int{\frac{\mathrm{d}F}{F}} = \int{\frac{\mathrm{d}F}{\mathrm{d}x}\frac{\mathrm{d}x}{F}} = \int{\frac{F'(x)}{F(x)}\mathrm{d}x},lnF(x)=∫FdF=∫dxdFFdx=∫F(x)F′(x)dx,
结合到之前的式子中,由于等式两边常数项均为 00,求导后整理可得,当 n
> 0n>0 时
n
f(n) = \sum_{i = 1}^{n}{f(n - i) \sum_{d \mid i}{d \ a(d)}},nf(n)=∑i=1nf(n−i)∑d∣id a(d),
故预处理 b(n)
= \sum_{d \mid n}{d \ a(d)}b(n)=∑d∣nd a(d) 后直接求解即可,时间复杂度 \mathcal{O}(n^2)O(n2) 。
沿用上文中的定义与结论,我们可以发现
n
f(n) = \sum_{i = 1}^{n}{f(n - i) b(i)}nf(n)=∑i=1nf(n−i)b(i)
是一个很明显的卷积式子,但是 ff 同时出现在等式两边。
幸好出现在等式右边的 ff 下标是完全小于 nn 的,故可以采用分治的做法,将低位对高位的贡献产生,采用快速傅里叶变换加速这个过程,做到时间复杂度 \mathcal{O}(n
\log^2 n)O(nlog2n) 。如果对多项式求幂指数有了解,可以做到时间复杂度 \mathcal{O}(n
\log n)O(nlogn) ,但常数较大。
在采用快速傅里叶变换加速卷积过程的同时,需要注意到 pp 可以达到 (2^{30}
- 35)(230−35) ,这意味着使用浮点数直接卷积不一定能保证精度,而使用数论变换结合中国剩余定理可能会超时。一种可行的做法是将系数表示成 \left
\lceil \sqrt{p} \right \rceil⌈√p⌉ 进制,多项式可以写成两个系数小于进制数的多项式的线性组合,将两个多项式的卷积改成四个"小多项式"的卷积,利用实数序列可以合并起来进行离散傅里叶变换的技巧,做到两次
DFT 和两次 IDFT 完成两个多项式的卷积。
百度地图上有 nn 个城市,城市编号依次为 11 到 nn。地图中有若干个城市群,编号依次为 11 到 mm。每个城市群包含一个或多个城市;每个城市可能属于多个城市群,也可能不属于任何城市群。
地图中有两类道路。第一类道路是 城市之间的快速路,两个城市 u,vu,v 之间增加一条距离为 cc 的边;第二类道路是 城市群之间的高速路,连接两个城市群 a,ba,b,通过这条高速路,城市群 aa 里的每个城市与城市群 bb 里的每个城市之间两两增加一条距离为 cc 的边。图中所有边均为无向边。
你需要计算从城市 ss 到城市 tt 的最短路。
第一行输入 n(1≤n≤20000),n(1≤n≤20000), m(0≤m≤20000)m(0≤m≤20000),分别表示城市总数和城市群总数。
接下来一共输入 mm 行。
第 ii 行首先输入一个 ki(1≤ki≤n)ki(1≤ki≤n),表示第 ii 个城市群中的城市数为 kiki。接下来输入 kiki 个数,表示第 ii 个城市群中每个城市的编号(保证一个城市群内的城市编号不重复且合法,∑i=1mki≤20000∑i=1mki≤20000)。
下一行输入一个整数 m1(0≤m1≤20000)m1(0≤m1≤20000),表示有 m1m1 条第一类道路,即 城市之间的快速路。
接下来 m1m1 行,每行输入三个整数 ui,vi(1≤ui,vi≤n),ci(1≤ci≤106)ui,vi(1≤ui,vi≤n),ci(1≤ci≤106),分别表示快速路连接的两个城市编号和边的距离。
下一行输入一个整数 m2(0≤m2≤20000)m2(0≤m2≤20000),表示有 m2m2 条第二类道路,即 城市群之间的高速路。
接下来 m2m2 行,每行输入三个整数 ai,bi(1≤ai,bi≤m),li(1≤li≤106)ai,bi(1≤ai,bi≤m),li(1≤li≤106),分别表示快速路连接的两个城市群编号和边的距离。
最后一行输入 s,t(1≤s,t≤n)s,t(1≤s,t≤n),表示起点和终点城市编号。
输出一个整数,表示城市 ss 到城市 tt 到最短路。如果不存在路径,则输出
把每个城市群抽象成两个点 s',
s''s′,s′′。按照如下方式见图:
对于每个城市群里面的城市 s_isi,连边:(s_i,
s', 0)(si,s′,0), (s'',
s_i, 0)(s′′,si,0);
第一种边正常连边:(u,
v, c), (v, u, c)(u,v,c),(v,u,c);
第二种边连边:(a',
b'', l)(a′,b′′,l), (b',
a'', l)(b′,a′′,l)。
然后跑一遍 s-ts−t 最短路就是答案。
AC代码1:
把每个城市群也看成点,注意分成入点和出点。
首先,可以判断,当 xx 与 yy 的和或差是奇数、或者 xx 小于 yy 时,答案为 00。
对于其它情况,如果我们枚举走 \left
( a + 2,b \right )(a+2,b) 的步数,由组合数的知识,我们可以得出
ans=\sum_{i=0}^{min\left
( \frac{x+y}{2} , \frac{x - y}{2} \right )}\frac{\left ( x - i \right )!}{i!\left ( \frac{x+y}{2} - i \right )!\left ( \frac{x - y}{2} - i \right )!}ans=∑i=0min(2x+y,2x−y)i!(2x+y−i)!(2x−y−i)!(x−i)!
不妨令 n
= \frac{x+y}{2},n=2x+y, m
= \frac{x - y}{2}m=2x−y,且 n
\leq mn≤m。那么有
ans=\sum_{i=0}^{n}\frac{\left
( x - i \right )!}{i!\left ( n - i \right )!\left ( m - i \right )!} = \sum_{i=0}^{n}C_{x-i}^{i}C_{x-2i}^{n-i}ans=∑i=0ni!(n−i)!(m−i)!(x−i)!=∑i=0nCx−iiCx−2in−i
因为模数 pp 比较小,所以我们考虑对上述和式的每一项使用
Lucas 定理,那么第 ii 项就可以写成
C_{\left
( x-i \right )/p}^{i/p}C_{\left ( x-2i \right )/p}^{\left ( n-i \right )/p}C_{\left ( x-i \right )\%p}^{i\%p}C_{\left ( x-2i \right )\%p}^{\left ( n-i \right )\%p}=C_{\left ( x-i \right )/p}^{i/p} C_{\left ( x-i \right )/p-i/p}^{\left ( n-i \right )/p} C_{\left
( x-i \right )\%p}^{i\%p}C_{\left ( x-i \right )\%p-i\%p}^{\left ( n-i \right )\%p}C(x−i)/pi/pC(x−2i)/p(n−i)/pC(x−i)%pi%pC(x−2i)%p(n−i)%p=C(x−i)/pi/pC(x−i)/p−i/p(n−i)/pC(x−i)%pi%pC(x−i)%p−i%p(n−i)%p
可以证明,右式和左式是等价的。
然后,我们可以发现,对于第 ii 项和第 i+pi+p 项:
C_{\left
( x-i \right )\%p}^{i\%p}C_{\left ( x-i \right )\%p-i\%p}^{\left ( n-i \right )\%p}=C_{\left ( x-i-p \right )\%p}^{\left ( i+p \right )\%p}C_{\left ( x-i-p \right )\%p-\left ( i+p \right )\%p}^{\left ( n-i-p \right )\%p}C(x−i)%pi%pC(x−i)%p−i%p(n−i)%p=C(x−i−p)%p(i+p)%pC(x−i−p)%p−(i+p)%p(n−i−p)%p
那么,我们就可以将第 i,i+p,i+2p,i+3p\cdotsi,i+p,i+2p,i+3p⋯ 项进行合并,而对于它们不相同的部分,我们可以重复上述步骤进行合并。
最后,我们成功地将答案化为了 log_{p}xlogpx 个项数小于等于 pp 的和式的乘积,每一个和式都可以通过预处理在 O\left
( p \right )O(p) 的时间内计算出。
总体复杂度:O\left
( plog_{p}x \right )O(plogpx)。
用 f(mask,step)f(mask,step) 表示考虑当前 maskmask 集合内的数用 stepstep 步删除完的方案数,每次转移则可以简单地用 O(n^2)O(n2) 来进行枚举删掉的一段区间进行转移。
直接暴力状压,O(2nn3)可以过。
题目可以在比赛的题目列表中查看
A题:阿里云秘钥池
令 f_p(n)fp(n) 表示满足 1\leq x < n1≤x<n 且 xx 是合法秘钥的正整数 xx 的数量,所求即 f_p(R
+ 1) - f_p(L)fp(R+1)−fp(L)。
f_p(n)fp(n) 的计算也很简单,如果正整数 xx 满足 1
\leq x < n1≤x<n ,那么 xx 的 pp 进制表示必然有一位取值小于 nn 的 pp 进制表示里对应位取值,将 xx 按照最高的"小于位"进行划分,则 xx 的高于"小于位"的部分与 nn 相同,可直接判断是否破坏秘钥性质,而低于"小于位"的部分则可以取到任意值,这一部分可以考虑预处理出来。
预处理 pp 进制表示长度为 ii 且最高位是 jj 的秘钥有多少种,枚举"小于位"的位置,枚举"小于位"的具体值(如果存在更高位,需要与相邻的高位互质),利用预处理的信息统计答案即可。
预处理的信息需要使用莫比乌斯反演加速求解,令 g_p(i,
j)gp(i,j) 表示 pp 进制表示长度为 ii 且最高位是 jj的秘钥的数量,则当 i
> 0i>0 时有:
\begin{array}{lcl}g_p(i,
j) &=& \sum_{1 \leq k < p} {[\gcd(j, k) = 1] g_p(i - 1, k)} \\&=& \sum_{d \mid j}{\mu(d)\sum_{1 \leq k < p, d \mid k}{g_p(i - 1, k)}} \\&=& \sum_{d \mid j}{\mu(d) h_p(i - 1, d)}\end{array}gp(i,j)===∑1≤k<p[gcd(j,k)=1]gp(i−1,k)∑d∣jμ(d)∑1≤k<p,d∣kgp(i−1,k)∑d∣jμ(d)hp(i−1,d)
其中 h_p(i,
j) = \sum_{1 \leq k < p, j \mid k}{g_p(i, k)}hp(i,j)=∑1≤k<p,j∣kgp(i,k)。
时间复杂度为 \mathcal{O}(p
\log_{2}{p} \log_{p}{R}) = \mathcal{O}(p \log_{2}{R})O(plog2plogpR)=O(plog2R)。
B题:Windows 画图
在 Windows 的“画图”工具里,可以绘制各种各样的图案。可以把画图当做一个标准的二维平面,在其上先后绘制了 nn 条颜色互不相同的线段。
按绘制的时间顺序,从先到后把线段依次编号为 11 到 nn。第 ii 条线段的两个端点分别为 (xa_i,ya_i)(xai,yai) 和 (xb_i,yb_i)(xbi,ybi),线段的粗细忽略不计。后绘制的线段不会改变之前绘制的线段的位置。
请写一个程序,回答 qq 组询问,每组询问给出一个坐标 (x_i,y_i)(xi,yi),你需要算出在这个点上最后绘制的线段编号。
输入格式
第一行包含两个正整数 n,m(1\leqn\leq 80000,1\leq m\leq 250)n,m(1≤n≤80000,1≤m≤250),分别表示线段的数目以及坐标的最大取值(下面会具体说明)。
接下来 nn 行,每行输入四个正整数 xa_i,ya_i,xb_i,yb_ixai,yai,xbi,ybi (1\leq
xa_i,ya_i,xb_i,yb_i\leq m,(1≤xai,yai,xbi,ybi≤m, (xa_i,ya_i)\neq(xb_i,yb_i))(xai,yai)≠(xbi,ybi)),依次表示每条线段两个端点的坐标。
接下来一行,输入一个正整数 q(1\leq
q\leq 62500)q(1≤q≤62500),表示询问的组数。
接下来 qq 行,每行输入两个正整数 x_i,y_i(1\leq
x_i,y_i\leq m)xi,yi(1≤xi,yi≤m),分别表示每组询问的坐标。
输出格式
输出 qq 行,每行一个整数,表示该位置最上面(最后绘制)的线段的编号。若该点上不存在线段,请输出 00。
样例解释
样例对应题目描述中的图。
样例输入
5 8 2 5 5 2 5 2 3 8 8 4 1 4 2 2 5 8 8 7 4 1 4 3 4 5 2 6 4 3 5
样例输出
4 2 5 0
题目大意:中文题
解题思路:模拟一下,紫书上有线段上整点分析,用gcd
注意到线段上点数为 O(m)O(m),故对于每个线段,暴力枚举所有位于线段上的整点即可。
首先特判掉水平和竖直的线段,然后对于坐标差分别为 dxdx 和 dydy 的线段,令 d=\gcd(dx,dy)d=gcd(dx,dy),那么 xx 每隔 \frac{dx}{d}ddx 个,yy 每隔 \frac{dy}{d}ddy 个就是整点,由此方法可以很方便地枚举所有整点。
AC代码1:
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<map>
#include<string>
using namespace std;
typedef long long LL;
const int MOD=100003;
int n,m,q;
int G[260][260];
int gcd(int a,int b)
{
return b==0?a:gcd(b,a%b);
}
struct seg
{
int sx,sy,tx,ty;
int id;
}s[80005];
void solve(int i)
{
double ty;
if(s[i].sx==s[i].tx)
{
if(s[i].sy<s[i].ty)
{
for(int j=s[i].sy;j<=s[i].ty;j++)
G[s[i].sx][j]=s[i].id;
}else
{
for(int j=s[i].ty;j<=s[i].sy;j++)
G[s[i].sx][j]=s[i].id;
}
}else if(s[i].sx<s[i].tx)
{
double a=(double)(s[i].ty-s[i].sy)/(s[i].tx-s[i].sx);
double c=-a*s[i].sx+s[i].sy;
int f1=s[i].ty-s[i].sy;
int f2=s[i].tx-s[i].sx;
for(int j=s[i].sx+1;j<=s[i].tx;j++)
{
ty=a*j+c;
if(gcd(f1*(j-s[i].sx),f2)==f2)
G[j][f1*(j-s[i].sx)/(f2)+s[i].sy]=s[i].id;
//if((int)ty==ty)
}
}else
{
double a=(double)(s[i].sy-s[i].ty)/(s[i].sx-s[i].tx);
double c=-a*s[i].tx+s[i].ty;
int f1=s[i].sy-s[i].ty;
int f2=s[i].sx-s[i].tx;
for(int j=s[i].tx+1;j<=s[i].sx;j++)
{
ty=a*j+c;
if(gcd(f1*(j-s[i].tx),f2)==f2)
G[j][f1*(j-s[i].tx)/f2+s[i].ty]=s[i].id;
//if((int)ty==ty)
}
}
}
int main()
{
while(cin>>n>>m)
{
memset(G,0,sizeof(G));
int sx,sy,tx,ty;
for(int i=1;i<=n;i++)
{
cin>>sx>>sy>>tx>>ty;
s[i].sx=sx;
s[i].sy=sy;
s[i].tx=tx;
s[i].ty=ty;
s[i].id=i;
G[sx][sy]=i;
G[tx][ty]=i;
solve(i);
}
cin>>q;
int x,y;
for(int i=1;i<=q;i++)
{
cin>>x>>y;
cout<<G[x][y]<<endl;
}
}
return 0;
}AC代码2:
#include<cstdio>
#include<algorithm>
using namespace std;
int ans[300][300],n,m,q;
int gcd(int x,int y)
{
return y?gcd(y,x%y):x;
}
int main()
{
int x,y,x1,y1,x2,y2,d,dx,dy;
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
d=gcd(abs(x1-x2),abs(y1-y2));
dx=(x1-x2)/d;
dy=(y1-y2)/d;
for (;;x2+=dx,y2+=dy)
{
ans[x2][y2]=i;
if (x2==x1) break;
}
}
scanf("%d",&q);
while (q--)
{
scanf("%d%d",&x,&y);
printf("%d\n",ans[x][y]);
}
}AC代码3:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int color[305][305];
int gcd(int a,int b)
{
return a%b?gcd(b,a%b):b;
}
int main()
{
int n,m;
int i;
int x1,y1,x2,y2;
int x,y;
int fx,fy;
int tim;
int T;
int t;
int g;
while(scanf("%d%d",&n,&m)!=EOF)
{
memset(color,0,sizeof(color));
for(i=1;i<=n;i++)
{
fx=-1;
fy=-1;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
color[x1][y1]=i;
color[x2][y2]=i;
if(x1<x2)
fx=1;
if(y1<y2)
fy=1;
x=abs(x1-x2);
y=abs(y1-y2);
if(x==0)
{
y--;
while(y--)
{
y1+=fy;
color[x1][y1]=i;
//cout<<"1color["<<x1<<"]["<<y1<<"] = "<<i<<endl;
}
continue;
}
if(y==0)
{
x--;
while(x--)
{
x1+=fx;
color[x1][y1]=i;
//cout<<"2color["<<x1<<"]["<<y1<<"] = "<<i<<endl;
}
continue;
}
g=gcd(x,y);
if(x%y==0||y%x==0)
{
if(x<y)
{
t=x;
x/=t;
y=y/t;
}
else if(x>y)
{
t=y;
y/=t;
x=x/t;
}
else
{
t=x;
y/=t;
x/=t;
}
while(x1!=x2)
{
x1+=fx*x;
y1+=fy*y;
color[x1][y1]=i;
//cout<<"3color["<<x1<<"]["<<y1<<"] = "<<i<<endl;
}
}
else if(g!=x&&g!=y)
{
if(x<y)
{
x/=g;
y=y/g;
}
else if(x>y)
{
y/=g;
x=x/g;
}
else
{
y/=g;
x/=g;
}
while(x1!=x2)
{
x1+=fx*x;
y1+=fy*y;
color[x1][y1]=i;
//cout<<"4color["<<x1<<"]["<<y1<<"] = "<<i<<endl;
}
}
//cout<<i<<" color is over"<<endl;
}
scanf("%d",&T);
for(i=0;i<T;i++)
{
scanf("%d%d",&x,&y);
cout<<color[x][y]<<endl;
}
}
return 0;
}
C题:UCloud 路由器网络
限制是加在相互连通的点之间的,因此只需要考虑如何使每个连通块满足限制。如果连通块中点数不超过 33 ,那么显然是满足条件的,否则总能找到一条点数至少为 44 的简单路径。不妨设其依次经过的点是 p_0,p_1, \cdots, p_{k - 1}p0,p1,⋯,pk−1 (共 kk 个点)。由于限制条件的原因,p_ipi 和 p_{i
+ 3}pi+3 总是相连的 (i
= 0, 1, \cdots, k - 4)(i=0,1,⋯,k−4) ,从而对于任意一条简单路径,可以推导出一个完全二分图。但是当连通块中存在奇数长度的环时,将环拆成两条路径则可以推导出完全图。
因此我们可以得到一个结论,对于点数为 nn 的连通块,若 n
\neq 2n≠2 ,满足限制的不同构图有 \left
\lfloor \frac{n}{2} \right \rfloor + 1⌊2n⌋+1 种,否则有 11 种。这是因为点数相同但却不同构的完全二分图可以通过两边点数的最小值来区分,而 n
= 2n=2 时完全图就是完全二分图,n
> 2n>2 时完全图一定存在奇数长度的环,从而与完全二分图区分开来。
现在是考虑如何将不同的连通块组合在一起,凑成恰好 nn 个点的无向图,注意到点数为 ii 的连通块只有 \mathcal{O}(i)O(i) 种,把它们视为不同的体积为 ii 的物品,则有 \mathcal{O}(n^2)O(n2) 种物品,直接进行背包型动态规划的时间复杂度是 \mathcal{O}(n^3)O(n3),难以接受。
事实上,体积相同的不同物品在进行状态转移时可以合并在一起处理,具体来说就是枚举体积为 ii的物品选多少个,从多种物品里面直接选即可(等价于可重集排列的数量),这样做的时间复杂度是 \mathcal{O}(\sum_{i
= 1}^{n}{n \frac{n}{i}}) = \mathcal{O}(n^2 \log n)O(∑i=1nnin)=O(n2logn)。
沿用上文中的定义与结论,再设体积为 ii 的物品有 a(i)a(i) 种,所求恰好有 nn 个点的图有 f(n)f(n) 种,这里 f(0)
= 1f(0)=1 ,对应生成函数为 F(x)
= \sum_{n \geq 0}{f(n) x^n}F(x)=∑n≥0f(n)xn ,那么有
F(x)
= \prod_{1 \leq i \leq n}{\frac{1}{(1-x^i)^{a(i)}}},F(x)=∏1≤i≤n(1−xi)a(i)1,
等式两边常数项均为 11 ,取自然对数得
\ln
F(x) = -\sum_{1 \leq i \leq n}{a(i) \ln(1 - x^i)} = \sum_{1 \leq i \leq n}{a(i) \sum_{j \geq 1}{\frac{x^{ij}}{j}}},lnF(x)=−∑1≤i≤na(i)ln(1−xi)=∑1≤i≤na(i)∑j≥1jxij,
此外有
\ln
F(x) = \int{\frac{\mathrm{d}F}{F}} = \int{\frac{\mathrm{d}F}{\mathrm{d}x}\frac{\mathrm{d}x}{F}} = \int{\frac{F'(x)}{F(x)}\mathrm{d}x},lnF(x)=∫FdF=∫dxdFFdx=∫F(x)F′(x)dx,
结合到之前的式子中,由于等式两边常数项均为 00,求导后整理可得,当 n
> 0n>0 时
n
f(n) = \sum_{i = 1}^{n}{f(n - i) \sum_{d \mid i}{d \ a(d)}},nf(n)=∑i=1nf(n−i)∑d∣id a(d),
故预处理 b(n)
= \sum_{d \mid n}{d \ a(d)}b(n)=∑d∣nd a(d) 后直接求解即可,时间复杂度 \mathcal{O}(n^2)O(n2) 。
沿用上文中的定义与结论,我们可以发现
n
f(n) = \sum_{i = 1}^{n}{f(n - i) b(i)}nf(n)=∑i=1nf(n−i)b(i)
是一个很明显的卷积式子,但是 ff 同时出现在等式两边。
幸好出现在等式右边的 ff 下标是完全小于 nn 的,故可以采用分治的做法,将低位对高位的贡献产生,采用快速傅里叶变换加速这个过程,做到时间复杂度 \mathcal{O}(n
\log^2 n)O(nlog2n) 。如果对多项式求幂指数有了解,可以做到时间复杂度 \mathcal{O}(n
\log n)O(nlogn) ,但常数较大。
在采用快速傅里叶变换加速卷积过程的同时,需要注意到 pp 可以达到 (2^{30}
- 35)(230−35) ,这意味着使用浮点数直接卷积不一定能保证精度,而使用数论变换结合中国剩余定理可能会超时。一种可行的做法是将系数表示成 \left
\lceil \sqrt{p} \right \rceil⌈√p⌉ 进制,多项式可以写成两个系数小于进制数的多项式的线性组合,将两个多项式的卷积改成四个"小多项式"的卷积,利用实数序列可以合并起来进行离散傅里叶变换的技巧,做到两次
DFT 和两次 IDFT 完成两个多项式的卷积。
D题:百度地图导航
百度地图上有 nn 个城市,城市编号依次为 11 到 nn。地图中有若干个城市群,编号依次为 11 到 mm。每个城市群包含一个或多个城市;每个城市可能属于多个城市群,也可能不属于任何城市群。地图中有两类道路。第一类道路是 城市之间的快速路,两个城市 u,vu,v 之间增加一条距离为 cc 的边;第二类道路是 城市群之间的高速路,连接两个城市群 a,ba,b,通过这条高速路,城市群 aa 里的每个城市与城市群 bb 里的每个城市之间两两增加一条距离为 cc 的边。图中所有边均为无向边。
你需要计算从城市 ss 到城市 tt 的最短路。
输入格式
第一行输入 n(1≤n≤20000),n(1≤n≤20000), m(0≤m≤20000)m(0≤m≤20000),分别表示城市总数和城市群总数。接下来一共输入 mm 行。
第 ii 行首先输入一个 ki(1≤ki≤n)ki(1≤ki≤n),表示第 ii 个城市群中的城市数为 kiki。接下来输入 kiki 个数,表示第 ii 个城市群中每个城市的编号(保证一个城市群内的城市编号不重复且合法,∑i=1mki≤20000∑i=1mki≤20000)。
下一行输入一个整数 m1(0≤m1≤20000)m1(0≤m1≤20000),表示有 m1m1 条第一类道路,即 城市之间的快速路。
接下来 m1m1 行,每行输入三个整数 ui,vi(1≤ui,vi≤n),ci(1≤ci≤106)ui,vi(1≤ui,vi≤n),ci(1≤ci≤106),分别表示快速路连接的两个城市编号和边的距离。
下一行输入一个整数 m2(0≤m2≤20000)m2(0≤m2≤20000),表示有 m2m2 条第二类道路,即 城市群之间的高速路。
接下来 m2m2 行,每行输入三个整数 ai,bi(1≤ai,bi≤m),li(1≤li≤106)ai,bi(1≤ai,bi≤m),li(1≤li≤106),分别表示快速路连接的两个城市群编号和边的距离。
最后一行输入 s,t(1≤s,t≤n)s,t(1≤s,t≤n),表示起点和终点城市编号。
输出格式
输出一个整数,表示城市 ss 到城市 tt 到最短路。如果不存在路径,则输出-1。
样例说明
1 -> 2 - > 5或者
1 -> 4 -> 5是最短的路径,总长度为 1212。
样例输入
5 4 2 5 1 2 2 4 1 3 2 3 4 2 1 2 9 1 5 18 2 1 2 6 1 3 10 1 5
样例输出
12
把每个城市群抽象成两个点 s',
s''s′,s′′。按照如下方式见图:
对于每个城市群里面的城市 s_isi,连边:(s_i,
s', 0)(si,s′,0), (s'',
s_i, 0)(s′′,si,0);
第一种边正常连边:(u,
v, c), (v, u, c)(u,v,c),(v,u,c);
第二种边连边:(a',
b'', l)(a′,b′′,l), (b',
a'', l)(b′,a′′,l)。
然后跑一遍 s-ts−t 最短路就是答案。
AC代码1:
把每个城市群也看成点,注意分成入点和出点。
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=60010;
#define LL long long
queue<int> q;
vector<pair<int,int> > to[maxn];
LL dis[maxn];
int n,m,in[maxn];
int main()
{
int x,y,z,w,s,t;
scanf("%d%d",&n,&m);
for (int i=1;i<=m;i++)
{
scanf("%d",&x);
while (x--)
{
scanf("%d",&y);
to[y].push_back(make_pair(i+n,0));
to[i+n+m].push_back(make_pair(y,0));
}
}
scanf("%d",&x);
while (x--)
{
scanf("%d%d%d",&y,&z,&w);
to[y].push_back(make_pair(z,w));
to[z].push_back(make_pair(y,w));
}
scanf("%d",&x);
while (x--)
{
scanf("%d%d%d",&y,&z,&w);
to[y+n].push_back(make_pair(z+n+m,w));
to[z+n].push_back(make_pair(y+n+m,w));
}
scanf("%d%d",&s,&t);
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
in[s]=1;
q.push(s);
while (!q.empty())
{
x=q.front();
q.pop();
for (vector<pair<int,int> >::iterator it=to[x].begin();it!=to[x].end();++it)
if (dis[x]+(*it).second<dis[(*it).first])
{
dis[(*it).first]=dis[x]+(*it).second;
if (!in[(*it).first])
{
q.push((*it).first);
in[(*it).first]=1;
}
}
in[x]=0;
}
if (dis[t]<1e12) printf("%lld\n",dis[t]);
else printf("-1\n");
}AC代码2:把每个城市群抽象成两个点 s′,s′′s′,s′′。按照如下方式见图:对于每个城市群里面的城市 sisi,连边:(si,s′,0)(si,s′,0), (s′′,si,0)(s′′,si,0);第一种边正常连边:(u,v,c),(v,u,c)(u,v,c),(v,u,c);第二种边连边:(a′,b′′,l)(a′,b′′,l), (b′,a′′,l)(b′,a′′,l)。然后跑一遍 s−ts−t 最短路就是答案。
#include <iostream>
#include <queue>
#include <algorithm>
#include <string.h>
#include <stdio.h>
using namespace std;
const int maxn = 100005;
const long long INF = 1e15;
int n, m, m1;
int visited[maxn];
long long dis[maxn];
vector<pair<int, long long>> map[maxn];
void add(int u, int v, int w) {
map[u].push_back({v, w});
}
void spfa(int start) {
for (int i = 1; i <= n + m*2; ++i)
dis[i] = INF;
visited[start] = 1;
dis[start] = 0;
queue<int> que;
que.push(start);
while (!que.empty()) {
int cur = que.front();
que.pop();
visited[cur] = 0;
for (int i = 0; i < map[cur].size(); ++i) {
if (dis[map[cur][i].first] > map[cur][i].second + dis[cur]) {
dis[map[cur][i].first] = map[cur][i].second + dis[cur];
if (!visited[map[cur][i].first]) {
visited[map[cur][i].first] = 1;
que.push(map[cur][i].first);
}
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
int k, u;
cin >> k;
while (k--) {
cin >> u;
add(u, n + i, 0);
add(n + m + i, u, 0);
}
}
cin >> m1;
for (int i = 1; i <= m1; ++i) {
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
add(v, u, w);
}
cin >> m1;
for (int i = 1; i <= m1; ++i) {
int u, v, w;
cin >> u >> v >> w;
add(u + n, v + n + m, w);
add(v + n, u + n + m, w);
}
int start, end;
cin >> start >> end;
spfa(start);
if (dis[end] == INF)
cout << -1 << endl;
else
cout << dis[end] << endl;
}
E题:商汤智能机器人
首先,可以判断,当 xx 与 yy 的和或差是奇数、或者 xx 小于 yy 时,答案为 00。对于其它情况,如果我们枚举走 \left
( a + 2,b \right )(a+2,b) 的步数,由组合数的知识,我们可以得出
ans=\sum_{i=0}^{min\left
( \frac{x+y}{2} , \frac{x - y}{2} \right )}\frac{\left ( x - i \right )!}{i!\left ( \frac{x+y}{2} - i \right )!\left ( \frac{x - y}{2} - i \right )!}ans=∑i=0min(2x+y,2x−y)i!(2x+y−i)!(2x−y−i)!(x−i)!
不妨令 n
= \frac{x+y}{2},n=2x+y, m
= \frac{x - y}{2}m=2x−y,且 n
\leq mn≤m。那么有
ans=\sum_{i=0}^{n}\frac{\left
( x - i \right )!}{i!\left ( n - i \right )!\left ( m - i \right )!} = \sum_{i=0}^{n}C_{x-i}^{i}C_{x-2i}^{n-i}ans=∑i=0ni!(n−i)!(m−i)!(x−i)!=∑i=0nCx−iiCx−2in−i
因为模数 pp 比较小,所以我们考虑对上述和式的每一项使用
Lucas 定理,那么第 ii 项就可以写成
C_{\left
( x-i \right )/p}^{i/p}C_{\left ( x-2i \right )/p}^{\left ( n-i \right )/p}C_{\left ( x-i \right )\%p}^{i\%p}C_{\left ( x-2i \right )\%p}^{\left ( n-i \right )\%p}=C_{\left ( x-i \right )/p}^{i/p} C_{\left ( x-i \right )/p-i/p}^{\left ( n-i \right )/p} C_{\left
( x-i \right )\%p}^{i\%p}C_{\left ( x-i \right )\%p-i\%p}^{\left ( n-i \right )\%p}C(x−i)/pi/pC(x−2i)/p(n−i)/pC(x−i)%pi%pC(x−2i)%p(n−i)%p=C(x−i)/pi/pC(x−i)/p−i/p(n−i)/pC(x−i)%pi%pC(x−i)%p−i%p(n−i)%p
可以证明,右式和左式是等价的。
然后,我们可以发现,对于第 ii 项和第 i+pi+p 项:
C_{\left
( x-i \right )\%p}^{i\%p}C_{\left ( x-i \right )\%p-i\%p}^{\left ( n-i \right )\%p}=C_{\left ( x-i-p \right )\%p}^{\left ( i+p \right )\%p}C_{\left ( x-i-p \right )\%p-\left ( i+p \right )\%p}^{\left ( n-i-p \right )\%p}C(x−i)%pi%pC(x−i)%p−i%p(n−i)%p=C(x−i−p)%p(i+p)%pC(x−i−p)%p−(i+p)%p(n−i−p)%p
那么,我们就可以将第 i,i+p,i+2p,i+3p\cdotsi,i+p,i+2p,i+3p⋯ 项进行合并,而对于它们不相同的部分,我们可以重复上述步骤进行合并。
最后,我们成功地将答案化为了 log_{p}xlogpx 个项数小于等于 pp 的和式的乘积,每一个和式都可以通过预处理在 O\left
( p \right )O(p) 的时间内计算出。
总体复杂度:O\left
( plog_{p}x \right )O(plogpx)。
F题:腾讯消消乐
用 f(mask,step)f(mask,step) 表示考虑当前 maskmask 集合内的数用 stepstep 步删除完的方案数,每次转移则可以简单地用 O(n^2)O(n2) 来进行枚举删掉的一段区间进行转移。直接暴力状压,O(2nn3)可以过。
#include<cstdio>
#include<algorithm>
using namespace std;
#define LL long long
const int p=1000000007,maxn=20;
int a[maxn],dp[300010][maxn],ok[300010],n,m;
int gcd(int x,int y)
{
return y?gcd(y,x%y):x;
}
int main()
{
int d,ans=0,x,y;
scanf("%d%d",&n,&m);
for (int i=0;i<n;i++) scanf("%d",&a[i]);
for (int s=1;s<(1<<n);s++)
{
x=0;
for (int i=0;i<n;i++)
if (s&(1<<i)) x=gcd(x,a[i]);
dp[s][1]=x>=m;
}
for (int s=1;s<(1<<n);s++)
for (int i=2;i<=n;i++)
for (int j=0;j<n;j++)
if (s&(1<<j))
{
x=y=0;
for (int k=j;k<n;k++)
if (s&(1<<k))
{
x=gcd(x,a[k]);
y|=1<<k;
if (x>=m) dp[s][i]=(dp[s][i]+dp[s^y][i-1])%p;
else break;
}
}
for (int i=1;i<=n;i++)
ans=(ans+(LL)dp[(1<<n)-1][i]*i)%p;
//dfs((1<<n)-1,10,n);
printf("%d\n",ans);
}
相关文章推荐
- 计蒜之道 2017 程序设计大赛 - 计蒜客 复赛 D 百度地图导航 最短路、Dijkstra的拓展
- 计蒜之道 2017 程序设计大赛 - 计蒜客 复赛 B Windows 画图 几何、平面、枚举
- 计蒜之道 2017 程序设计大赛 - 计蒜客 复赛 F 腾讯消消乐 状态压缩dp、枚举+剪枝
- 2017计蒜之道程序设计大赛初赛第四场题解
- 2017计蒜之道程序设计大赛初赛第五场
- star.baidu.com程序设计大赛初赛、复赛题目
- 2017计蒜之道程序设计大赛初赛第六场题解
- 2017计蒜之道程序设计大赛初赛第二场题解
- 2017计蒜之道程序设计大赛初赛第五场
- 2017计蒜之道程序设计大赛初赛第一场题解
- 2017计蒜之道程序设计大赛初赛第五场题解
- 2017计蒜之道程序设计大赛初赛第三场题解
- AIX 程序设计大赛---AIX正方形问题
- 2008程序设计大赛
- AIX 程序设计大赛---AIX正方形问题
- 程序设计大赛—页面置换算法(LRU)
- 程序设计大赛--约瑟夫问题
- 程序设计大赛-留下的学生
- AIX 程序设计大赛---AIX正方形问题
- AIX 程序设计大赛---AIX正方形问题
