二分类支持向量机模型SVM知识点详解

1 引言

在本篇博客中，你将会了解到支持向量机分类器名字的由来、它的基本假设、支持向量机针对线性可分、广义线性、非线性情况下的解决方法以及一些具体的推导过程，支持向量机常见问题的解答。在本篇博客的第二部分会给一幅支持向量机整个过程的流程图，从图中你可以清晰的了解到支持向量机模型针对不同情况的的创建和求解过程，以及他们之间的关系，在图中涉及到的关键细节知识，会在第三部分给出详细的说明。因此，即使你之前没有接触过SVM，在你认真读了该篇博客也会有一个清晰的支持向量机建模框架。在本篇博客的最后将会给出支持向量机SVM从建模到求解整个过程的python实现代码及测试结果。废话不多说，开启你的学霸模式吧~

2 SVM全流程示意图

下图主要展示了，支持向量机构建时原问题，对偶问题及求解过程



2.1 图说三种分类情况

图一展示了线性可分情况，如图所示，图二展示了存在少量误分类点的线性可分情况，图三展示了非线性分类情况。



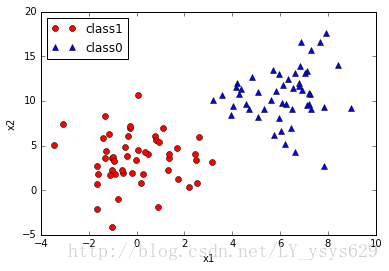
图1 线性可分情况



图2 线性不完全可分情况



图2非线性可分情况

2.2 7条说明详细解释SVM的关键知识点

说明1 –SVM的基本假设：

SVM模型是由少量几个样本点决定的，这几个样本点称为支持向量，支持向量距离超平面的距离是小于等于1的（原因后边有解释），假如SVM能够找出一个超平面或者超曲面使得支持向量能够尽可能的分类正确，且距离超平面或超曲面的距离尽可能的远，则非支持向量点，也能被正确分类且距离最远，该处距离的含义可认为分类正确的置信度，距离越远置信度越大。

说明2 –SVM的模型描述：

SVM模型超平面描述为： ww∗xx+b=0

决策函数f(x)=sign(ww∗xx+b)

为什么说策略是间隔最大？接下来会给出答案。

首先提一下两个概念：函数间隔和几何间隔（上述假设中的距离）

函数间隔：γ^i=yi(ww∗xi+b)

几何间隔：γi=γ^||ww||

（想象下点到线的距离,分类正确时，yi(ww∗xi+b)=||ww∗xi+b||）

假设，分类超平面已经确定，此时要找出距离超平面最短的样本点（支持向量点），可描述为：

γ=mini=1,2,...,nγi=mini=1,2,...,nγ^||ww||

根据假设，求该距离最大化时的超平面参数ww,b,描述为：

maxww,bγ等价于maxww,bγ^||ww||

maxww,bγ^||ww||s.t.yi(ww∗xi+b)≥γ^i=1,2,...,n,(1)

由于γ^对求解优化问题无影响，因此可令其为1γ^=1证明如下：

假设超平面参数为ww∗,b∗,支持向量样本点为(xmin,ymin),则支持向量的函数间隔为

γ^=ymin(ww∗xmin+b∗)(2)

由于超平面同时缩放所有参数不会改变，所以令ww∗=ww,γ^,b∗=b,γ^代入式（2）可得

1=ymin(ww,xmin+b,)(3)

因此，不管最后求得参数是多少，最后总能通过平移变换成函数间隔为1的情况，所以可以令函数间隔为1.

式（1）可变换为下式：

maxww,b1||ww||s.t.yi(ww∗xi+b)≥1i=1,2,...,n,(4)

最大化1||ww|| 和最小化12||ww||2是等价的，因此式(4)可以转变为如下所示：

minww,b12||ww||2s.t.yi(ww∗xi+b)−1≥0i=1,2,...,n,(5)

式（4）即为线性可分支持向量机原始问题。

由于约束是仿射函数（满足f(x)=a∗x+b,a∈Rn,x∈Rn,b∈Rn）,目标函数为二次凸函数，因此该问题为凸二次规划问题。

说明3,4 –不同情况的原始问题描述：

线性可分问题描述：

minww,b12||ww||2s.t.yi(ww∗xi+b)−1≥0i=1,2,...,n,(6)

线性不完全可分问题描述：

minww,b12||ww||2+C∑i=1nζis.t.yi(ww∗xi+b)≥1−ζii=1,2,...,n,ζi≥0,i=1,2,...,n,(7)

上式引入错分类惩罚系数C,表示使支持向量据超平面的间隔尽可能大的同时，减少错误分类的个数。

- 说明5–求解拉格朗日对偶问题：

拉格朗日对偶优化可参考拉格朗日对偶优化

由于式（4）是式（5）的一种特例，在此，只对式（5）求其对偶问题，球队欧问题可按如下步骤进行：

1）构造拉格朗日函数：

L（w,b,α,β,ζ）=12||ww||2+C∑i=1nζi−∑i=1nαi(yi(ww∗xi+b)−1+ζi)−∑i=1nμiζi(8)

其中，αi≥0,μi≥0

式（5）带有约束的最优化问题可转化为其拉格朗日函数的极大极小问题（参见 拉格朗日对偶优化可参考拉格朗日对偶优化）

即

maxα,βminww,b,ζL（ww,b,α,β,ζ）(9)

2）拉格朗日函数对原问题优化参数求偏导

∇wL（ww,b,α,β,ζ）=w−∑i=1nαiyixi=0∇bL（ww,b,α,β,ζ）=−∑i=1nαiyi=0∇ζL（ww,b,α,β,ζ）=C−αi−μi=0

由上式可得：

w=∑i=1nαiyixi(10)

∑i=1nαiyi=0(11)

C−αi−μi=0(12)

3）将式（9）-（10）代入拉格朗日函数加上约束即为对偶问题

minα∑i=1n∑j=1nαiαjyiyj(xi⋅xj)+∑j=1nαis.t.∑j=1nαiyi=00≤αi≤C,i=1,2,...,n,(13)

说明6–KKT条件求解参数：

利用SMO（序列最小最优算法）求解上述对偶问题的解为αα∗=(α∗1,α∗2,…,α∗n)

因为原始问题为凸二次规划问题，解满足KKT条件因此下式成立：

∇wL（ww∗,b∗,α∗,β∗,ζ∗）=w∗−∑i=1nα∗iyixi=0(14)

∇bL（ww∗,b∗,α∗,β∗,ζ∗）=−∑i=1nα∗iyi=0(15)

∇ζL（ww∗,b∗,α∗,β∗,ζ∗）=C−α∗i−μ∗i=0(16)

α∗i(yi(ww∗xi+b∗)−1+ζ∗i)=0(17)

μ∗iζ∗i=0(18)

yi(ww∗xi+b∗)−1+ζ∗i≥0(19)

ζ∗i≥0,α∗i≥0,μ∗i≥0(20)

由KKT互补条件可知：

若αi>0⇒yi(ww∗xi+b∗)−1+ζ∗i=0, μi≥0,⇒ζi=0

1）当αi=0表示对应的样本点对对偶问题没有影响，即对求解超平面参数没有影响，该样本点是非支持向量；

2）当0<α∗i<C时，由式（16）可知μ∗i>0,由KKT互补条件可知yi(ww∗xi+b∗)−1+ζ∗i=0,ζi=0,表明此刻αi对应的样本点为支持向量点

3）当α∗i=C时，由式（16）可知，μ∗i=0,ζi≤1表示正确分类的支持向量，1<ζi表示错误分类的支持向量。

由式（14）可知超平面权重向量为：

w∗=∑i=1nα∗iyixi

选择支持向量以及其对应的α来计算b∗

当0<α∗i<C时，yi(ww∗xi+b∗)−1+ζ∗i=0由此可知：

b∗=yj−∑i=1nyiα∗i(xi⋅xj)

说明7–利用SMO求解对偶问题：

在这片博客上有详细介绍SMO介绍

3 python实现

构造三种情况下的训练数据和测试数据程序在这里

python 实现基于SMO 的二分类SVM程序

# -*- coding: utf-8 -*-
"""
Created on Sat Jun 10 16:16:37 2017
SMO SVM
@author: liujiping
"""

import numpy as np
import matplotlib.pyplot as plt
import loadDataSet#读取数据集

def selectJrand(i,m):
j=i
while(j==i):
j = int(np.random.uniform(0,m))
return j

def clipAlpha(aj,H,L):
if aj > H: aj = H
if aj < L: aj = L
return aj

class optStruct:
'''
以类的形式，构建了一个包含重要、其他子函数常用变量的数据结构
'''
def __init__(self,dataMatIn,classLabels,C,toler,kernelOption=('linear',0)):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.n = np.shape(dataMatIn)[0]
#alpha为拉格朗日乘子，该向量的维数和训练样本个数相同，
#最后训练出来的非零alpha所对应的输入样本点为支持向量点
self.alphas = np.mat(np.zeros((self.n,1)))
self.b = 0
#E记录训练样本的标签差，第一列记录是否是更新的alpha计算的误差,0表示未进行
self.eCache = np.mat(np.zeros((self.n,2)))
self.kernelOption = kernelOption
self.kernelMat = calcKernelMatrix(self.X,self.kernelOption)

def calcKernelValue(matrix_X,sample_x,kernelOption):
'''
输入：训练数据集，样本点，核函数选项kernelOption=（'linear',0）or ('rbf',sigma),sigma>0
功能：计算特征样本间的乘积
输出：样本间乘积向量
'''
kernelType = kernelOption[0]
numSamples = matrix_X.shape[0]
kernelValue = np.mat(np.zeros((numSamples,1)))

if kernelType == 'linear':
kernelValue = matrix_X * sample_x.T
elif kernelType == 'rbf':
sigma = kernelOption[1]
if sigma == 0:
sigma = 1
for i in range(numSamples):
diff = matrix_X[i,:] - sample_x
kernelValue[i] = np.exp((diff * diff.T)/(-2.0 * sigma**2))
else:
raise NameError('not support kernel type! you can use ("linear",0) or ("rbf",1)')
return kernelValue

def calcKernelMatrix(matrix_X,kernelOption):
'''
输入：特征样本矩阵，核函数选项（包括线性核，高斯核等可自行在elif中添加）
功能: 计算在核函数作用下的特征样本映射矩阵
输出：映射矩阵
'''
numSamples = matrix_X.shape[0]
kernelMatirx = np.mat(np.zeros((numSamples,numSamples)))
for i in range(numSamples):
kernelMatirx[:,i] = calcKernelValue(matrix_X,matrix_X[i,:],kernelOption)
return kernelMatirx

def calcEk(oS, k):
'''
输入：optStruct数据对象，常数整型索引k
功能：计算更新第K个alpha后，利用第k个样本点计算的表现误差
输出：预测标签误差
'''
fXk = float(np.multiply(oS.alphas, oS.labelMat).T * oS.kernelMat[:,k]) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek

def selectJ(i,oS,Ei):
'''
输入：外层循环的选择的索引i, oS数据结构对象，外层循环对应的标签估计值误差
功能：在内层循环选出对应的外层循环alpha_i的alpha_j
输出：索引j,Ej
'''
#选择与外循环alpha求的Ei相差最大的alpha_j作为内循环变量
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei]#alpha_i已选出，置位Ei标志位
validEcacheList = np.nonzero(oS.eCache.A)[0]
if len(validEcacheList) > 1:
for k in validEcacheList:
if k == i :continue
Ek = calcEk(oS,k)
#选取步长最大
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
#只有一个alpha被计算时第二个alpha随机选取
else:
j = selectJrand(i,oS.n)
Ej = calcEk(oS,j)
return j,Ej

def updateEk(oS,k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]

def innerL(i,oS):#内循环程序
'''
输入：外层循环alpha所对应的下标，oS对象数据
功能：在第一个alpha选定情况下，根据最大步长启发式算法和KKT约束条件更新第二个alpha，之后在更新第一个alpha
输出：0或1,当有一对alpha更新时，返回1，其他返回0
'''
Ei = calcEk(oS, i)
#检验是否满足KKT条件，即当0<alpha<C时，yi*f(xi)=1是否成立
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or \
((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i,oS,Ei)
#后边需要新旧alpha的差值，因此需要另开辟空间保存旧的alpha值
alphaIold = oS.alphas[i].copy();alphaJold = oS.alphas[j].copy()
#利用旧的alpha值计算新的alpha值的上下限
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0,oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0,oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
#停止条件一，当上下限重合时，重新选择外循环alpha，为成功找到一队alpha因此返回0
if L == H: print 'L== H'; return 0
eta = 2.0 * oS.kernelMat[i,j] - oS.kernelMat[i,i] - oS.kernelMat[j,j]
#停止条件二
if (eta >= 0):print 'eta >= 0';return 0
#求无上下限的第二个alpha
oS.alphas[j] -= oS.labelMat[j] * (Ei- Ej)/eta
#加上上下限
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
#        updateEk(oS,j)
#停止条件三，当第二个alpha改变不大时
#        if (abs(oS.alphas[j] - alphaJold) <  0.0001):
#            print 'j not moving enough';return 0
if (abs(oS.alphas[j] - alphaJold) <  0.0001):
print 'j not moving enough'
updateEk(oS,j)
return 0
#计算新的第一个alpha值
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
#        updateEk(oS,i)
b1 = oS.b - Ei - oS.labelMat[i] *(oS.alphas[i] - alphaIold)* oS.kernelMat[i,i]-oS.labelMat[j]\
* (oS.alphas[j] - alphaJold)*oS.kernelMat[i,j]
b2 = oS.b - Ej - oS.labelMat[i] *(oS.alphas[i] - alphaIold)* oS.kernelMat[i,j]-oS.labelMat[j]\
* (oS.alphas[j] - alphaJold)*oS.kernelMat[j,j]
if (0 < oS.alphas[i]) and (oS.alphas[i] < oS.C): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.alphas[j] < oS.C): oS.b = b2
else:oS.b = (b1 + b2)/2.0
return 1
else:return 0

def smoP(dataMatIn,classLabels,C,toler,maxIter,kernelOption=('linear',0)):
'''
输入：特征数据集，标签向量，C：分类错误惩罚系数，Ei的误差容忍度，外层循环最大迭代次数，kTup默认是线性，波长为0
功能：实现SMO的外层循环
输出：分类超平面参数oS.b,拉格朗日乘子alpha向量
'''
oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler,kernelOption)
#初始化循环迭代变量
iter = 0
#初始化全部数据集遍历和非边界alpha调整的触发开关
entirSet = True; alphaPairsChanged =0
while(iter < maxIter) and ((alphaPairsChanged > 0) or (entirSet == True)):
alphaPairsChanged = 0
if entirSet:
for i in range(oS.n):
alphaPairsChanged += innerL(i,oS)
print "fullset, iter: %d i: %d ,pairs Changed %d" % (iter,i,alphaPairsChanged)
iter += 1
else:
nonBounIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBounIs:
alphaPairsChanged += innerL(i,oS)
print 'non-bound, iter:  %d i:  %d, pairsChanged  %d' % (iter,i,alphaPairsChanged)
iter += 1
#交替循环交替执行全集搜索与非边界搜索
if entirSet: entirSet = False
elif (alphaPairsChanged==0):entirSet = True
print "iterition number:  %d" % (iter)
return oS

def testSVM(oS,test_x,test_label):
test_x = np.mat(test_x)
test_label = np.mat(test_label)

numTestSamples = test_x.shape[0]
errorTrianCount = 0
errorTestCount = 0
predictTrain = np.mat(np.zeros((oS.n,1)))
predictTest = np.mat(np.zeros((numTestSamples,1)))

for i in range(oS.n):
predictTrain[i] = np.multiply(oS.alphas,oS.labelMat).T * oS.kernelMat[:,i] + oS.b
if np.sign(predictTrain[i]) != np.sign(oS.labelMat[i]):
errorTrianCount += 1
print 'the train error rate is %f\n'% (float(errorTrianCount)/float(oS.n))

for i in range(numTestSamples):
testKernelValue = calcKernelValue(oS.X,test_x[i,:],oS.kernelOption)
predictTest[i] = testKernelValue.T*np.multiply(oS.alphas,oS.labelMat) + oS.b

if np.sign(predictTest[i]) != np.sign(test_label[0,i]):
errorTestCount += 1
print 'the test error rate is %f\n'% (float(errorTestCount)/numTestSamples)
return predictTest

def showSVM(oS):
if oS.X.shape[1] != 2:
print 'this just is 2 dimention figure!'
return 1
#画出所有的样本点
for i in range(oS.n):
if oS.labelMat[i] == 1:
line1, = plt.plot(oS.X[i,0],oS.X[i,1],'or',label = 'class1')
elif oS.labelMat[i] == -1:
line2, = plt.plot(oS.X[i,0],oS.X[i,1],'ob',label = 'class-1')

#画出支持向量点
indexSupport = np.nonzero(oS.alphas.A > 0)[0]
for i in indexSupport:
plt.plot(oS.X[i,0],oS.X[i,1],'oy')
plt.legend(handles=[line1,line2],loc = 2)
plt.show()

if __name__ =='__main__':

#线性可分数据
#    filename = 'e:\python\ml\svm\svmLinearData.txt'
#    #近似线性数据
#    filename = 'e:\python\ml\svm\svmApproxiLinData.txt'
#非线性数据
filename = 'e:\python\ml\svm\svmNonLinearData.txt'
dataSet,labels = loadDataSet.loadDataSet(filename)
dataSet = np.mat(dataSet);labels = np.mat(labels)
trainDataSet1 = dataSet[:40,1:];trainLabels1 = labels[:,:40]
trainDataSet2 = dataSet[60:,1:];trainLabels2 = labels[:,60:]
trainDataSet = np.bmat('trainDataSet1;trainDataSet2');trainLabels = np.bmat('trainLabels1,trainLabels2')
testDataSet = dataSet[40:60,1:];testLabels = labels[:,40:60]

oS = smoP(trainDataSet,trainLabels,0.5,0.0001,40,('rbf',3))
predictTest = testSVM(oS,testDataSet,testLabels)
showSVM(oS)

the train error rate is 0.500000

the test error rate is 0.300000