CF - 801D. Volatile Kite - 计算几何
2017-04-20 20:20
375 查看
1.题目描述:
D. Volatile Kite
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given a convex polygon P with n distinct
vertices p1, p2, ..., pn.
Vertex pi has
coordinates (xi, yi) in
the 2D plane. These vertices are listed in clockwise order.
You can choose a real number D and move each vertex of the polygon a distance of at most D from
their original positions.
Find the maximum value of D such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.
Input
The first line has one integer n (4 ≤ n ≤ 1 000) —
the number of vertices.
The next n lines contain the coordinates of the vertices. Line i contains
two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) —
the coordinates of the i-th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon
(in particular, no three consecutive points lie on the same straight line).
Output
Print one real number D, which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely, let's assume that your answer is a and the answer of the jury is b.
The checker program will consider your answer correct if

.
Examples
input
output
input
output
Note
Here is a picture of the first sample
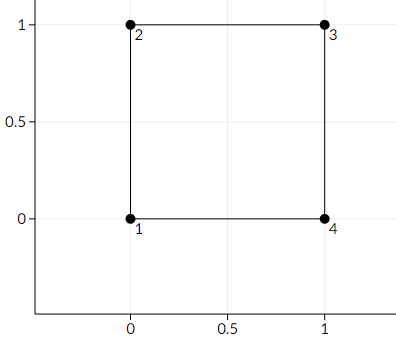
Here is an example of making the polygon non-convex.
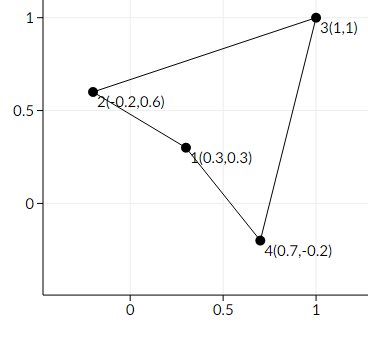
This is not an optimal solution, since the maximum distance we moved one point is ≈ 0.4242640687, whereas we can make it non-convex by only
moving each point a distance of at most ≈ 0.3535533906.
2.题意概述:
给你一个凸多边形,然后要你求最大的D,使得所有的点分别沿着任意方向移动D,多边形仍然是凸多边形。
3.解题思路:
对于相邻三个点,考虑移动中间那个点,当移动到它们三点共线时候一定是一个临界条件D,那么O(N)的更新每个顶点的临界条件即可。
对于到临界条件D的计算用到了叉乘。对于向量AxB表示以A和B为边的平行四边形面积,然后再算出这个平行四边形的高就是顶点移动到三点共线所需要移动的最小距离D。
4.AC代码:
#include <bits/stdc++.h>
#define INF 1e18
#define maxn 100100
#define lson root << 1
#define rson root << 1 | 1
#define lent (t[root].r - t[root].l + 1)
#define lenl (t[lson].r - t[lson].l + 1)
#define lenr (t[rson].r - t[rson].l + 1)
#define N 1111
#define eps 1e-6
#define pi acos(-1.0)
#define e exp(1.0)
using namespace std;
const int mod = 1e9 + 7;
typedef long long ll;
typedef unsigned long long ull;
struct point
{
double x, y;
point() {}
point(double a, double b) { x = a; y = b; }
friend point operator- (point a, point b)
{
return point(a.x - b.x, a.y - b.y);
}
friend point operator+ (point a, point b)
{
return point(a.x + b.x, a.y + b.y);
}
friend double operator* (point a, point b)
{
return a.x * b.y - b.x * a.y;
}
} p
;
double getdis(point a, point b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
long _begin_time = clock();
#endif
int n;
while (~scanf("%d", &n))
{
for (int i = 0; i < n; i++)
scanf("%lf%lf", &p[i].x, &p[i].y);
for (int i = n; i < n + 2; i++)
p[i] = p[i - n];
double ans = INF;
for (int i = 0; i < n; i++)
{
double tmp = (p[i + 2] - p[i]) * (p[i + 1] - p[i]) / 2.0 / getdis(p[i + 2], p[i]);
ans = min(ans, tmp);
}
printf("%.10f\n", ans);
}
#ifndef ONLINE_JUDGE
long _end_time = clock();
printf("time = %ld ms.", _end_time - _begin_time);
#endif
return 0;
}
D. Volatile Kite
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given a convex polygon P with n distinct
vertices p1, p2, ..., pn.
Vertex pi has
coordinates (xi, yi) in
the 2D plane. These vertices are listed in clockwise order.
You can choose a real number D and move each vertex of the polygon a distance of at most D from
their original positions.
Find the maximum value of D such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.
Input
The first line has one integer n (4 ≤ n ≤ 1 000) —
the number of vertices.
The next n lines contain the coordinates of the vertices. Line i contains
two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) —
the coordinates of the i-th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon
(in particular, no three consecutive points lie on the same straight line).
Output
Print one real number D, which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely, let's assume that your answer is a and the answer of the jury is b.
The checker program will consider your answer correct if

.
Examples
input
4 0 0 0 1 1 1 1 0
output
0.3535533906
input
6 5 0 10 0 12 -4 10 -8 5 -8 3 -4
output
1.0000000000
Note
Here is a picture of the first sample

Here is an example of making the polygon non-convex.

This is not an optimal solution, since the maximum distance we moved one point is ≈ 0.4242640687, whereas we can make it non-convex by only
moving each point a distance of at most ≈ 0.3535533906.
2.题意概述:
给你一个凸多边形,然后要你求最大的D,使得所有的点分别沿着任意方向移动D,多边形仍然是凸多边形。
3.解题思路:
对于相邻三个点,考虑移动中间那个点,当移动到它们三点共线时候一定是一个临界条件D,那么O(N)的更新每个顶点的临界条件即可。
对于到临界条件D的计算用到了叉乘。对于向量AxB表示以A和B为边的平行四边形面积,然后再算出这个平行四边形的高就是顶点移动到三点共线所需要移动的最小距离D。
4.AC代码:
#include <bits/stdc++.h>
#define INF 1e18
#define maxn 100100
#define lson root << 1
#define rson root << 1 | 1
#define lent (t[root].r - t[root].l + 1)
#define lenl (t[lson].r - t[lson].l + 1)
#define lenr (t[rson].r - t[rson].l + 1)
#define N 1111
#define eps 1e-6
#define pi acos(-1.0)
#define e exp(1.0)
using namespace std;
const int mod = 1e9 + 7;
typedef long long ll;
typedef unsigned long long ull;
struct point
{
double x, y;
point() {}
point(double a, double b) { x = a; y = b; }
friend point operator- (point a, point b)
{
return point(a.x - b.x, a.y - b.y);
}
friend point operator+ (point a, point b)
{
return point(a.x + b.x, a.y + b.y);
}
friend double operator* (point a, point b)
{
return a.x * b.y - b.x * a.y;
}
} p
;
double getdis(point a, point b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
long _begin_time = clock();
#endif
int n;
while (~scanf("%d", &n))
{
for (int i = 0; i < n; i++)
scanf("%lf%lf", &p[i].x, &p[i].y);
for (int i = n; i < n + 2; i++)
p[i] = p[i - n];
double ans = INF;
for (int i = 0; i < n; i++)
{
double tmp = (p[i + 2] - p[i]) * (p[i + 1] - p[i]) / 2.0 / getdis(p[i + 2], p[i]);
ans = min(ans, tmp);
}
printf("%.10f\n", ans);
}
#ifndef ONLINE_JUDGE
long _end_time = clock();
printf("time = %ld ms.", _end_time - _begin_time);
#endif
return 0;
}
相关文章推荐
- CF - 497D. Gears - 计算几何+暴力 - Mutual Training for Wannafly Union #7
- cf#Wunder Fund Round 2016 -C - Constellation-计算几何-水题
- CF 333E 计算几何+bitset优化
- VK Cup 2017 B. Volatile Kite (Div . 1)(凸多边形退化)(计算几何)
- cf 342C - Cupboard and Balloons(计算几何)
- 【BZOJ1069】【SCOI2007】最大土地面积 计算几何 凸包
- 【POJ2504】Bounding box(计算几何)
- 计算几何之判断线段相交
- 板子:计算几何
- 计算几何-经典算法-凸包
- uva 11800 Determine the Shape 判断四边形形状(计算几何)
- 【计算几何】线段相交
- 计算几何--判断点是否在矩形里
- 计算几何模板
- Java经典编程300例之实例061 计算几何图形的面积(抽象类)
- 洛谷 P1355 神秘大三角(计算几何基础)
- Tell me the area(计算几何--求两圆相交面积)
- POJ2318二分加计算几何之我爱叉乘~+poj2398
- 计算几何的简单模板
- ZOJ 1648 Circuit Board(计算几何)
