Supervised Descent Method(人脸对齐之SDM论文解析)
2017-03-31 22:51
1176 查看
Supervised Descent Method(人脸对齐之SDM论文解析)
标签: SDM NLS Jacobian Hessian FaceAlignment
作者:贾金让
本人博客链接:http://blog.csdn.net/jiajinrang93
文章来源:2013CVPR
文章作者:Xuehan Xiong,Fernando De la Torre
简要介绍:这篇文章主要提出了一种名为SDM(Supervised Descent Method)的方法,用来最小化非线性最小二乘(Non-linear Least Squares)目标函数,即目标函数是均方误差。SDM方法通过学习得到一系列下降的方向和该方向上的尺度,使得目标函数以非常快的速度收敛到最小值,回避了求解Jacobian矩阵和Hessian矩阵的问题。下面开始详细介绍,我补充了文章中只给出结果的推导过程,并且稍微调整了一下文章中牛顿步的推导过程。
那么什么是牛顿步方法呢?下面简单介绍一下牛顿步,后面还会详细推导牛顿步。
牛顿步:在Hessian矩阵正定的情况下,极小值可以通过求解线性方程组来迭代求解。给定一个初始的估计值x0∈Rp×1,牛顿步的更新迭代公式如下:
xk+1=xk−H−1(xk)Jf(xk)(1)
其中H−1(xk)∈Rp×p是在xk点的Hessian矩阵,Jf(xk)∈Rp×1是 在xk点的 Jacobian矩阵。
牛顿步方法有两个主要优点:
1. 如果牛顿步可以收敛,那么它的收敛速度是二次的,收敛速度非常快。
2. 如果初始点在最小点邻域附近,那么它一定可以收敛。
但牛顿法在应用中,也有几个缺点:
1. Hessian矩阵在极小值附近是局部正定的,但可能不是全局正定的,这就会导致牛顿步并不一定朝向下降的方向。
2. 牛顿步需要函数二次可导。这个要求在实际应用中是一个很强的要求,比如图像处理中经常被使用的SIFT特征,它可以被看成是一个不可导的特征,因此在这种情况下,在我们只能通过数值逼近下降的方向或者是Hessian矩阵,但这种计算代价非常大。
3. 由于Hessian矩阵通常很大,计算它的逆矩阵代价是非常大的,复杂度通常是O(p3)。
以上三个缺陷使我们在实际应用中,很难计算精确的Hessian矩阵,甚至连数值逼近都是很困难的(由于计算代价比较大)。因此,该文章提出了SDM方法,用数据来学习下降的方向。下面两张图可以用来初步表示牛顿步和SDM两种方法的基本原理。
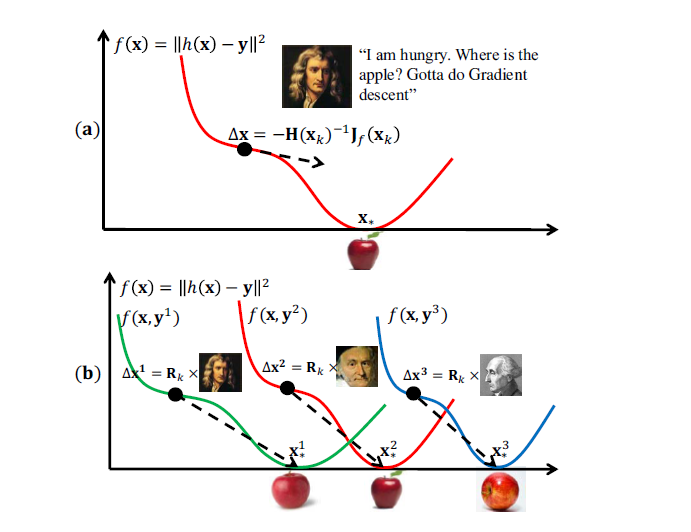
人脸对齐(Face Alignment)基本原理:
基本概念:人脸识别(face recognizaton)按顺序可以大体上分为四个部分,即人脸检测(face detection),人脸对齐(face alignment),人脸校验(face verification)和人脸识别(face identification)。 人脸检测就是在一张图片中找到人脸所处的位置,即将人脸圈出来,比如拍照时数码相机自动画出人脸。人脸对齐就是在已经检测到的人脸的基础上,自动找到人脸上的眼睛鼻子嘴和脸轮廓等标志性特征位置。人脸校验就是判断两张脸是不是同一个人。人脸识别就是给定一张脸,判断这张脸是谁。
本文研究其中的第二部分,人脸对齐。
人脸对齐中的几个关键词:
形状(shape):形状就是人脸上的有特征的位置,如下图所示,每张图中所有黄点构成的图形就是该人脸的形状。
特征点(landmark):形状由特征点组成,图中的每一个黄点就是一个特征点。

人脸对齐的最终目的就是在已知的人脸方框(一般由人脸检测确定人脸的位置)上定位其准确地形状。
人脸对齐的算法主要分为两大类:基于优化的方法(Optimization-based method)和基于回归的方法(Regression-based method)。
SDM方法属于基于回归的方法。
基于回归的方法的基本原理:对于一张给定的人脸,给出一个初始的形状,通过不断地迭代,将初始形状回归到接近甚至等于真实形状的位置。
f(x0+Δx)=||h(d(x0+Δx))−ϕ∗||22(2)
其中ϕ∗=h(d(x∗))表示该人脸的真实特征点所提取出的SIFT特征,当然,上面说的是在预测时我们的目标,在预测时我们只有初始的x0,而Δx和ϕ∗我们是不知道的。在训练时,我们是知道Δx和ϕ∗的,我们要在训练时训练得到一个良好的回归器,使它能够让初始的x0一步步回归到正确的未知的形状上去。一般来说初始的x0就是所有已知样本的真实形状的平均形状。示意图如下图所示。
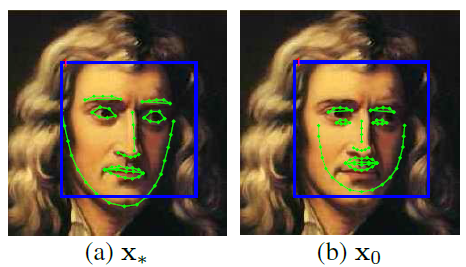
那么问题来了,如果每一张脸的初始形状都是一样的(即都是已知样本的真实形状的平均形状),那么怎么让它们回归到各自人脸的真实形状呢,答案就是每张图片提取出的不同的SIFT特征(具体采用什么特征可以依据情况而定,论文中 采用了SIFT特征,但也可以采用如HOG,DOG,甚至LBF等特征)了,虽然采用了相同的初始形状,但在不同的图片上,相同的初始形状所提取出的SIFT特征是完全不同的,也就是ϕ0是不同的,这样就可以通过回归器将其回归到各自的真实形状上了。这一点通过上面的公式也能看出。
现在我们已经有了优化的目标,就是要得到一个回归器,这个回归器能起到的作用是将一个初始形状回归到真实形状上去。也就是学到正确的回归器使其得到最好的Δx 。当然想要从初始形状一步步回归到真实形状,只学习一个Δx一般是不行的,因为一步就回归到最小点一般来说要求比较高,即使是牛顿步回归的比较快,通常也不能一步就达到目标。所以我们要学习得到多个不同的回归器,它们依次回归下来,能得到一系列的Δx,这样我们就能很快根据xk+1=xk+Δx得到使目标函数最小的点。
下面从牛顿步开始引出SDM。
首先再写一遍目标函数,如下:
f(x0+Δx)=||h(d(x0+Δx))−ϕ∗||22(3)
我们使用的是从初始特征点周围提取的SIFT特征作为第一次回归的输入,然而SIFT算子是不可导的,所以如果想要使用一阶或者二阶方法来最小化上面的目标函数,那就只能用数值逼近的方法来估计Jacobian和Hessian矩阵(比如有限差分方法等)。然而数值估计计算量非常大,所以我们要采用SDM方法来学习下降的方向和下降的尺度,或者说学习Jaobian和Hessian矩阵。
为了从牛顿步开始引出SDM,我们首先假设h()这个SIFT特征提取函数是二次可导的。这样才能计算Hessian矩阵。
以下部分推导和论文不同,论文中只给了结论,我补充了论文没有写的推导过程。同时优化了一下牛顿步的推导过程。
第一步,我们首先获得一个初始的形状x0,采用的方式是用所有训练样本的真实形状的平均形状给x0赋值,也就是说我们迭代的初值为:
x0=1N∑Ni=1x∗i(4)
接着就可以根据公式(3)计算f(x0),即令Δx=0。
现在我们已经有了f(x0),我们想要知道朝什么样的方向改变x0并且改变多少x0可以得到一个好的f(x1),使f(x1)尽量接近全局最小值,这里f(x1)=f(x0+Δx)。
我们在x0点对f(x)进行二阶泰勒展开,如下:
f(x)=f(x0)+Jf(x0)T(x−x0)+12(x−x0)TH(x0)(x−x0)+o(|x−x0|2)(5)
等式最右边一项是高阶项,可以忽略。也就是说,我们要优化的目标,就是下面这个二次型,我们要极小化下面的二次型:
f(x)=f(x0)+Jf(x0)T(x−x0)+12(x−x0)TH(x0)(x−x0)(6)
因为要极小化f(x),所以我们要对x进行求导,并且令导数等于0,以此来求出优化的方向和大小,下面对每一项进行求导:
df(x)dx=∇f(x)(7)
df(x0)dx=0(8)
dJf(x0)T(x−x0)dx=Jf(x0)(9)
d12(x−x0)TH(x0)(x−x0)dx=12[H(x0)+H(x0)T](x−x0)=H(x0)(x−x0)(10)
因此,求导后得到:
∇f(x)=0+Jf(x0)+H(x0)(x−x0)(11)
令导数等于0,得:
∇f(x)=Jf(x0)+H(x0)(x−x0)=0(12)
可以解得:
x=x0−H−1(x0)Jf(x0)(13)
即
x1=x0−H−1(x0)Jf(x0)(14)
这即得到牛顿步的表达式。
我们的第一次迭代的步长用牛顿步的方法求解就是:
Δx1=−H−1(x0)Jf(x0)(15)
如果在目标函数二次可导的情况下,一直使用牛顿步计算出Δx2、Δx3、…、Δxk,那么可以根据更新表达式(如下)一直计算得到新的x,直到得到最优解。
xk+1=xk+Δxk(16)
不过使用牛顿步计算几个Δx就要算几次Jacobian和Hessian矩阵,计算量之大可想而知了,况且目标函数还不一定二次可导(之前的二次可导是我们假设的,现在我们将去掉二次可导这个约束条件)。
下面开始推导得到我们要的SDM的方法,是接着上面牛顿步的推导而来的:
首先引入矩阵的链式求导法则如下:
df(g(x))dx=dgT(x)dxdf(g)dg(17)
应用矩阵的链式求导法则:
Jf(x0)=df(x)dx|x=x0=d||h(d(x))−ϕ∗||22dx|x=x0=d(ϕx−ϕ∗)Tdx|x=x0⋅d||ϕx−ϕ∗||22d(ϕx−ϕ∗)|x=x0
(18)
其中:
d(ϕx−ϕ∗)Tdx|x=x0=dϕTxdx|x=x0=dhT(d(x))dx|x=x0=JTh(x0)(19)
d||ϕx−ϕ∗||22d(ϕx−ϕ∗)|x=x0=d[(ϕx−ϕ∗)T(ϕx−ϕ∗)]d(ϕx−ϕ∗)|x=x0=2(ϕx−ϕ∗)|x=x0=2(ϕ0−ϕ∗)(20)
所以:
Jf(x0)=2JTh(x0)(ϕ0−ϕ∗)(21)
因此
x=x0−H−1(x0)Jf(x0)=x0−2H−1(x0)JTh(x0)(ϕ0−ϕ∗)(22)
所以我们的SDM方法的Δx1为:
Δx1=−2H−1(x0)JTh(x0)(ϕ0−ϕ∗)(23)
看起来好像和牛顿步的Δx1=−H−1(x0)Jf(x0)区别不大,然而接下来就会看到区别:
Δx1=−2H−1(x0)JTh(x0)(ϕ0−ϕ∗)=Δx1=−2H−1(x0)JTh(x0)ϕ0−2H−1(x0)JTh(x0)ϕ∗
(24)
设R0=−2H−1(x0)JTh(x0),b0=−2H−1(x0)JTh(x0)ϕ∗,可将上式表示成:
Δx1=R0ϕ0+b0(25)
也就是说,第一次增量Δx1变成了特征ϕ0的一次函数,而我们只需要知道R0和b0就可以直接算出第一次的增量Δx1!!!
也许有人会问,但是根据你前面的公式,你的R0和b0也是在计算Jacobian和Hessian矩阵的基础上计算出来的啊,说的没错,但既然现在已经将目标Δx1写成了ϕ0的一次函数,我们计算的R0和b0难道还要绕回去算Jacobian和Hessian矩阵么,当然不可能了,我们只需要用我们最常用的方法,最小二乘即可!!
即最小化下面这个目标函数:
loss=||Δx1−R0ϕ0−b0||22(26)
此时可以由最小二乘的公式直接得到R0和b0,这里就不写了。
得到了R0和b0,也就可以依法得到R1、b1、…、Rk和bk,也就可以算出对应的的Δx2、…、Δxk+1,这些Δx就是我们要的每一次的x的变化方向和变化的尺度,也是根据更新公式更新,直到得到最小点的x。
有了R1、b1、…、Rk和bk,在测试样本进行回归的时候,就可以直接进行回归。
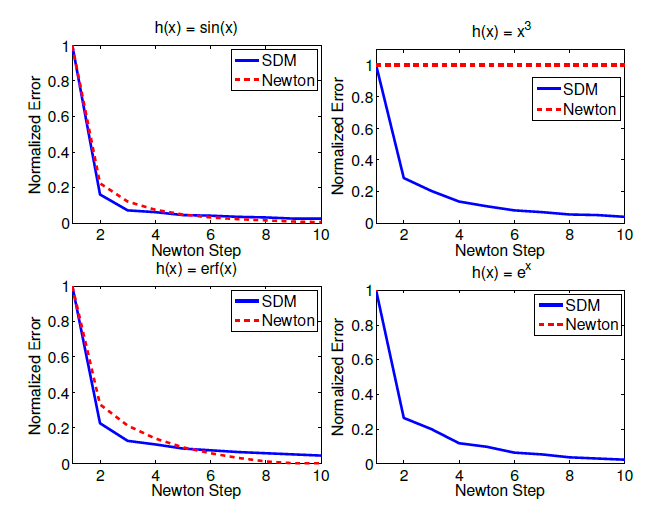
下图是作者做的对比试验(控制的变量是特征提取函数h()不同):
有图可见,SDM的收敛速度比牛顿步更快,只是收敛得最终结果并没有达到最优(比牛顿步差一点),但SDM更具鲁棒性,在函数的Hessian矩阵不是正定的时候,SDM也能很快收敛。
做个总结:
SDM方法在更新x时,就是将更新的增量Δx的计算方法进行了改变,由牛顿步的计算Jacobian和Hessian矩阵来得到增量Δx,变成了计算Rk和bk来得到增量Δx,通过推导将每一次的增量Δx变成了该次输入的特征ϕ的一次函数,并通过最小二乘直接计算一次函数的系数Rk和bk,大大减少了计算量。
标签: SDM NLS Jacobian Hessian FaceAlignment
作者:贾金让
本人博客链接:http://blog.csdn.net/jiajinrang93
1.概述
文章名称:Supervised Descent Method and its Applications to Face Alignment文章来源:2013CVPR
文章作者:Xuehan Xiong,Fernando De la Torre
简要介绍:这篇文章主要提出了一种名为SDM(Supervised Descent Method)的方法,用来最小化非线性最小二乘(Non-linear Least Squares)目标函数,即目标函数是均方误差。SDM方法通过学习得到一系列下降的方向和该方向上的尺度,使得目标函数以非常快的速度收敛到最小值,回避了求解Jacobian矩阵和Hessian矩阵的问题。下面开始详细介绍,我补充了文章中只给出结果的推导过程,并且稍微调整了一下文章中牛顿步的推导过程。
2.从牛顿步说起
数值优化在很多领域都有很重要的应用,计算机视觉中很多重要的问题比如(行人跟踪、人脸对齐等)都可以化成非线性优化问题来解决。解决非线性优化的方法有很多,其中非常常用的有基于一阶的或者是二阶的优化方法,比如梯度下降方法、牛顿步、LM算法等等。尽管很多年过去了,在二阶导可求得情况下,牛顿步仍然被认为是一个非常优秀的算法。那么什么是牛顿步方法呢?下面简单介绍一下牛顿步,后面还会详细推导牛顿步。
牛顿步:在Hessian矩阵正定的情况下,极小值可以通过求解线性方程组来迭代求解。给定一个初始的估计值x0∈Rp×1,牛顿步的更新迭代公式如下:
xk+1=xk−H−1(xk)Jf(xk)(1)
其中H−1(xk)∈Rp×p是在xk点的Hessian矩阵,Jf(xk)∈Rp×1是 在xk点的 Jacobian矩阵。
牛顿步方法有两个主要优点:
1. 如果牛顿步可以收敛,那么它的收敛速度是二次的,收敛速度非常快。
2. 如果初始点在最小点邻域附近,那么它一定可以收敛。
但牛顿法在应用中,也有几个缺点:
1. Hessian矩阵在极小值附近是局部正定的,但可能不是全局正定的,这就会导致牛顿步并不一定朝向下降的方向。
2. 牛顿步需要函数二次可导。这个要求在实际应用中是一个很强的要求,比如图像处理中经常被使用的SIFT特征,它可以被看成是一个不可导的特征,因此在这种情况下,在我们只能通过数值逼近下降的方向或者是Hessian矩阵,但这种计算代价非常大。
3. 由于Hessian矩阵通常很大,计算它的逆矩阵代价是非常大的,复杂度通常是O(p3)。
以上三个缺陷使我们在实际应用中,很难计算精确的Hessian矩阵,甚至连数值逼近都是很困难的(由于计算代价比较大)。因此,该文章提出了SDM方法,用数据来学习下降的方向。下面两张图可以用来初步表示牛顿步和SDM两种方法的基本原理。

3.人脸对齐的几个概念(简单介绍)
在介绍SDM之前,还要先简单提一下人脸识别中人脸对齐的基本原理和相关的关键词,因为该SDM方法主要是在人脸对齐方面进行应用。人脸对齐(Face Alignment)基本原理:
基本概念:人脸识别(face recognizaton)按顺序可以大体上分为四个部分,即人脸检测(face detection),人脸对齐(face alignment),人脸校验(face verification)和人脸识别(face identification)。 人脸检测就是在一张图片中找到人脸所处的位置,即将人脸圈出来,比如拍照时数码相机自动画出人脸。人脸对齐就是在已经检测到的人脸的基础上,自动找到人脸上的眼睛鼻子嘴和脸轮廓等标志性特征位置。人脸校验就是判断两张脸是不是同一个人。人脸识别就是给定一张脸,判断这张脸是谁。
本文研究其中的第二部分,人脸对齐。
人脸对齐中的几个关键词:
形状(shape):形状就是人脸上的有特征的位置,如下图所示,每张图中所有黄点构成的图形就是该人脸的形状。
特征点(landmark):形状由特征点组成,图中的每一个黄点就是一个特征点。

人脸对齐的最终目的就是在已知的人脸方框(一般由人脸检测确定人脸的位置)上定位其准确地形状。
人脸对齐的算法主要分为两大类:基于优化的方法(Optimization-based method)和基于回归的方法(Regression-based method)。
SDM方法属于基于回归的方法。
基于回归的方法的基本原理:对于一张给定的人脸,给出一个初始的形状,通过不断地迭代,将初始形状回归到接近甚至等于真实形状的位置。
4.Supervised Descent Method
给定一张含有m个像素的图片d∈Rm×1,d(x)∈Rp×1表示该图片上的p个特征点,h()表示一个非线性特征提取函数,比如h(d(x))∈R128p×1可以表示从p个特征点上提取出的SIFT特征,每个特征点提取出了128个SIFT特征。那么我们的目标就是,在给定一个初始形状x0的基础上,通过回归的方法,将x0回归到该人脸正确的形状x∗上,用数学的方式表达,即为求得使下面的f(x0+Δx)最小的Δx。f(x0+Δx)=||h(d(x0+Δx))−ϕ∗||22(2)
其中ϕ∗=h(d(x∗))表示该人脸的真实特征点所提取出的SIFT特征,当然,上面说的是在预测时我们的目标,在预测时我们只有初始的x0,而Δx和ϕ∗我们是不知道的。在训练时,我们是知道Δx和ϕ∗的,我们要在训练时训练得到一个良好的回归器,使它能够让初始的x0一步步回归到正确的未知的形状上去。一般来说初始的x0就是所有已知样本的真实形状的平均形状。示意图如下图所示。

那么问题来了,如果每一张脸的初始形状都是一样的(即都是已知样本的真实形状的平均形状),那么怎么让它们回归到各自人脸的真实形状呢,答案就是每张图片提取出的不同的SIFT特征(具体采用什么特征可以依据情况而定,论文中 采用了SIFT特征,但也可以采用如HOG,DOG,甚至LBF等特征)了,虽然采用了相同的初始形状,但在不同的图片上,相同的初始形状所提取出的SIFT特征是完全不同的,也就是ϕ0是不同的,这样就可以通过回归器将其回归到各自的真实形状上了。这一点通过上面的公式也能看出。
现在我们已经有了优化的目标,就是要得到一个回归器,这个回归器能起到的作用是将一个初始形状回归到真实形状上去。也就是学到正确的回归器使其得到最好的Δx 。当然想要从初始形状一步步回归到真实形状,只学习一个Δx一般是不行的,因为一步就回归到最小点一般来说要求比较高,即使是牛顿步回归的比较快,通常也不能一步就达到目标。所以我们要学习得到多个不同的回归器,它们依次回归下来,能得到一系列的Δx,这样我们就能很快根据xk+1=xk+Δx得到使目标函数最小的点。
下面从牛顿步开始引出SDM。
首先再写一遍目标函数,如下:
f(x0+Δx)=||h(d(x0+Δx))−ϕ∗||22(3)
我们使用的是从初始特征点周围提取的SIFT特征作为第一次回归的输入,然而SIFT算子是不可导的,所以如果想要使用一阶或者二阶方法来最小化上面的目标函数,那就只能用数值逼近的方法来估计Jacobian和Hessian矩阵(比如有限差分方法等)。然而数值估计计算量非常大,所以我们要采用SDM方法来学习下降的方向和下降的尺度,或者说学习Jaobian和Hessian矩阵。
为了从牛顿步开始引出SDM,我们首先假设h()这个SIFT特征提取函数是二次可导的。这样才能计算Hessian矩阵。
以下部分推导和论文不同,论文中只给了结论,我补充了论文没有写的推导过程。同时优化了一下牛顿步的推导过程。
第一步,我们首先获得一个初始的形状x0,采用的方式是用所有训练样本的真实形状的平均形状给x0赋值,也就是说我们迭代的初值为:
x0=1N∑Ni=1x∗i(4)
接着就可以根据公式(3)计算f(x0),即令Δx=0。
现在我们已经有了f(x0),我们想要知道朝什么样的方向改变x0并且改变多少x0可以得到一个好的f(x1),使f(x1)尽量接近全局最小值,这里f(x1)=f(x0+Δx)。
我们在x0点对f(x)进行二阶泰勒展开,如下:
f(x)=f(x0)+Jf(x0)T(x−x0)+12(x−x0)TH(x0)(x−x0)+o(|x−x0|2)(5)
等式最右边一项是高阶项,可以忽略。也就是说,我们要优化的目标,就是下面这个二次型,我们要极小化下面的二次型:
f(x)=f(x0)+Jf(x0)T(x−x0)+12(x−x0)TH(x0)(x−x0)(6)
因为要极小化f(x),所以我们要对x进行求导,并且令导数等于0,以此来求出优化的方向和大小,下面对每一项进行求导:
df(x)dx=∇f(x)(7)
df(x0)dx=0(8)
dJf(x0)T(x−x0)dx=Jf(x0)(9)
d12(x−x0)TH(x0)(x−x0)dx=12[H(x0)+H(x0)T](x−x0)=H(x0)(x−x0)(10)
因此,求导后得到:
∇f(x)=0+Jf(x0)+H(x0)(x−x0)(11)
令导数等于0,得:
∇f(x)=Jf(x0)+H(x0)(x−x0)=0(12)
可以解得:
x=x0−H−1(x0)Jf(x0)(13)
即
x1=x0−H−1(x0)Jf(x0)(14)
这即得到牛顿步的表达式。
我们的第一次迭代的步长用牛顿步的方法求解就是:
Δx1=−H−1(x0)Jf(x0)(15)
如果在目标函数二次可导的情况下,一直使用牛顿步计算出Δx2、Δx3、…、Δxk,那么可以根据更新表达式(如下)一直计算得到新的x,直到得到最优解。
xk+1=xk+Δxk(16)
不过使用牛顿步计算几个Δx就要算几次Jacobian和Hessian矩阵,计算量之大可想而知了,况且目标函数还不一定二次可导(之前的二次可导是我们假设的,现在我们将去掉二次可导这个约束条件)。
下面开始推导得到我们要的SDM的方法,是接着上面牛顿步的推导而来的:
首先引入矩阵的链式求导法则如下:
df(g(x))dx=dgT(x)dxdf(g)dg(17)
应用矩阵的链式求导法则:
Jf(x0)=df(x)dx|x=x0=d||h(d(x))−ϕ∗||22dx|x=x0=d(ϕx−ϕ∗)Tdx|x=x0⋅d||ϕx−ϕ∗||22d(ϕx−ϕ∗)|x=x0
(18)
其中:
d(ϕx−ϕ∗)Tdx|x=x0=dϕTxdx|x=x0=dhT(d(x))dx|x=x0=JTh(x0)(19)
d||ϕx−ϕ∗||22d(ϕx−ϕ∗)|x=x0=d[(ϕx−ϕ∗)T(ϕx−ϕ∗)]d(ϕx−ϕ∗)|x=x0=2(ϕx−ϕ∗)|x=x0=2(ϕ0−ϕ∗)(20)
所以:
Jf(x0)=2JTh(x0)(ϕ0−ϕ∗)(21)
因此
x=x0−H−1(x0)Jf(x0)=x0−2H−1(x0)JTh(x0)(ϕ0−ϕ∗)(22)
所以我们的SDM方法的Δx1为:
Δx1=−2H−1(x0)JTh(x0)(ϕ0−ϕ∗)(23)
看起来好像和牛顿步的Δx1=−H−1(x0)Jf(x0)区别不大,然而接下来就会看到区别:
Δx1=−2H−1(x0)JTh(x0)(ϕ0−ϕ∗)=Δx1=−2H−1(x0)JTh(x0)ϕ0−2H−1(x0)JTh(x0)ϕ∗
(24)
设R0=−2H−1(x0)JTh(x0),b0=−2H−1(x0)JTh(x0)ϕ∗,可将上式表示成:
Δx1=R0ϕ0+b0(25)
也就是说,第一次增量Δx1变成了特征ϕ0的一次函数,而我们只需要知道R0和b0就可以直接算出第一次的增量Δx1!!!
也许有人会问,但是根据你前面的公式,你的R0和b0也是在计算Jacobian和Hessian矩阵的基础上计算出来的啊,说的没错,但既然现在已经将目标Δx1写成了ϕ0的一次函数,我们计算的R0和b0难道还要绕回去算Jacobian和Hessian矩阵么,当然不可能了,我们只需要用我们最常用的方法,最小二乘即可!!
即最小化下面这个目标函数:
loss=||Δx1−R0ϕ0−b0||22(26)
此时可以由最小二乘的公式直接得到R0和b0,这里就不写了。
得到了R0和b0,也就可以依法得到R1、b1、…、Rk和bk,也就可以算出对应的的Δx2、…、Δxk+1,这些Δx就是我们要的每一次的x的变化方向和变化的尺度,也是根据更新公式更新,直到得到最小点的x。
有了R1、b1、…、Rk和bk,在测试样本进行回归的时候,就可以直接进行回归。
下图是作者做的对比试验(控制的变量是特征提取函数h()不同):
有图可见,SDM的收敛速度比牛顿步更快,只是收敛得最终结果并没有达到最优(比牛顿步差一点),但SDM更具鲁棒性,在函数的Hessian矩阵不是正定的时候,SDM也能很快收敛。

做个总结:
SDM方法在更新x时,就是将更新的增量Δx的计算方法进行了改变,由牛顿步的计算Jacobian和Hessian矩阵来得到增量Δx,变成了计算Rk和bk来得到增量Δx,通过推导将每一次的增量Δx变成了该次输入的特征ϕ的一次函数,并通过最小二乘直接计算一次函数的系数Rk和bk,大大减少了计算量。
相关文章推荐
- 人脸对齐SDM原理----Supervised Descent Method and its Applications to Face Alignment
- SDM(Supervised Descent Method)用于人脸对齐的C++实现方法
- 人脸对齐之SDM(Supervised Descent Method)
- 人脸对齐SDM原理----Supervised Descent Method and its Applications to Face Alignment
- SDM(superviseddescentmethod)人脸特征点训练
- 人脸对齐之SDM论文解析
- 【人脸对齐】Supervised Descent Method and its Applications to Face Alignment
- Win下 C++版SDM(Supervised Descent Method)算法实现
- SDM(Supervised Descent Method)算法的简单实现
- Supervised Descent Method and its Applications to Face Alignment(SDM)
- paper 142:SDM算法--Supervised Descent Method
- SDM(supervised descent method)算法
- Supervised Descent Method and its Applications to Face Alignment
- 【OpenCV】人脸对齐landmark及位置姿态EstimateHeadPose(SDM)
- Cmake+vs2013 配置生成source文件——superviseddescend method(SDM)
- SDM for face alignment 人脸对齐相关资料整理
- Supervised Descent Method and its Applications to Face Alignment
- SDM人脸对齐算法研究
- 人脸对齐SDM技术
- Supervised Descent Method 简单实现
