【动态规划】棋盘分割问题
2017-03-29 21:06
232 查看
描述
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差

,其中平均值
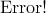
,xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
输入第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出仅一个数,为O'(四舍五入精确到小数点后三位)。
样例输入
样例输出
1.633
题意简介:
有一个8*8的棋盘,每次将当前的棋盘分成两半,然后选择一半继续分。
一共分n-1次。
问这n个棋盘的最小均方差是多少?
(n<15)
解题思路:
将棋盘分割时,会逐步分割其中二分之一(非均匀二分之一,两者中的其中一个),让我想到小学时玩的挣地盘划线游戏,不过此题中给出的一个n行n列的矩阵,并且每次划线是沿边线来划分的,并且是符合规则的划线,即一次划透。但结果是求的矩形棋盘面积的方差和。所以是动态规划问题的解决思路,求全局最小解,自顶向下。min(a
)=min(a[n-1],a
-k)类似的这种情况。
首先棋盘分割时分割完每个矩形块会有四个角,矩形可以通过左上角右下角坐标用来表示:dp(x1,y1,x2,y2);
dp(x1,y1,x2,y2);
面积为Si(i为1,2,3.....k(k-1次分割次数))
则所求为:平方->(Si-(S1+.....Si)/n) /n;
显然,由于块数是固定的n,平均数(x)等于所有数字的和除n。
那么我们只需求出每块的最小平方和即可,这个是很典型的DP:
可以列出状态方程:
map[k][x1][y1][x2][y2] = min{
map[0][x1][y1][t][y2]+map[k-1][t+1][y1][x2][y2], (x1 <= t < x2)
map[k-1][x1][y1][t][y2]+map[0][t+1][y1][x2][y2], (x1 <= t < x2) //竖切
map[0][x1][y1][x2][t]+map[k-1][x1][t+1][x2][y2], (y1 <= t < y2)
map[k-1][x1][y1][x2][t]+map[0][x1][t+1][x2][y2] (y1 <= t < y2) //横切
}
#include <iostream> #include <cstdio> #include <cmath> #include <iomanip> using namespace std; int data[9][9]; int sum[9][9]; double
map[14][9][9][9][9]; //返回左上角坐标(x1,y1)到右下角坐标(x2,y2)区域的棋盘的分值和平方 double count(int x1, int y1, int x2, int y2) { double ans = (double)(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]); return ans*ans; } int main() { int n, total=0; //输入数据 cin>>n; for(int
i=1; i<=8; ++i) for(int j=1; j<=8; ++j) { cin>>data[i][j]; //sum[i][j]表示棋盘(1,1)到(i,j)区域的累计分值 sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + data[i][j]; //total表示整个棋盘的分值之和 total += data[i][j]; } //初始化map数组 for(int x1=1; x1<=8; ++x1) for(int y1=1; y1<=8;
++y1) for(int x2=x1; x2<=8; ++x2) for(int y2=y1; y2<=8; ++y2) map[0][x1][y1][x2][y2] = count(x1,y1,x2,y2); //自底向上计算map数据 for(int k=1; k<n; ++k) for(int x1=1; x1<=8; ++x1) for(int y1=1; y1<=8; ++y1) for(int x2=x1; x2<=8; ++x2) for(int y2=y1; y2<=8; ++y2) {
int t; map[k][x1][y1][x2][y2] = (double)(1<<30); for(t=x1; t<x2; ++t) { map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[0][x1][y1][t][y2]+map[k-1][t+1][y1][x2][y2]); map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[k-1][x1][y1][t][y2]+map[0][t+1][y1][x2][y2]);
} for(t=y1; t<y2; ++t) { map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[0][x1][y1][x2][t]+map[k-1][x1][t+1][x2][y2]); map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[k-1][x1][y1][x2][t]+map[0][x1][t+1][x2][y2]); } } //计算方差平方 double ans =
map[n-1][1][1][8][8]*1.0/n - ((double)total*1.0/n)*((double)total*1.0/n); //输出方差,精确到小数点后三位 cout<<setprecision(3)<<fixed<<sqrt(ans); return 0; }
此图虽然可解但是从上题可看出当自底向上计算map值时,复杂度竟然高达n的五次方,虽然此题有限制在0~8之间复杂度常数项不算太高,但是假若将棋盘扩大到非常大时,时间复杂度太高.
然后就写了上图代码,发现递归照常时间复杂度高。和for循环复杂度差不多。
------------------------------------
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差

,其中平均值
,xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
输入第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出仅一个数,为O'(四舍五入精确到小数点后三位)。
样例输入
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
样例输出
1.633
题意简介:
有一个8*8的棋盘,每次将当前的棋盘分成两半,然后选择一半继续分。
一共分n-1次。
问这n个棋盘的最小均方差是多少?
(n<15)
解题思路:
将棋盘分割时,会逐步分割其中二分之一(非均匀二分之一,两者中的其中一个),让我想到小学时玩的挣地盘划线游戏,不过此题中给出的一个n行n列的矩阵,并且每次划线是沿边线来划分的,并且是符合规则的划线,即一次划透。但结果是求的矩形棋盘面积的方差和。所以是动态规划问题的解决思路,求全局最小解,自顶向下。min(a
)=min(a[n-1],a
-k)类似的这种情况。
首先棋盘分割时分割完每个矩形块会有四个角,矩形可以通过左上角右下角坐标用来表示:dp(x1,y1,x2,y2);
dp(x1,y1,x2,y2);
面积为Si(i为1,2,3.....k(k-1次分割次数))
则所求为:平方->(Si-(S1+.....Si)/n) /n;
显然,由于块数是固定的n,平均数(x)等于所有数字的和除n。
那么我们只需求出每块的最小平方和即可,这个是很典型的DP:
可以列出状态方程:
map[k][x1][y1][x2][y2] = min{
map[0][x1][y1][t][y2]+map[k-1][t+1][y1][x2][y2], (x1 <= t < x2)
map[k-1][x1][y1][t][y2]+map[0][t+1][y1][x2][y2], (x1 <= t < x2) //竖切
map[0][x1][y1][x2][t]+map[k-1][x1][t+1][x2][y2], (y1 <= t < y2)
map[k-1][x1][y1][x2][t]+map[0][x1][t+1][x2][y2] (y1 <= t < y2) //横切
}
#include <iostream>
#include <cstdio>
#include <cmath>
#include <iomanip>
using namespace std;
int data[9][9];
int sum[9][9];
double map[14][9][9][9][9];
//返回左上角坐标(x1,y1)到右下角坐标(x2,y2)区域的棋盘的分值和平方
double count(int x1, int y1, int x2, int y2)
{
double ans = (double)(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]);
return ans*ans;
}
int main()
{
int n, total=0;
//输入数据
cin>>n;
for(int i=1; i<=8; ++i)
for(int j=1; j<=8; ++j)
{
cin>>data[i][j];
//sum[i][j]表示棋盘(1,1)到(i,j)区域的累计分值
sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + data[i][j];
//total表示整个棋盘的分值之和
total += data[i][j];
}
//初始化map数组
for(int x1=1; x1<=8; ++x1)
for(int y1=1; y1<=8; ++y1)
for(int x2=x1; x2<=8; ++x2)
for(int y2=y1; y2<=8; ++y2)
map[0][x1][y1][x2][y2] = count(x1,y1,x2,y2);
//自底向上计算map数据
for(int k=1; k<n; ++k)
for(int x1=1; x1<=8; ++x1)
for(int y1=1; y1<=8; ++y1)
for(int x2=x1; x2<=8; ++x2)
for(int y2=y1; y2<=8; ++y2)
{
int t;
map[k][x1][y1][x2][y2] = (double)(1<<30);
for(t=x1; t<x2; ++t)
{
map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[0][x1][y1][t][y2]+map[k-1][t+1][y1][x2][y2]);
map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[k-1][x1][y1][t][y2]+map[0][t+1][y1][x2][y2]);
}
for(t=y1; t<y2; ++t)
{
map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[0][x1][y1][x2][t]+map[k-1][x1][t+1][x2][y2]);
map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[k-1][x1][y1][x2][t]+map[0][x1][t+1][x2][y2]);
}
}
//计算方差平方
double ans = map[n-1][1][1][8][8]*1.0/n - ((double)total*1.0/n)*((double)total*1.0/n);
//输出方差,精确到小数点后三位
cout<<setprecision(3)<<fixed<<sqrt(ans);
return 0;
}#include <iostream> #include <cstdio> #include <cmath> #include <iomanip> using namespace std; int data[9][9]; int sum[9][9]; double
map[14][9][9][9][9]; //返回左上角坐标(x1,y1)到右下角坐标(x2,y2)区域的棋盘的分值和平方 double count(int x1, int y1, int x2, int y2) { double ans = (double)(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]); return ans*ans; } int main() { int n, total=0; //输入数据 cin>>n; for(int
i=1; i<=8; ++i) for(int j=1; j<=8; ++j) { cin>>data[i][j]; //sum[i][j]表示棋盘(1,1)到(i,j)区域的累计分值 sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + data[i][j]; //total表示整个棋盘的分值之和 total += data[i][j]; } //初始化map数组 for(int x1=1; x1<=8; ++x1) for(int y1=1; y1<=8;
++y1) for(int x2=x1; x2<=8; ++x2) for(int y2=y1; y2<=8; ++y2) map[0][x1][y1][x2][y2] = count(x1,y1,x2,y2); //自底向上计算map数据 for(int k=1; k<n; ++k) for(int x1=1; x1<=8; ++x1) for(int y1=1; y1<=8; ++y1) for(int x2=x1; x2<=8; ++x2) for(int y2=y1; y2<=8; ++y2) {
int t; map[k][x1][y1][x2][y2] = (double)(1<<30); for(t=x1; t<x2; ++t) { map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[0][x1][y1][t][y2]+map[k-1][t+1][y1][x2][y2]); map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[k-1][x1][y1][t][y2]+map[0][t+1][y1][x2][y2]);
} for(t=y1; t<y2; ++t) { map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[0][x1][y1][x2][t]+map[k-1][x1][t+1][x2][y2]); map[k][x1][y1][x2][y2] = min(map[k][x1][y1][x2][y2], map[k-1][x1][y1][x2][t]+map[0][x1][t+1][x2][y2]); } } //计算方差平方 double ans =
map[n-1][1][1][8][8]*1.0/n - ((double)total*1.0/n)*((double)total*1.0/n); //输出方差,精确到小数点后三位 cout<<setprecision(3)<<fixed<<sqrt(ans); return 0; }
此图虽然可解但是从上题可看出当自底向上计算map值时,复杂度竟然高达n的五次方,虽然此题有限制在0~8之间复杂度常数项不算太高,但是假若将棋盘扩大到非常大时,时间复杂度太高.
#include<iostream>
#include<stdlib.h>
#include<string.h>
#include<cmath>
using namespace std;
int record[10][8][8][8][8];
int sum[9][9],a[9][9];
int Cal_(int x1,int y1,int x2,int y2);
int min(int x1,int x2);
int fun(int n,int x1,int y1,int x2,int y2)
{
int t,a,b,c,d,e,Min=10000;
if(record
[x1][y1][x2][y2]!=1)
return record
[x1][y1][x2][y2];
if(n==1)
{
t=Cal_(x1,y1,x2,y2);
record
[x1][y1][x2][y2]=t*t;
return t*t;
}
for(a=x1;a<x2;a++) //竖直划分
{
c=Cal_(a+1,y1,x2,y2);
e=Cal_(x1,y1,a,y2);
t=min(fun(n-1,x1,y1,a,y2)+c*c,fun(n-1,a+1,y1,x2,y2)+e*e);
if(Min>t) Min=t;
}
for(b=y1;b<y2;b++) //水平划分
{
c=Cal_(x1,b+1,x2,y2);
e=Cal_(x1,y1,x2,b);
t=min(fun(n-1,x1,y1,x2,b)+c*c,fun(n-1,x1,b+1,x2,y2)+e*e);
if(Min>t) Min=t;
}
record
[x1][y1][x2][y2]=Min;
return Min;
}
int Cal_(int x1,int y1,int x2,int y2)
{
return sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1];
}
int min(int x1,int x2)
{
if(x1>x2)
return x1;
else
return x2;
}
int main()
{
int i,j;
int n;
int asum=0;
memset(sum,0,sizeof(sum));
memset(record,-1,sizeof(record));
cin>>n;
for(i=0;i<8;i++)
for(j=0;j<8;j++)
{
cin>>a[i][j];
asum+=a[i][j];
sum[i][j]=sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + a[i][j];
}
double sun=n*fun(n,1,1,8,8)-sum[8][8]*sum[8][8];
cout<<sqrt(sun/(n*n));
return 0;
}然后就写了上图代码,发现递归照常时间复杂度高。和for循环复杂度差不多。
------------------------------------
相关文章推荐
- poj1191棋盘分割—典型动态规划
- 递归分治算法之棋盘分割问题(Java版本)
- 【动态规划+递归】:poj1191,棋盘分割
- OpenJudge百炼-1191-棋盘分割-C语言-动态规划
- 经典问题六.【二维的区间dp】棋盘分割 poj 1191
- [NOI 1999]棋盘分割(动态规划)
- 【递归 & 动态规划】POJ 1191 棋盘分割
- poj1321——棋盘问题——————【状态压缩、动态规划】
- 算法基础之python实现递归法中棋盘分割问题
- POJ-1191 棋盘分割 动态规划
- 九度OJ 1532 棋盘寻宝扩展 -- 动态规划【背包问题】
- poj1191-棋盘分割问题
- 动态规划 简单的分割问题的解决方案钢棒
- 用动态规划的自底向上方法解决钢材分割的问题。
- poj1191棋盘分割—典型动态规划
- poj 1191 棋盘分割 动态规划
- 经典递归问题--棋盘分割 POJ--1191
- POJ-1191-棋盘分割(动态规划)
- 棋盘分割 动态规划
- POJ-1191-棋盘分割(动态规划)
