SVM matlab 代码详解说明

x=[0 1 0 1 2 -1];y=[0 0 1 1 2 -1];z=[-1 1 1 -1 1 1];
%其中，（x,y）代表二维的数据点，z 表示相应点的类型属性。

data=[1,0;0,1;2,2;-1,-1;0,0;1,1];% (x,y)构成的数据点
groups=[1;1;1;1;-1;-1];%各个数据点的标签
figure;
subplot(2,2,1);
Struct1 = svmtrain(data,groups,'Kernel_Function','quadratic', 'showplot',true);%data数据，标签，核函数，训练
classes1=svmclassify(Struct1,data,'showplot',true);%data数据分类，并显示图形
title('二次核函数');
CorrectRate1=sum(groups==classes1)/6　　

subplot(2,2,2);
Struct2 = svmtrain(data,groups,'Kernel_Function','rbf', 'RBF_Sigma',0.41,'showplot',true);
classes2=svmclassify(Struct2,data,'showplot',true);
title('高斯径向基核函数(核宽0.41)');
CorrectRate2=sum(groups==classes2)/6
subplot(2,2,3);
Struct3 = svmtrain(data,groups,'Kernel_Function','polynomial', 'showplot',true);
classes3=svmclassify(Struct3,data,'showplot',true);
title('多项式核函数');
CorrectRate3=sum(groups==classes3)/6
subplot(2,2,4);
Struct4 = svmtrain(data,groups,'Kernel_Function','mlp', 'showplot',true);
classes4=svmclassify(Struct4,data,'showplot',true);
title('多层感知机核函数');
CorrectRate4=sum(groups==classes4)/6

　　

svmtrain代码分析：
if plotflag   %画出训练数据的点
[hAxis,hLines] = svmplotdata(training,groupIndex);
legend(hLines,cellstr(groupString));
endscaleData = [];
if autoScale   %训练数据标准化
scaleData.shift = - mean(training);
stdVals = std(training);
scaleData.scaleFactor = 1./stdVals;
% leave zero-variance data unscaled:
scaleData.scaleFactor(~isfinite(scaleData.scaleFactor)) = 1;% shift and scale columns of data matrix:
for c = 1:size(training, 2)
training(:,c) = scaleData.scaleFactor(c) * ...
(training(:,c) + scaleData.shift(c));
end
end

　　

if strcmpi(optimMethod, 'SMO')%选择最优化算法
else % QP and LS both need the kernel matrix:
%求解出超平面的参数 (w,b):     wX+b

　　 

if plotflag  %画出超平面在二维空间中的投影
hSV = svmplotsvs(hAxis,hLines,groupString,svm_struct);
svm_struct.FigureHandles = {hAxis,hLines,hSV};
end

　　

svmplotsvs.m文件

hSV = plot(sv(:,1),sv(:,2),'ko');%从训练数据中选出支持向量，加上圈标记出来lims = axis(hAxis);%获取子图的坐标空间
[X,Y] = meshgrid(linspace(lims(1),lims(2)),linspace(lims(3),lims(4)));%根据x和y的范围，切分成网格，默认100份
Xorig = X; Yorig = Y;% need to scale the mesh    将这些隔点标准化
if ~isempty(scaleData)
X = scaleData.scaleFactor(1) * (X + scaleData.shift(1));
Y = scaleData.scaleFactor(2) * (Y + scaleData.shift(2));
end[dummy, Z] = svmdecision([X(:),Y(:)],svm_struct); %计算这些隔点[标签，离超平面的距离]
contour(Xorig,Yorig,reshape(Z,size(X)),[0 0],'k');%画出等高线图，这个距离投影到二维空间的等高线

　　

svmdecision.m文件
function [out,f] = svmdecision(Xnew,svm_struct)
%SVMDECISION evaluates the SVM decision function%   Copyright 2004-2006 The MathWorks, Inc.
%   $Revision: 1.1.12.4 $  $Date: 2006/06/16 20:07:18 $sv = svm_struct.SupportVectors;
alphaHat = svm_struct.Alpha;
bias = svm_struct.Bias;
kfun = svm_struct.KernelFunction;
kfunargs = svm_struct.KernelFunctionArgs;f = (feval(kfun,sv,Xnew,kfunargs{:})'*alphaHat(:)) + bias;%计算出距离
out = sign(f);%距离转化成标签
% points on the boundary are assigned to class 1
out(out==0) = 1;

　　

function K = quadratic_kernel(u,v,varargin)%核函数计算
%QUADRATIC_KERNEL quadratic kernel for SVM functions% Copyright 2004-2008 The MathWorks, Inc.dotproduct = (u*v');
K = dotproduct.*(1 + dotproduct);

　　维度分析：假设输入的训练数据为m个，维度为d，记作X(m,d);显然w为w(m,1);    wT*x+b核函数计算:k(x,y)->上公式改写成  wT*@(x)+b假设支持的向量跟训练数据保持一致，没有筛选掉一个，则支撑的数据就是归一化后的X,记作：Xst;测试数据为T(n,d);则核函数计算后为：(m,d)*(n,d)'=m*n;与权重和偏移中以后为： (1,m)*(m*n)=1*n；如果是训练数据作核函数处理，则m*d变成为m*m这n个测试点的距离。将这些隔点和其对应的超平面距离，画成等高线，得到现有图形。  第二批测试数据：

clc;
clear;
close all;
%rng(1); % For reproducibility
r = sqrt(rand(100,1)); % Radius 0~1
t = 2*pi*rand(100,1); % Angle 0~2pi
data1 = [r.*cos(t), r.*sin(t)]; % Pointsr2 = sqrt(3*rand(100,1)+1); % Radius 1~4
t2 = 2*pi*rand(100,1); % Angle 0~2pi
data2 = [r2.*cos(t2), r2.*sin(t2)]; % pointsfigure;
plot(data1(:,1),data1(:,2),'r.','MarkerSize',15)
hold on
plot(data2(:,1),data2(:,2),'b.','MarkerSize',15)
ezpolar(@(x)1);ezpolar(@(x)2);
axis equal
hold off%Put the data in one matrix, and make a vector of classifications.
data3 = [data1;data2];%标签 +1 -1
theclass = ones(200,1);
theclass(1:100) = -1;

　　  

% r^2(r的平方) KMatrix = exp(-gamma*r2);
function KMatrix = getKRBF(X, Y, gamma)%rbf核函数
r2 =  repmat( sum(X.^2,2), 1, size(Y,1) ) ...
+ repmat( sum(Y.^2,2), 1, size(X,1) )'- 2*X*Y'
%K(x,y)     m*n
%sum(X.^2,2)   m*d  ->   m*1  ->   repmat ->  m*n
%              n*d  ->   n*1  ->   n*m    ->  m*n
%m*n% XVec表示X向量。||XVec||表示向量长度。 r表示两点距离。r^2表示r的平方。
% k(XVec,YVec) = exp(-1/(2*sigma^2)*(r^2)) = exp(-gamma*r^2)
% 公式-1 这里, gamma=1/(2*sigma^2)是参数, r=||XVec-YVec|| 实际上，可看作是计算2个点X与Y的相似性。

　　核函数理论：参考：http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html考虑我们最初在“线性回归”中提出的问题，特征是房子的面积x，这里的x是实数，结果y是房子的价格。假设我们从样本点的分布中看到x和y符合3次曲线，那么我们希望使用x的三次多项式来逼近这些样本点。那么首先需要将特征x扩展到三维

，然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射（feature
mapping）。映射函数称作

，在这个例子中

我们希望将得到的特征映射后的特征应用于SVM分类，而不是最初的特征。这样，我们需要将前面

公式中的内积从

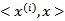
，映射到

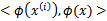
。至于为什么需要映射后的特征而不是最初的特征来参与计算，上面提到的（为了更好地拟合）是其中一个原因，另外的一个重要原因是样例可能存在线性不可分的情况，而将特征映射到高维空间后，往往就可分了。（在《数据挖掘导论》Pang-Ning Tan等人著的《支持向量机》那一章有个很好的例子说明）将核函数形式化定义，如果原始特征内积是

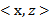
，映射后为

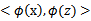
，那么定义核函数（Kernel）为

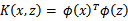
到这里，我们可以得出结论，如果要实现该节开头的效果，只需先计算

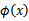
，然后计算

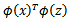
即可，然而这种计算方式是非常低效的。比如最初的特征是n维的，我们将其映射到

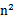
维，然后再计算，这样需要

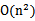
的时间。那么我们能不能想办法减少计算时间呢？先看一个例子，假设x和z都是n维的，

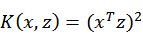
 展开后，得

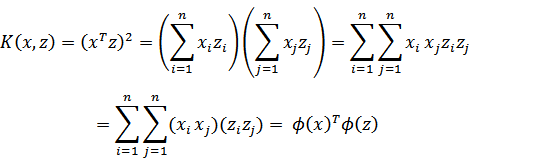
这个时候发现我们可以只计算原始特征x和z内积的平方（时间复杂度是O(n)），就等价与计算映射后特征的内积。也就是说我们不需要花

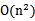
时间了。现在看一下映射函数（n=3时），根据上面的公式，得到

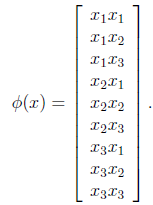
也就是说核函数

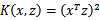
只能在选择这样的

作为映射函数时才能够等价于映射后特征的内积。再看一个核函数

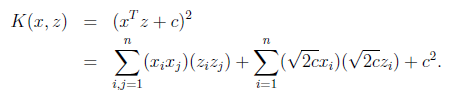
对应的映射函数（n=3时）是

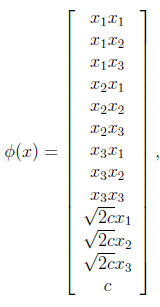
轮换对称更一般地，核函数

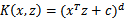
对应的映射后特征维度为

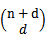
。（求解方法参见http://zhidao.baidu.com/question/16706714.html）。由于计算的是内积，我们可以想到IR中的余弦相似度，如果x和z向量夹角越小，那么核函数值越大，反之，越小。因此，核函数值是

和

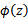
的相似度。再看另外一个核函数

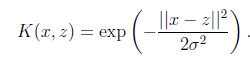
这时，如果x和z很相近（

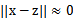
），那么核函数值为1，如果x和z相差很大（

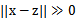
），那么核函数值约等于0。由于这个函数类似于高斯分布，因此称为高斯核函数，也叫做径向基函数(Radial
Basis Function 简称RBF)。它能够把原始特征映射到无穷维。既然高斯核函数能够比较x和z的相似度，并映射到0到1，回想logistic回归，sigmoid函数可以，因此还有sigmoid核函数等等。下面有张图说明在低维线性不可分时，映射到高维后就可分了，使用高斯核函数。

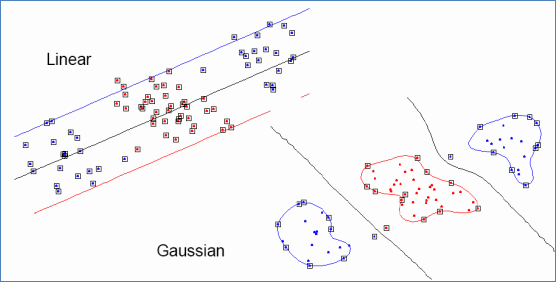
来自Eric Xing的slides注意，使用核函数后，怎么分类新来的样本呢？线性的时候我们使用SVM学习出w和b，新来样本x的话，我们使用

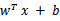
来判断，如果值大于等于1，那么是正类，小于等于是负类。在两者之间，认为无法确定。如果使用了核函数后，

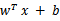
就变成了

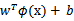
，是否先要找到

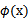
，然后再预测？答案肯定不是了，找

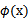
很麻烦，回想我们之前说过的

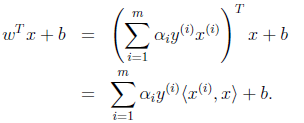
只需将

替换成

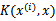
，然后值的判断同上。核函数不仅仅用在SVM上，但凡在一个模型后算法中出现了

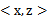
，我们都可以常使用

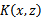
去替换，这可能能够很好地改善我们的算法。  参考：http://blog.csdn.net/shijing_0214/article/details/51000845由之前对核函数的定义（见统计学习方法定义7.6）： 设χ是输入空间（欧氏空间或离散集合），Η为特征空间（希尔伯特空间），如果存在一个从χ到Η的映射 φ(x): χ→Η使得对所有的x,z∈χ,函数Κ(x,z)=φ(x)∙φ(z)， 则称Κ(x,z)为核函数，φ(x)为映射函数，φ(x)∙φ(z)为x,z映射到特征空间上的内积。 由于映射函数十分复杂难以计算，在实际中，通常都是使用核函数来求解内积，计算复杂度并没有增加，映射函数仅仅作为一种逻辑映射，表征着输入空间到特征空间的映射关系。例如： 设输入空间χ：

, 映射函数φ(x)= < X,X > =

 核函数Κ(x,z)=

 那么，取两个样例x=(1,2,3),z=(4,5,6)分别通过映射函数和核函数计算内积过程如下： φ(x)=(1,2,3,2,4,6,3,6,9) φ(z)=(16,20,24,20,25,30,24,30,36) φ(x)∙φ(z)=16+40+72+40+100+180+72+180+324=1024 而直接通过Κ(x,z)计算得[(4+10+18)]^2=1024 两者相比，核函数的计算量显然要比映射函数小太多了。