RSA非对称加密算法详解

加密概要

加密技术是对信息进行编码和解码的技术，编码是把原来可读信息（又称明文）译成代码形式（又称密文），其逆过程就是解码（解密），加密技术的要点是加密算法，加密算法可以分为三类：

1. 对称加密

2. 非对称加密

3. 不可逆加密

对称加密算法

加密过程：

将明文分成N个组，然后对各个组进行加密，形成各自的密文，最后把所有的分组密文进行合并，形成最终的密文。

优点：

算法公开、计算量小、加密速度快、加密效率高

缺点：

交易双方都使用同样钥匙，安全性得不到保证

密钥管理困难，尤其是在分布式网络中

常用算法：

DES、3DES（TripleDES）、AES、RC2、RC4、RC5和Blowfish

非对称加密算法

使用过程：

乙方生成两把密钥（公钥和私钥）

甲方获取乙方的公钥，然后用它对信息加密。

乙方得到加密后的信息，用私钥解密，乙方也可用私钥加密字符串

甲方获取乙方私钥加密数据，用公钥解密

优点：

更安全，密钥越长，它就越难破解

缺点：

加密速度慢

常用算法：

RSA、Elgamal、背包算法、Rabin、D-H、ECC（椭圆曲线加密算法)

RSA算法历史

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名

数论基础

1. 欧拉函数

定义：对于一个正整数 n ，小于 n 且和 n 互质的正整数（包括 1）的个数，记作 φ(n).则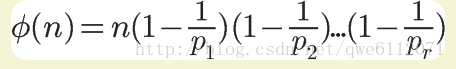



证明：

如果n是一个质数，那么

φ(n) = n-1

如果n是一个质数p的幂，即

n = p^k

，则

φ(n) = p^k-p^(k-1) = (p-1)*p^(k-1)

欧拉函数是一个积性函数，当n,m互质的时候，

φ(n*m) = φ(n)*φ(m)

2. 欧拉定理

定义：如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：a^φ(n)%n=1

证明：

3. 费马小定理

定义：假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成：a^(p-1)%n=1

4. 模反元素（乘积逆元）

定义：两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1：a*b%n=1,这时，b就叫做a的”模反元素”。

比如，3和11互质，那么3的模反元素就是4，因为 (3 * 4)-1 可以被11整除。4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素

模反元素必定存在，因为：

a^φ(n)=a*a^(φ(n)-1)

RSA算法实现步骤

原理：将两个大素数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥

下面是产生非对称密钥的算法流程



下面是加解密的算法流程



RSA算法可靠性分析

算法涉及到的参量：p、q、n、Φ(n)、e、d，而d泄露->私钥被破解，问题：能否在已知n和e的情况下，推导出d？

破解步骤：

ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。

φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。

n=pq。只有将n因数分解，才能算出p和q。

需要将因式分解n，当n位数达到1024，破解极为困难

RSA核心算法

快速幂取模算法

算法1：连乘算法，时间复杂度O(n)

算法2：快速幂算法，时间复杂度O(logn)

def myPow(self, x, n):
def rec_pow(x,n):
if n == 0:
return 1
elif n == 1:
return x
return rec_pow(x*x,n / 2) * rec_pow(x,n&1)
if n >= 0:
return rec_pow(x,n)
else:
return 1/rec_pow(x,-n)

算法3：快速幂取模算法，时间复杂度O(logn)

def superPow(self, a, b,m):
def myPow(a,b):
if b == 0:
return 1
a = a%m
if b == 1:
return a
return myPow(a*a,b/2) * myPow(a,b&1) % m
res = myPow(a,b)
return res

素数判定算法

算法1：试除法，错误率=0,时间复杂度o(n)，当数特别大时，算法速度慢

算法2：费马小定理

出错分析：

若基于2为底,对于512位大数，出错率为1/1020

卡米歇尔(Carmichael)数:它是合数, 当 1<=a<=n, 都有 a^n 三 a(mod n),255/100,000,000

卡米歇尔数的考塞特判别法: 设n是合数，则n是卡米歇尔数当且仅当它是奇数，且整除n的每个素数p满足下述两个条件:

p^2 不整除 n

p-1 整除 n-1

算法3：米勒拉宾素数测试

随机选取多组基数

改进：如果p是一个奇素数，方程x2≡1(mod p)仅仅有-1、1两个平凡解

速度快，而且可以判断

<2^63

的数

合数的拉宾-米勒测试定理: 设n是奇素数, 记

n-1 = 2^k * q

, q 是奇数, 对不被n整除的某个a, 如果下述两个条件都成立，则n是合数.

a^q !三 1（mod n)

;

对所有 i = 0, 1, 2, …., k-1,

a^((2^i)*q) !三 -1(mod n)

;

根据以上定理，可设计如下素数判定算法：

## 以一定概率判断是否为素数
def primeTest(n):
q = n - 1
k = 0
#Find k, q, satisfied 2^k * q = n - 1
while q % 2 == 0:
k += 1;
q /= 2
a = random.randint(2, n-2);
#If a^q mod n= 1, n maybe is a prime number
if fastExpMod(a, q, n) == 1:
return True
#If there exists j satisfy a ^ ((2 ^ j) * q) mod n == n-1,
#n maybe is a prime number
for j in range(0, k):
if fastExpMod(a, (2**j)*q, n) == n - 1:
return True
#a is not a prime number
return False
#多次测试，知道获取基本不可能为素数的“奇数”
def findPrime(halfkeyLength):
while True:
#Select a random number n
n = random.randint(0, 1<<halfkeyLength)
if n % 2 != 0:
found = True
#If n satisfy primeTest 10 times, then n should be a prime number
for _ in range(0, 10):
if not primeTest(n):
found = False
break
if found:
return n

拓展欧几里德算法

欧几里德算法(辗转相除法)

a=bq1+r1

b=rq2+r2

r1=r2q3+r3

……

rk-2=rk-1qk+rk

rk = 0,rk-1=gcd(a,b)

如gcd(20,7)=gcd(7,6)=gcd(1,0)

def gcd(a,b):
if not b:
return a
return gcd(b,a%b)

拓展的欧几里得算法:ax+by=rk-1=gcd(a,b)，求一组x,y

求逆元d:ed mod （p-1)*(q-1) = 1 =>

设 m = （p-1)*(q-1)，则mk+ed=1=gcd(m,e)

求满足条件的一组解k,d，最后取d

def ex_gcd(a,b):
global x,y
x,y = 1,0
def ex_gcd2(a,b):
global x,y
if b == 0:
return a
t = ex_gcd2(b, a%b)
x,y = y,x-(a/b)*y
return t
return ex_gcd2(a,b),x,y

RSA实际应用

SSH安全验证

级别一：基于口令

/etc/ssh/ssh_known_hosts

级别二：基于公钥(安全通信)

~/.ssh/id_rsa.pub

~/.ssh/id_rsa

~/.ssh/authorized_keys

下面是两种连接的示意流程图：



RSA应用——加密与认证的区别？

加密：公钥用于【加密】， 私钥用于【解密】

认证：公钥用于【解密】，私钥用于【加密】

数字签名&https原理

摘要算法（Hash算法、散列算法）

特性：

长度固定

CRC32 32比特（4字节）

MD5 128比特（16字节）

SHA1 160比特（20字节）

不可逆性

确定性

应用：完整性校验

校验文件是否缺失、被破坏、被修改

数字证书

具体内容

证书的发布机构

证书的有效期

公钥，证书所有者的公钥

证书所有者（Subject）

签名所使用的算法

指纹以及指纹算法，用于校验证书合法性

数字证书可以保证数字证书里的公钥确实是这个证书的所有者

改进的ssh连接（服务器身份认证部分）



https认证原理