统计学习精要(The Elements of Statistical Learning)课堂笔记（二十五）：降维和PCA

降维

降维完全属于unsupervised learning了，即给定数据集{x1,...,xn},xi∈Rp

，我们希望降到q维的{z1,...,zn}
。从这个角度来讲，降维和聚类还是有相通之处的，都是对于特征的提取。只是一个从行的角度出发，一个对列操作的感觉。

PCA（主成分分析，Principle Component Analysis）

个人觉得这也是起名字起的比较好的模型之一...乍一听起来很有用的感觉 -_-||
1. 求u1

,∥u1∥=1使得zi=uixi，且∑z2i
最大。





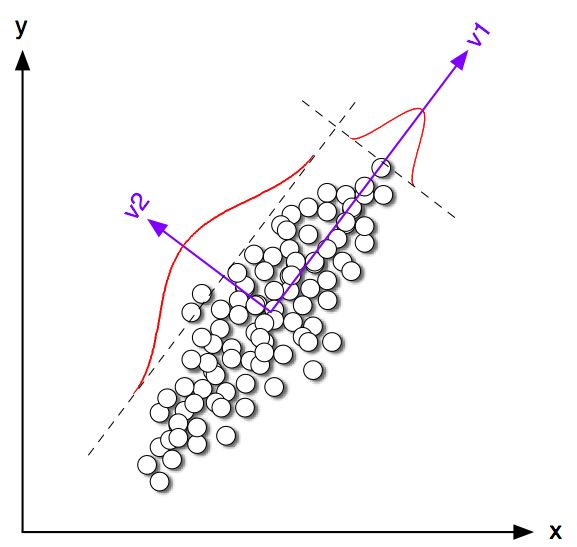
直觉上来讲，就是想寻找一个主方向。

这样，求解问题为：

max∑z2i=∑(u1xi)2=∑u′1xix′iu1=u′1(∑xix′i)u1

。所以我们只需要求一阶导数∂∑z2i∂u1
即可。

设A为对称矩阵，则存在正交阵u′u=I

使得A=uΛu′，其中Λ=⎡⎣⎢⎢λ1⋱�λn⎤⎦⎥⎥为A的特征值矩阵，故Aui=λiui(列向量为特征向量）。不失一般性，我们可以排序使得λ1≥λ2≥...≥λn
（从大到小排序）。

最大特征值:
max∥x∥=1x′Ax=λ1

同时C=1n∑xix′i

为x的相关矩阵，{u1,u2,...,uq}=Uq，从而zi=UqU′qxi,∀i
2. 找到{u1,u2,...,uq}=Uq

(q维的子空间）

将xi

投影到该q维空间，这样zi=UqU′qxi=Uq⎡⎣⎢⎢u′1⋮u′q⎤⎦⎥⎥xi=Uq⎡⎣⎢⎢u′1xi⋮u′qxi⎤⎦⎥⎥=[u1,u2,...,uq]⎡⎣⎢⎢u′1xi⋮u′qxi⎤⎦⎥⎥=(u′1xi)u1+...+(u′qxi)uq，且∥uqu′qx−x∥2F
最小。

A矩阵的范数：∥A∥F=∑i∑ja2ij=tr(AA′)

tr表示矩阵的迹（对角线元素和）。

则上述问题等价于，求(u1,...,uq)=Uq

使得tr[(uqu′qx−x)′(uqu′qx−x)]
最小。

=tr(x′UqU′qUqU′qx−x′UqU′qx−x′UqU′qx+x′x)=tr(−x′UqU′qx+x′x)

最小。

即使得tr(x′UqU′qx)

最大（注意没有负号）。

S=x′x

称为数据的相似矩阵=(x′ixj)
。

AA′

和A′A均为对称阵，且两个阵有相同的特征值。记r为A的秩，AA'的特征向量u1,...,um∈Rm，A'A的特征向量v1,...,vm∈Rn，则A′ui=λiui，A′vi=λivi。做奇异值分解，则A=UΛV′
.

由此，tr(x′UqU′qx)

求得的和前述结果等价。

回到PCA。如果降维后需要重构，则uizi=xi^

，解min∑i∥xi−xi^∥
即可。

3. 对偶PCA。如果p≥n

即数据非常高的时候，可以转置后再做。

4. KPCA （kernel）PCA也可以先用核函数Φ(⋅)

，即实现非线性的降维。需要注意，降维的过程需要保持可逆。

---------------
PS. PCA不适合解决overfitting的问题。如果需要解决，加regularization项。