统计机器学习笔记——EM算法及其应用(1)

EM算法的适用场景：

EM算法用于估计含有隐变量的概率模型参数的极大似然估计，或者极大后验概率估计。当概率模型既含有观测值，又含有隐变量或潜在变量时，就可以使用EM算法来求解概率模型的参数。当概率模型只含有观测值时，直接使用极大似然估计法，或者贝叶斯估计法估计模型参数就可以了。

EM算法的入门简单例子：

已知有三枚硬币A，B，C，假设抛掷A，B，C出现正面的概率分别为π ，p ，q 。

单次实验的过程是:

首先抛掷硬币A，如果A出现正面选择硬币B，否则，选择硬币C。

抛掷所选择的硬币，正面输出1，反面输出0。

重复上述单词实验n次，需要估计抛掷硬币A，B，C出现正面的概率π ，p ，q 。其中每次实验步骤1的抛掷结果不可见，可见的是所挑选硬币的抛掷结果。



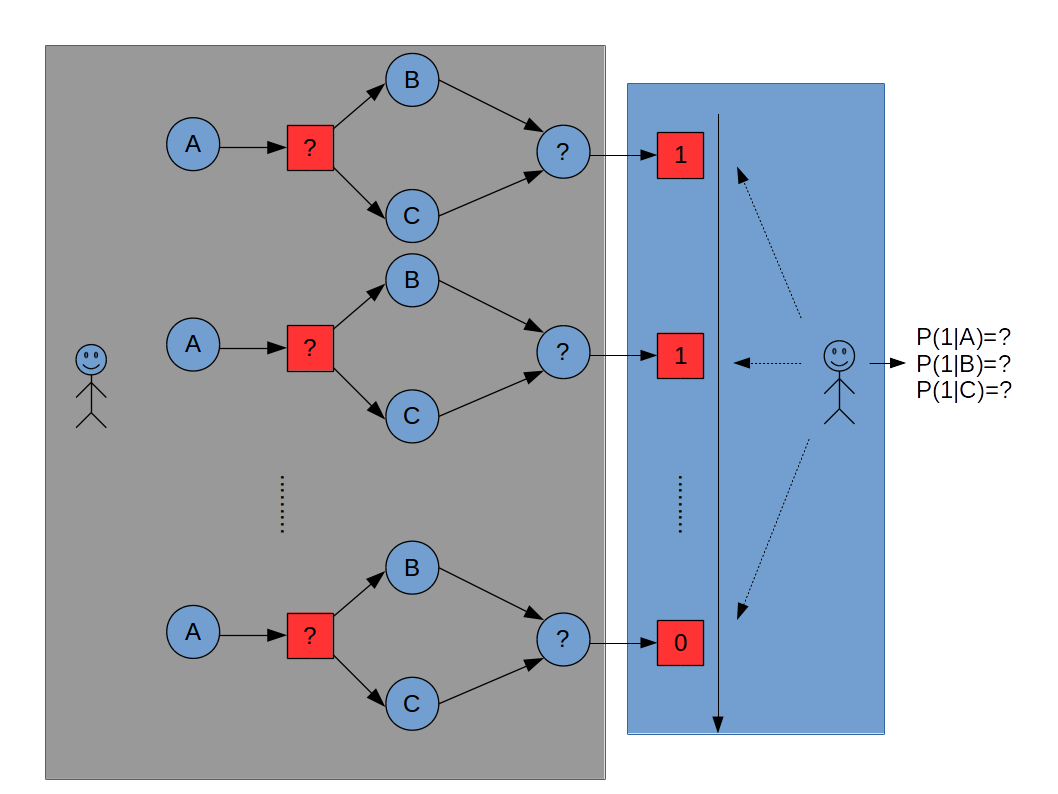
解：

P(y|θ)=∑ z P(y,z|θ)=∑ z P(z|θ)P(y|z,θ)

注：

θ 表示的是整个模型的参数，也就是我们学习的目标。

y 是二元随机变量(取值为0或者1,也可以对应于C或者B)，为观测随机变量。

z 是二元随机变量(取值为0或者1,也可以对应于C或者B), 为隐变量（不可观测）

根据全概率公式可得P(y|θ)=∑ z P(y,z|θ)

而求和中的每一项根据条件概率公式得P(y,z|θ)=P(z|θ)P(y|z,θ)

θ=(π,p,q)

P(y|θ)=πp y (1−p) 1−y +(1−π)q y (1−q) 1−y

也可做如下理解：

P(y|θ)=P(y,B|θ)+P(y,C|θ)=P(C|θ)P(y|C,θ)+P(B|θ)P(y|B,θ)

P(y|θ)=(1−π)P(y|C,θ)+πP(y|B,θ)

P(y|θ)=(1−π)q y (1−q) 1−y +πp y (1−q) 1−y

设Z=(Z 1 ,Z 2 ,⋯,Z n ) 为n次实验的隐状态（不可观测）序列，Y=(Y 1 ,Y 2 ,⋯,Y n ) 为n次实验的观测序列

那么每次实验对应观测值的概率为：P(Y i |θ)=∑ Z P(Z|θ)P(Y|Z,θ)

这个观测序列的概率为P(Y|θ)=∏ i=1 n P(Y i |θ)=∏ i=1 n {πp y (1−p) 1−y +(1−π)q y (1−q) 1−y }

那么我们的学习目标就是让P(Y|θ) 出现的概率近可能的大，即θ ^ =argmax θ logP(Y|θ)

这个问题没有解析解（未知量的个数大于样本数，多出来一些隐变量），只能通过迭代的方法求解。EM算法就是用来解决这类问题的。

求解步骤如下：

初始化参数θ (0)

然后通过下面的步骤计算参数的估计值,直至收敛:

2.1 E步骤（对隐变量进行估计,是在每个观测值上都要计算的）：计算在参数π (i) , p (i) , q (i) 下观测数据y j 来自投掷硬币B的概率：

P(B|y j ,θ)=P(B,y j |θ)P(y j |θ)

P(y j |θ)=P(y j ,B|theta)+P(y j ,C|theta)

P(y j |θ)=π (i) (p (i) ) y j (1−p (i) ) (1−y j ) +(1−π (i) )(q (i) ) y j (1−q (i) ) (1−y j )

P(B,y j |θ)=P(B|θ)P(y j |θ)

P(B,y j |θ)=π (i) (p (i) ) y j (1−p (i) ) (1−y j )

P(B|y j ,θ)=π (i) (p (i) ) y j (1−p (i) ) (1−y j ) π (i) (p (i) ) y j (1−p (i) ) (1−y j ) +(1−π (i) )(q (i) ) y j (1−q (i) ) (1−y j ) =μ (i+1) j

2.2 M步骤（是在每个观测值计算E后进行的）：更新模型的权重参数

P(B j |θ)=π j =1n ∑ j=1 n P(B j |y j ,θ)

π (i+1) =1n ∑ j=1 n P(B j |y j ,θ) (i+1) =1n ∑ j=1 n μ (i+1) j

P(y j =1|B j ,θ)=p j =P(y j =1,B j |θ)P(B j |θ)

p (i+1) =∑ j=1 n μ (i+1) j y j ∑ j=1 n μ (i+1) j

P(y j =1|C j ,θ)=q j =P(y j =1,C j |θ)P(C j |θ) =P(y j =1,C j |θ)P(C j |θ)

p (i+1) =∑ j=1 n (1−μ (i+1) j )y j ∑ j=1 n (1−μ (i+1) j )

使用具体数值进行运算：

设初值为：π (0) =0.5 ，p (0) =0.5 ，q (0) =0.5 ，观测序列为1，1，0，1，0，0，1，0，1，1

μ (1) =0.5

π (1) =0.5 ，p (1) =0.6 ，q (1) =0.6

继续迭代，得π (2) =0.5 ，p (2) =0.6 ，q (2) =0.6

于是最终的模型参数θ 的极大似然估计：π ^ =0.5 ，p ^ =0.6 ，q ^ =0.6

当换一组初始化权重参数：

设初值为：π (0) =0.4 ，p (0) =0.6 ，q (0) =0.7 ，观测序列为1，1，0，1，0，0，1，0，1，1

于是最终的模型参数θ 的极大似然估计：π ^ =0.4064 ，p ^ =0.5368 ，q ^ =0.6432

对应的程序代码为：

import numpy as np

def generate_observe_sequence(n):
return (np.random.random(size=n)> 0.35).astype(np.int)

def Estep(observe_list, theta):

def sample_mu(y):
up_1 = theta[0] * np.power(theta[1], y) * np.power((1-theta[1]),(1-y))
up_2 = (1-theta[0]) * np.power(theta[2], y) * np.power((1-theta[2]),(1-y))
return up_1/(up_1 + up_2)

return [sample_mu(y) for y in observe_list]

def MStep(observe_list, mus):
p = [0.0, 0.0, 0.0]
p[0] = sum(mus)/len(mus)
p[1] = sum([mus[i] * observe_list[i] for i in range(len(observe_list))])/sum(mus)
p[2] = sum([(1-mus[i]) * observe_list[i] for i in range(len(observe_list))])/sum([1-mu for mu in mus])
return p[:]

if __name__ == "__main__":
records = []
theta = [0.4, 0.6, 0.7]
m = 1e-7
records.append(theta)
observe_list = [1,1,0,1,0,0,1,0,1,1]
#observe_list = generate_observe_sequence(5)
print theta
while True:
mus = Estep(observe_list, theta)
new_theta = MStep(observe_list, mus)
print new_theta
records.append(new_theta)
err = 0
for old, new in zip(theta, new_theta):
err += np.abs(old-new)
print err
if err < m:
break
theta = new_theta[:]
print "###########################"
for record in records:
print record

通过上面的例子可以发现，EM算法受初值影响明显。

参考书目：《统计机器学习》李航