hihocoder1394网络流三之最小路径覆盖
2016-11-06 18:48
232 查看
题目连接:
一定要见双向边,第二次了…………………………。因为这两边的点是一样的
题目:
国庆期间正是旅游和游玩的高峰期。
小Hi和小Ho的学习小组为了研究课题,决定趁此机会派出若干个调查团去沿途查看一下H市内各个景点的游客情况。
H市一共有N个旅游景点(编号1..N),由M条单向游览路线连接。在一个景点游览完后,可以顺着游览线路前往下一个景点。
为了避免游客重复游览同一个景点,游览线路保证是没有环路的。
每一个调查团可以从任意一个景点出发,沿着计划好的游览线路依次调查,到达终点后再返回。每个景点只会有一个调查团经过,不会重复调查。
举个例子:
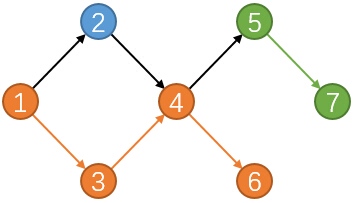
上图中一共派出了3个调查团:
1. 蓝色:调查景点;2
2. 橙色:调查景点;1->3->4->6
3. 绿色:调查景点;5->7
当然对于这个图还有其他的规划方式,但是最少也需要3个调查团。
由于小组内的人数有限,所以大家希望调查团的数量尽可能少,同时也要将所有的景点都进行调查。
当然,如何规划调查团线路的任务落到了小Hi和小Ho的头上。
提示:最小路径覆盖
第1行:2个整数N,M。1≤N≤500,0≤M≤20,000。
第2..M+1行:2个数字u,v,表示一条有向边(u,v)。保证不会出现重复的边,且不存在环。
第1行:1个整数,表示最少需要的调查团数量。
样例输入
样例输出
解法:
小Ho:所以这一次我们应该如何来解决这个问题呢?
小Hi:嗯,这次的问题被称为最小路径覆盖。给定一个有向无环图,用最少的路径数量去保证所有点都被覆盖住。
小Ho:既然有名字,那一定有固定的解法了?
小Hi:没错,最小路径覆盖的结果等于N-最大二分匹配。
小Ho:二分匹配?这和二分匹配有什么关系?给定的有向图不一定是二分图吧。
小Hi:当然不是在原图上进行的二分匹配了。我们需要对原图进行转化,同时这一次我们还要学习如何用网络流去解决二分匹配的问题。
小Ho:好,你快给我讲讲。
小Hi:好的好的,你别急。我们先从例子来分析:

在这个例子中,我们选择的三条路径都被染上了颜色。你有发现什么特殊之处么?
小Ho:嗯...<小Ho思考了一小会儿>...并没有什么特别的地方啊?
小Hi:把黑色的边去掉,你再看看呢?主要注意的是每个点的出入度数量。
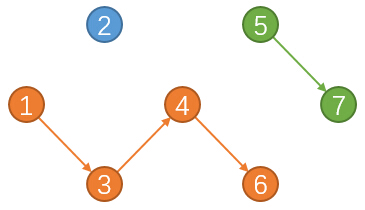
小Ho:对于一条路径,起点的入度为0,终点的出度为0,中间节点的出入度都为1。但这不是路径都应该具有的性质么?
小Hi:这个性质就是我们解决题目的关键!
每一个点最多只能有1个后继,同时每一个点最多只能有1个前驱。
假如我们选择了一条边(u,v),也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。
小Ho:那就是一个前驱匹配一个后继?
小Hi:是的,利用这个我们可以这样来构图:
将每一个点拆分成2个,分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部,所有后继节点作为B部。
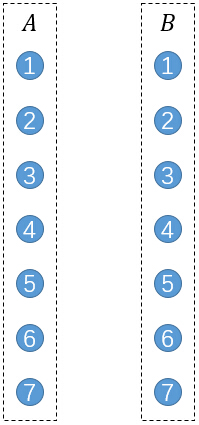
接下来进行连边,若原图中存在一条边(u,v),则连接A部的u和B部的v。
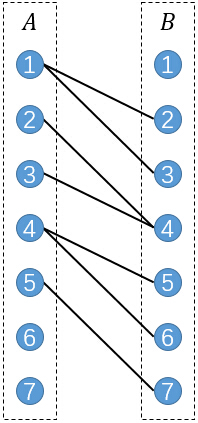
那么小Ho,你在这个上面做一个最大二分匹配怎么样?
小Ho:好!......完成了。
小Hi:不错,让我再把对应的颜色染出来:
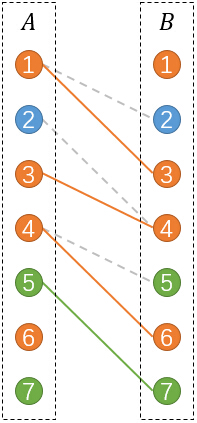
其中实线表示被选中的匹配,虚线表示未被选中的。
有没有发现,和原图刚好有着对应的关系。未被选中的匹配也正好对应了原图中我们没有选择的黑色边。
小Ho:是的呢?这是为什么呢?
小Hi:其实原理很简单。我们进行的匹配是前驱和后继的匹配。假如存在选中的匹配(i,j)和(j,k)。则表示原图中存在一条路径(i,j,k)。
比如例子中的匹配(1,3),(3,4),(4,6)就对应了原图中的路径(1,3,4,6)。
这样在匹配结束的时候,我们就可以直接通过匹配的情况来确定选中的路径。
小Ho:这个我懂了,但是如何保证这样就能得到最小的路径覆盖呢?
小Hi:你想想,每一条路径起点有什么特殊的地方?
小Ho:路径的起点入度为0...哦!我知道了。
如果一个点是路径起点的话,它在B部的节点一定是没有匹配上的。
经过最大匹配算法后,B部剩下没有被匹配的点一定是最少的,也就对应了最小需要的路径数。
所以最小路径覆盖的结果才是N-最大匹配数。
小Hi:正是这样,这样问题也就解决了。接下来第二个问题,怎么用网络流来解决二分匹配呢?
小Ho:上一次我们讲了二分多重匹配,二分匹配不就是它的简化版么。
只需要把源点s到A部的边和B部到汇点t的边容量限定为1就可以了!
小Hi:嗯,那么就只差最后一步了。
小Ho:这我也知道!实现嘛,交给我
代码:
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <stdlib.h>
#include <iomanip>
#include <fstream>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define maxn 1010
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define mem(a , b) memset(a , b , sizeof(a))
#define LL long long
#define ULL unsigned long long
#define FOR(i , n) for(int i = 1 ; i<= n ; i ++)
typedef pair<int , int> pii;
int n , m , ed;
vector<int>v[maxn];
int vis[maxn] , path[maxn] , a[maxn][maxn];
int flow[maxn] , ans;
bool BFS()
{
mem(vis , 0);
mem(path , -1);
mem(flow , 0);
queue<int>q;
while(!q.empty()) q.pop();
q.push(0);
vis[0] = 1;
flow[0] = INF;
while(!q.empty())
{
int cur = q.front();
q.pop();
if(cur == ed) return 1;
for(int i = 0 ; i < v[cur].size() ; i ++)
{
if(!vis[v[cur][i]] && a[cur][v[cur][i]] > 0)
{
vis[v[cur][i]] = 1;
flow[v[cur][i]] = min(flow[cur] , a[cur][v[cur][i]]);
path[v[cur][i]] = cur;
q.push(v[cur][i]);
}
}
}
return 0;
}
int main()
{
while(scanf("%d %d" , &n , &m) != EOF)
{
int s , to;
mem(a , 0);
ed = n + n + 1;
for(int i = 0 ; i < m ; i ++)
{
scanf("%d %d" , &s , &to);
v[s].push_back(to + n);
v[to+n].push_back(s);
a[s][to+n] = 1;
}
for(int i = 1 ; i <= n ; i ++)
{
v[0].push_back(i);
v[i].push_back(0);
a[0][i] = 1;
v[i+n].push_back(ed);
v[ed].push_back(i+n);
a[i+n][ed] = 1;
}
ans = 0;
while(BFS())
{
ans += flow[ed];
int fir = ed , sec = path[fir];
while(sec != -1)
{
a[fir][sec] += flow[ed];
a[sec][fir] -= flow[ed];
fir = sec;
sec = path[fir];
}
}
printf("%d\n" , n - ans);
}
return 0;
}
一定要见双向边,第二次了…………………………。因为这两边的点是一样的
题目:
描述
国庆期间正是旅游和游玩的高峰期。小Hi和小Ho的学习小组为了研究课题,决定趁此机会派出若干个调查团去沿途查看一下H市内各个景点的游客情况。
H市一共有N个旅游景点(编号1..N),由M条单向游览路线连接。在一个景点游览完后,可以顺着游览线路前往下一个景点。
为了避免游客重复游览同一个景点,游览线路保证是没有环路的。
每一个调查团可以从任意一个景点出发,沿着计划好的游览线路依次调查,到达终点后再返回。每个景点只会有一个调查团经过,不会重复调查。
举个例子:

上图中一共派出了3个调查团:
1. 蓝色:调查景点;2
2. 橙色:调查景点;1->3->4->6
3. 绿色:调查景点;5->7
当然对于这个图还有其他的规划方式,但是最少也需要3个调查团。
由于小组内的人数有限,所以大家希望调查团的数量尽可能少,同时也要将所有的景点都进行调查。
当然,如何规划调查团线路的任务落到了小Hi和小Ho的头上。
提示:最小路径覆盖
输入
第1行:2个整数N,M。1≤N≤500,0≤M≤20,000。第2..M+1行:2个数字u,v,表示一条有向边(u,v)。保证不会出现重复的边,且不存在环。
输出
第1行:1个整数,表示最少需要的调查团数量。样例输入
7 7 1 2 1 3 2 4 3 4 4 5 4 6 5 7
样例输出
3
解法:
小Ho:所以这一次我们应该如何来解决这个问题呢?
小Hi:嗯,这次的问题被称为最小路径覆盖。给定一个有向无环图,用最少的路径数量去保证所有点都被覆盖住。
小Ho:既然有名字,那一定有固定的解法了?
小Hi:没错,最小路径覆盖的结果等于N-最大二分匹配。
小Ho:二分匹配?这和二分匹配有什么关系?给定的有向图不一定是二分图吧。
小Hi:当然不是在原图上进行的二分匹配了。我们需要对原图进行转化,同时这一次我们还要学习如何用网络流去解决二分匹配的问题。
小Ho:好,你快给我讲讲。
小Hi:好的好的,你别急。我们先从例子来分析:

在这个例子中,我们选择的三条路径都被染上了颜色。你有发现什么特殊之处么?
小Ho:嗯...<小Ho思考了一小会儿>...并没有什么特别的地方啊?
小Hi:把黑色的边去掉,你再看看呢?主要注意的是每个点的出入度数量。

小Ho:对于一条路径,起点的入度为0,终点的出度为0,中间节点的出入度都为1。但这不是路径都应该具有的性质么?
小Hi:这个性质就是我们解决题目的关键!
每一个点最多只能有1个后继,同时每一个点最多只能有1个前驱。
假如我们选择了一条边(u,v),也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。
小Ho:那就是一个前驱匹配一个后继?
小Hi:是的,利用这个我们可以这样来构图:
将每一个点拆分成2个,分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部,所有后继节点作为B部。

接下来进行连边,若原图中存在一条边(u,v),则连接A部的u和B部的v。

那么小Ho,你在这个上面做一个最大二分匹配怎么样?
小Ho:好!......完成了。
小Hi:不错,让我再把对应的颜色染出来:

其中实线表示被选中的匹配,虚线表示未被选中的。
有没有发现,和原图刚好有着对应的关系。未被选中的匹配也正好对应了原图中我们没有选择的黑色边。
小Ho:是的呢?这是为什么呢?
小Hi:其实原理很简单。我们进行的匹配是前驱和后继的匹配。假如存在选中的匹配(i,j)和(j,k)。则表示原图中存在一条路径(i,j,k)。
比如例子中的匹配(1,3),(3,4),(4,6)就对应了原图中的路径(1,3,4,6)。
这样在匹配结束的时候,我们就可以直接通过匹配的情况来确定选中的路径。
小Ho:这个我懂了,但是如何保证这样就能得到最小的路径覆盖呢?
小Hi:你想想,每一条路径起点有什么特殊的地方?
小Ho:路径的起点入度为0...哦!我知道了。
如果一个点是路径起点的话,它在B部的节点一定是没有匹配上的。
经过最大匹配算法后,B部剩下没有被匹配的点一定是最少的,也就对应了最小需要的路径数。
所以最小路径覆盖的结果才是N-最大匹配数。
小Hi:正是这样,这样问题也就解决了。接下来第二个问题,怎么用网络流来解决二分匹配呢?
小Ho:上一次我们讲了二分多重匹配,二分匹配不就是它的简化版么。
只需要把源点s到A部的边和B部到汇点t的边容量限定为1就可以了!
小Hi:嗯,那么就只差最后一步了。
小Ho:这我也知道!实现嘛,交给我
代码:
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <stdlib.h>
#include <iomanip>
#include <fstream>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define maxn 1010
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define mem(a , b) memset(a , b , sizeof(a))
#define LL long long
#define ULL unsigned long long
#define FOR(i , n) for(int i = 1 ; i<= n ; i ++)
typedef pair<int , int> pii;
int n , m , ed;
vector<int>v[maxn];
int vis[maxn] , path[maxn] , a[maxn][maxn];
int flow[maxn] , ans;
bool BFS()
{
mem(vis , 0);
mem(path , -1);
mem(flow , 0);
queue<int>q;
while(!q.empty()) q.pop();
q.push(0);
vis[0] = 1;
flow[0] = INF;
while(!q.empty())
{
int cur = q.front();
q.pop();
if(cur == ed) return 1;
for(int i = 0 ; i < v[cur].size() ; i ++)
{
if(!vis[v[cur][i]] && a[cur][v[cur][i]] > 0)
{
vis[v[cur][i]] = 1;
flow[v[cur][i]] = min(flow[cur] , a[cur][v[cur][i]]);
path[v[cur][i]] = cur;
q.push(v[cur][i]);
}
}
}
return 0;
}
int main()
{
while(scanf("%d %d" , &n , &m) != EOF)
{
int s , to;
mem(a , 0);
ed = n + n + 1;
for(int i = 0 ; i < m ; i ++)
{
scanf("%d %d" , &s , &to);
v[s].push_back(to + n);
v[to+n].push_back(s);
a[s][to+n] = 1;
}
for(int i = 1 ; i <= n ; i ++)
{
v[0].push_back(i);
v[i].push_back(0);
a[0][i] = 1;
v[i+n].push_back(ed);
v[ed].push_back(i+n);
a[i+n][ed] = 1;
}
ans = 0;
while(BFS())
{
ans += flow[ed];
int fir = ed , sec = path[fir];
while(sec != -1)
{
a[fir][sec] += flow[ed];
a[sec][fir] -= flow[ed];
fir = sec;
sec = path[fir];
}
}
printf("%d\n" , n - ans);
}
return 0;
}
相关文章推荐
- hihoCoder 1394 : 网络流四·最小路径覆盖 (网络流学习#4 记录)
- [HihoCoder1394]网络流四·最小路径覆盖
- hihocoder 118周 网络流四·最小路径覆盖(二分匹配,好题)
- 网络流四·最小路径覆盖 HihoCoder - 13 4000 94
- hiho #1394 : 网络流四·最小路径覆盖
- #1394 : 网络流四·最小路径覆盖
- hiho一下 第118周 #1394 : 网络流四·最小路径覆盖 【网络流------ 最小路径覆盖 + 最大匹配 = n 】
- 【loj】#6002. 「网络流 24 题」最小路径覆盖
- 网络流二十四题之三 —— 最小路径覆盖问题(PATH)
- [网络流专练3][最小路径覆盖问题]
- 网络流24题之T3 最小路径覆盖问题
- 线性规划与网络流24——最小路径覆盖问题
- COGS728. [网络流24题] 最小路径覆盖问题
- 线性规划与网络流24题——03最小路径覆盖问题
- COGS 728. [网络流24题] 最小路径覆盖问题
- [HIHO1394]最小路径覆盖(二分匹配,最小路径覆盖)
- 网络流24题3 最小路径覆盖问题
- 网络流四·最小路径覆盖
- 最小路径覆盖问题 (网络流解法)
- 线性规划与网络流24题——03最小路径覆盖问题
