数值方法：多项式插值

数值方法：多项式插值

概述–插值方法

一维的数值插值方法，包括但不仅包括：

线性插值

Lagrange插值

Newton插值

Hermite插值

三次样条插值

sinc插值

小波插值

多项式插值

首先，多项式插值是基本的方法，除了上面的Lagrange方法与Newton方法，还有Aitken方法与Neville方法，由于多项式插值定理：

定理1 给定n+1个相异节点 x0,x1,⋯,xn∈[a,b]，以及n+1个函数值f(x0),f(x1),⋯,f(xn)，那么存在唯一的n次多项式p∈Pn满足插值条件

p(xi)=f(xi),i=0,1,⋯,n

由此可见，不同的多项式插值方法对于同样的插值问题的插值结果是一致的。

Hermite插值

多项式插值仅要求在插值节点x0,x1,...,xn∈[a,b]处的插值多项式与被插值函数相等。Hermite插值也是多项式插值，不过对于每个节点，不仅要求函数值相等，还要求节点处的一阶导数，甚至高阶导数相等。

定理2 设f∈C1[a,b]给定n+1个相异节点 x0,x1,⋯,xn∈[a,b]，那么存在唯一的多项式H2n+1∈P2n+1满足插值条件

{H2n+1(xj)=f(xj),H′2n+1(xj)=f′(xj),j=0,1,⋯,n

三次样条插值

高次多项式插值时由于出现的Runge现象不一定能达到高精度，因此分段低次的多项式插值是一个有效解决方法。

定义 对于区间[a,b]的一个剖分Δ:a=x0,x1,⋯,xn=b， 如果S为满足以下条件的函数： (1)S∈C2[a,b]，(2)在每个子区间[xj,xj+1]上是三次多项式，则称S是关于剖分Δ的一个三次样条函数。

sinc插值

多项式插值是时域的插值方法，sinc函数对应的频域函数是理想矩形窗，是一种频域的插值方法，相关应用设计的信号处理、傅里叶变换方面的知识。理论上，经过周期采样的信号在恢复时使用sinc函数时效果更好。

小波插值

据说是比较前沿的领域，目前信号处理技术多是以三角函数为基函数对目标函数进行分析，相关的变换是傅里叶变化，分析方法是频域分析方法。小波理论使用的是一组小波正交基，以此对目标函数进行分析。

（目前对小波理论并不了解，有待进一步研究。）

多项式插值方法

Lagrange方法

function [f]=interpolationLangrange(xx,ff,x)

f=0;
nx=length(xx)-1;

for i=0:nx
li=1;
for j=0:nx
if(j~=i)
li = li*(x-xx(j+1))/(xx(i+1)-xx(j+1));
end
end
f= f+ ff(i+1)*li;
end

end

Newton方法

function [f,nn]=interpolationNewton(xx,ff,x)

nx=length(xx)-1;
fnew=ff;
for j=1:nx
for i=j:nx
fnew(i+1)=(ff(i+1)-ff(i))/(xx(i+1)-xx(i+1-j));
end
ff(j+1:nx+1)=fnew(j+1:nx+1);
end
f=ff(1);
for j=1:nx
xt=1;
for i=1:j
xt=xt*(x-xx(i));
end
f=f + ff(j+1)*xt;
end
nn=ff;

end

算例

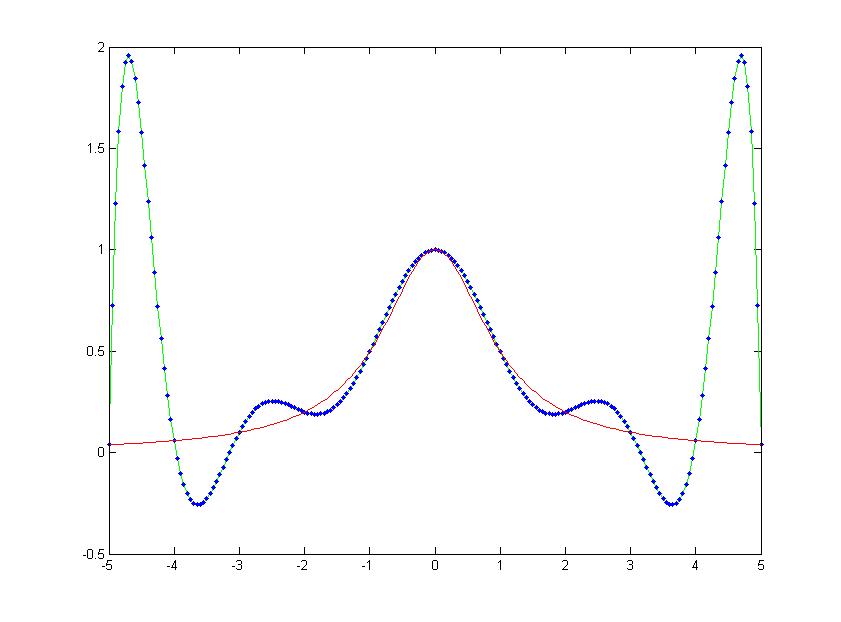
使用上述Lagrange与Newton方法对函数11+x2在区间[−5,5]上进行10阶插值。

红线为函数值，绿线为Lagrange方法插值结果，蓝点为Newton方法插值结果。