平面的投影变换(4)——利用虚圆点进行相似性校正
2016-09-20 11:11
1571 查看
1. 虚圆点和对偶二次曲线
定义(虚圆点, circular point):无穷线 l∞ 上有一对共轭复数的理想点在相似性变换下是固定不动的,这两个点的归一化坐标是
I = (1,i, 0)T,
J =(1, -i, 0)T.
这两个点是一个圆与无穷线 l∞ 的两个交点,叫虚圆点,或绝对点。
定理(虚圆点的相似性变换):虚圆点 I,J
在投影变换 H 下固定不动,当且仅当 H 是相似性变换。
找到虚圆点,就可以恢复相似性属性(角度,长度比例)。
定义(虚圆点的对偶二次曲线, dual conic):C*∞ = IJT
+ JIT
它的归一化坐标是:
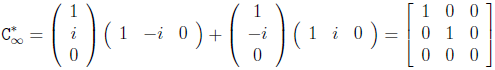
和虚圆点一样,C*∞ 在相似性变换下也是固定不动的,
定理(C*∞的相似性变换):对偶二次曲线C*∞在投影变换H
下固定不动,当且仅当 H 是相似性变换。
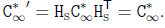
定理:无穷线 l∞ 是 C*∞
的零空间。
证明:虚圆点位于无穷线上,因此有 IT l∞ = JT l∞ =
0,从而
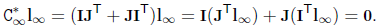
2. 投影变换中的夹角和距离比例
在欧式几何中,设两条直线
l = (l1, l2, l3)T和m =(m1, m2, m3)T,其法线分别为 (l1, l2)T和 (m1, m2)T,则它们的夹角等于法线的内积
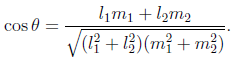
在投影变换中,夹角定义为
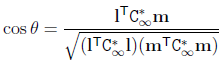
其中C*∞是循环点的对偶二次曲线。这个定义具有对投影变换的不变性,说明在投影平面中,只要确定了C*∞的投影,则可直接求出夹角。
定理:如果 lTC*∞m
= 0,则 l 和 m 正交。
三角形的边长比例为d(b,c):d(a,c) = sin α:
sin β,因此,既然夹角可求,那么只要确定了C*∞的投影,距离比例也可直接从投影平面中求出。

3. 相似性校正
与仿射校正需要求得无穷线 l∞ 的投影一样,相似性校正需要求得虚圆点 I, J 的投影。假设在投影平面中虚圆点已经被找到,则通过投影变换
H 将它变换到无穷线 l∞ 上的归一化位置,即(1, ±i,
0)T,则变换得到的平面是世界平面的相似性变换。
同样,如果在投影平面中找到C*∞的投影 C*'∞ =
H C*∞ HT,则也可以用来进行相似性校正。方法是:对 C*'∞ 进行奇异值分解,得到
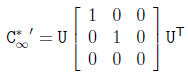
则用于相似性校正的投影变换 H = U。
4. 利用正交线对求C*'∞
利用投影变换的级联形式:

从而dual conic投影C*'∞ 具有如下形式:
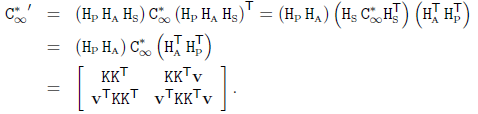
可见投影分量 v 和仿射分量 K 可以从投影C*'∞中求出,而相似性变换的信息在投影C*'∞中丢失了。可见C*'∞是个对称阵,可以写成如下形式:

下面讲述在投影变换平面上,如何利用直角的投影来求C*'∞:
(1)
在世界坐标系下,两条正交直线l 和m 的夹角为lT C*∞ m =
0。
(2)在投影平面中,这两条直线的投影 l' 和m'
的夹角仍然为0,即 l'T C*'∞ m'
= 0,可以写成如下形式
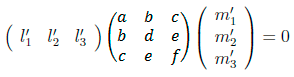
(3) 令向量 c = (a,b,c,d,
e, f)T,则上式可以写成如下形式,构成一个约束条件
(l'1m'1,
l'1m'2 + l'2m'1, l'1m'3 + l'3m'1, l'2m'2, l'2m'3 + l'3m'2, l'3m'3)c
= 0
(4) 在投影平面中找到5个正交对,则形成5个约束条件,构成1个5x6系数矩阵,而向量c 是这个矩阵的零空间,从而向量c 可依比例因子求出,进而得到C*'∞。
上述过程也可以先对投影图像进行仿射校正,在C*'∞中去除投影分量v
,然后在校正后的仿射变换平面中求出C*'∞,从而简化计算。这是一种分层(stratification)的方法。
定义(虚圆点, circular point):无穷线 l∞ 上有一对共轭复数的理想点在相似性变换下是固定不动的,这两个点的归一化坐标是
I = (1,i, 0)T,
J =(1, -i, 0)T.
这两个点是一个圆与无穷线 l∞ 的两个交点,叫虚圆点,或绝对点。
定理(虚圆点的相似性变换):虚圆点 I,J
在投影变换 H 下固定不动,当且仅当 H 是相似性变换。
找到虚圆点,就可以恢复相似性属性(角度,长度比例)。
定义(虚圆点的对偶二次曲线, dual conic):C*∞ = IJT
+ JIT
它的归一化坐标是:
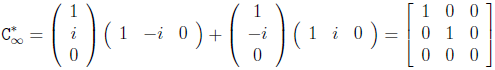
和虚圆点一样,C*∞ 在相似性变换下也是固定不动的,
定理(C*∞的相似性变换):对偶二次曲线C*∞在投影变换H
下固定不动,当且仅当 H 是相似性变换。
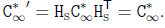
定理:无穷线 l∞ 是 C*∞
的零空间。
证明:虚圆点位于无穷线上,因此有 IT l∞ = JT l∞ =
0,从而
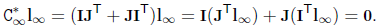
2. 投影变换中的夹角和距离比例
在欧式几何中,设两条直线
l = (l1, l2, l3)T和m =(m1, m2, m3)T,其法线分别为 (l1, l2)T和 (m1, m2)T,则它们的夹角等于法线的内积
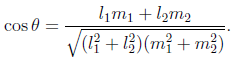
在投影变换中,夹角定义为
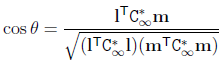
其中C*∞是循环点的对偶二次曲线。这个定义具有对投影变换的不变性,说明在投影平面中,只要确定了C*∞的投影,则可直接求出夹角。
定理:如果 lTC*∞m
= 0,则 l 和 m 正交。
三角形的边长比例为d(b,c):d(a,c) = sin α:
sin β,因此,既然夹角可求,那么只要确定了C*∞的投影,距离比例也可直接从投影平面中求出。

3. 相似性校正
与仿射校正需要求得无穷线 l∞ 的投影一样,相似性校正需要求得虚圆点 I, J 的投影。假设在投影平面中虚圆点已经被找到,则通过投影变换
H 将它变换到无穷线 l∞ 上的归一化位置,即(1, ±i,
0)T,则变换得到的平面是世界平面的相似性变换。
同样,如果在投影平面中找到C*∞的投影 C*'∞ =
H C*∞ HT,则也可以用来进行相似性校正。方法是:对 C*'∞ 进行奇异值分解,得到
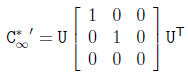
则用于相似性校正的投影变换 H = U。
4. 利用正交线对求C*'∞
利用投影变换的级联形式:

从而dual conic投影C*'∞ 具有如下形式:
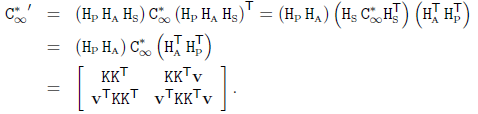
可见投影分量 v 和仿射分量 K 可以从投影C*'∞中求出,而相似性变换的信息在投影C*'∞中丢失了。可见C*'∞是个对称阵,可以写成如下形式:

下面讲述在投影变换平面上,如何利用直角的投影来求C*'∞:
(1)
在世界坐标系下,两条正交直线l 和m 的夹角为lT C*∞ m =
0。
(2)在投影平面中,这两条直线的投影 l' 和m'
的夹角仍然为0,即 l'T C*'∞ m'
= 0,可以写成如下形式
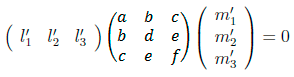
(3) 令向量 c = (a,b,c,d,
e, f)T,则上式可以写成如下形式,构成一个约束条件
(l'1m'1,
l'1m'2 + l'2m'1, l'1m'3 + l'3m'1, l'2m'2, l'2m'3 + l'3m'2, l'3m'3)c
= 0
(4) 在投影平面中找到5个正交对,则形成5个约束条件,构成1个5x6系数矩阵,而向量c 是这个矩阵的零空间,从而向量c 可依比例因子求出,进而得到C*'∞。
上述过程也可以先对投影图像进行仿射校正,在C*'∞中去除投影分量v
,然后在校正后的仿射变换平面中求出C*'∞,从而简化计算。这是一种分层(stratification)的方法。
相关文章推荐
- 平面的投影变换(3)——利用无穷线进行仿射校正
- 利用multiprocessing多进程模块进行影像校正
- 遥感影像几何纠正-正射校正-利用在线谷歌地图直接对影像进行几何校正
- 利用Turbo C进行平面二维图形的平移,旋转,缩放,对称
- 利用matlab和opencv进行摄像头校正
- 利用GDAL进行多项式几何校正校正新思路
- 利用OpenCV进行图像伽马校正
- 利用 Calibration Toolbox for Matlab 工具箱进行双目立体校正
- 利用kd树进行平面内最近点搜索
- (贪心5.2.3)POJ 1065 Wooden Sticks(利用数据有序化来进行贪心选择)
- 利用ffmpeg进行摄像头提取视频编码为h264通过RTP发送数据到指定的rtp地址
- 利用NUnit对类、方法进行原子级测试
- 读书笔记2:利用Python进行数据分…
- 利用MemoryAnalyzer进行OutOfMemoryError的诊断分析 .
- 利用js将图片地址进行转义
- 利用python进行数据分析笔记
- 利用Project Tango进行室内三维建模 精度评定
- 利用封装、继承对Java代码进行优化
- ms js利用ado.stream+msxml进行二进制读文件转base64字符输出与反转(提供工具)
- 利用BeanMap进行对象与Map的相互转换
