树状数组和线段树

树状数组

树状数组的概念

树状数组(binary indexed tree)是一种设计新颖的数组结构，它能够高效地获取数组中连续n个数的和。

树状数组通常用于解决以下问题：数组{a}中的元素可能不断地被修改，怎样才能快速地获取连续几个数的和？

树状数组的基本操作

传统数组(共n个元素)的元素修改和连续元素求和的复杂度分别为O(1)和O(n)。树状数组通过将线性结构转换成伪树状结构（线性结构只能逐个扫描元素，而树状结构可以实现跳跃式扫描），使得修改和求和的复杂度均为O(lgn)，大大提高了整体效率。

观察下面这张图，数组下标从1开始。



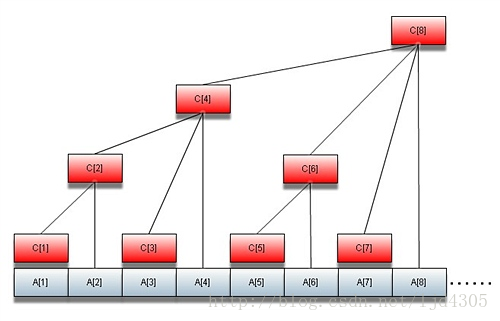
令这棵树的结点编号为C1，C2…Cn。令每个结点的值为这棵树的值的总和，那么容易发现：

　　

C1 = A1
　　C2 = A1 + A2
　　C3 = A3
　　C4 = A1 + A2 + A3 + A4
　　C5 = A5
　　C6 = A5 + A6
　　C7 = A7
　　C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
　　C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16

这里有一个有趣的性质：

设节点编号为x，那么这个节点管辖的区间为2^k（其中k为x的二进制形式的末尾0的个数）个元素。因为这个区间最后一个元素必然为Ax。(管辖区间就是记录的区间个数，1,3,5,7,9为1；2,6为2；4为4；8为8)

所以很明显：

Cn = A[n – 2^k + 1] + ... + A

那么如何算这个2^k呢？其实它就等于

x^(x–1)

。可以定义一个方法：

int lowbit(int x)
{
return x^(x–1);
}

想要查询一个SUM(n)，可以依据如下算法即可(求a[0]~a
的和）：

令sum = 0，转第二步；

假如n <= 0，算法结束，返回sum值，否则sum = sum + Cn，转第三步；

令 n = n – lowbit(n)，转第二步。

可以看出，这个算法就是将这一个个区间的和全部加起来，具体实现如下：

int sum(int i)
{
int ans = 0;
while(i > 0)
{
ans += ar[i];
i -= lowbit(i);
}
return ans;
}

那么修改某元素呢，修改一个节点，必须修改其所有祖先，最坏情况下为修改第一个元素，最多有log(n)的祖先。所以修改算法如下（给某个结点i加上x）：

当i > n时，算法结束，否则转第二步；

Ci = Ci + x， i = i + lowbit(i)转第一步；

i = i +lowbit(i)

这个过程实际上也只是一个把末尾1补为0的过程。完整的修改（这里是加某个数w）的实现如下：

void update(int i, int w)
{
while(i <= n)
{
ar[i] += w;
i += lowbit(i);
}
}

树状数组的完整C语言实现：

下面给出树状数组完整的C语言实现：

//求2^k
int lowbit(int x)
{
return x^(x–1);
}

//求前n项和
int sum(int i)
{
int ans = 0;
while(i > 0)
{
ans += ar[i];
i -= lowbit(i);
}
return ans;
}

//修改某个元素的大小
void update(int i, int w)
{
while(i <= n)
{
ar[i] += w;
i += lowbit(i);
}
}

线段树

线段树支持对一个数列的求和、单点修改、求最值（最大、最小）、区间修改（需要lazy标记，暂不讲解）。这几种操作，时间复杂度是（logn）级别的，是一种十分优秀的数据结构。因此其获得了广泛的应用。

线段树基本性质

定义：顾名思义，它是一种树形结构，但每个节点不是通常意义上的单点，而是一条线段，每条线段包含着一些值，其中最主要的是起始端点和结束端点，记作 left，right 。

那么该如何划分线段树呢？我们采用二分的思想，即每次将一段取半，再进行接下来的操作，这样综合了操作的方便程度和时间复杂度。因为线段树通过二分得来，所以线段树是一颗二叉树。这也方便了对儿子的查找。

记某节点为T(a, b)，参数a,b表示区间

[a,b]

，其中b-a称为区间的长度，记为L。若L>1，则有当前节点的左儿子节点

[a, (a+b) / 2]

，右儿子节点

[(a+b) / 2,b]

；若L=1 ，则当前节点为叶节点。

线段树的建立

仅仅知道模型还是不够的，建树的过程是线段树的关键。从1号开始，左端是1，右端是n。下面的代码中，

i<<1即是i*2

，

i<<1 | 1即是i*2+1

。

//更新i节点维护的值（求和，最大值等）
void update(int i) {
node[i].sum=node[i*2].sum+node[i*2 + 1].sum;
node[i].maxx=max(node[i*2].maxx,node[i*2 + 1].maxx);
}

void build(int i,int l,int r) {
node[i].left=l;node[i].right=r;
//若l==r,则当前的树节点是真正意义上的点
if(l==r){
node[i].maxx=a[l];//最大值就是本身的值
node[i].sum=a[l];//区间的和就是本身的值
return;
}
int mid=(l+r)/2;
//根据完全二叉树的知识，左儿子是i*2,右儿子是i*2+1
build(i*2,l,mid);
build((i*2+1,mid+1,r);
update(i);
}

应用：区间求和

这是线段树的一个典型算法，其他的很多应用都是从中转化的。

为了求和我们定义一个函数

sum(int i,int l,int r)

， i 是开始的树节点，我们默认为1。l 是区间的开始点，它的标号是在数列中的标号，r 是结束点。

int sum(int i,int l,int r) {
//若树节点的左右区间与查找区间相同，直接返回其维护的sum
if(node[i].l==l && node[i].r==r) return node[i].sum;
//确定该树节点的中点以确定继续查找左儿子还是右儿子
int mid=(node[i].l+node[i].r)/2;
//若查找区间最右端小于中点，则该区间完全包含于左儿子中
if(r<=mid) return sum(i*2,l,r);
//最左端大于中点，查找右儿子
else if(l>mid) return sum((i<<1)|1,l,r);
//若跨越中点，查找左儿子 l 到 mid ,和右儿子的 mid+1 到 r 并返回值
else return sum(i<<1,l,mid)+sum((i<<1)|1,mid+1,r);
}

应用：区间求最值

和区间求和类似，只是用到了不同的辅助变量maxx。

int Max(int i,int l,int r) {
if(node[i].l==l && node[i].r==r) return node[i].maxx;
int mid=(node[i].l+node[i].r)/2;
if(r<=mid) return Max(i<<1,l,r);
else if(l>mid) return Max((i<<1)|1,l,r);
else return max(Max(i<<1,l,mid),Max((i<<1)|1,mid+1,r));
}

单点更新

当前计算到的点为i，把数列中的第k个元素加v：

void add(int i,int k,int v) {
if(node[i].l==k && node[i].r==k){//因为更改的单点，所以左右端点均和k相等
node[i].sum+=v;
node[i].maxx+=v;
return;
}
int mid=(node[i].l+node[i].r)/2;
if(k<=mid) add(i*2,k,v);//若k小于mid则k在树节点i的左子树中
else add(i*2+1,k,v);//反之
update(i);//更新当前的点i
}

模板：完整的线段树实现

#include<iostream>
#include<cstdio>
using namespace std;
struct tree{
int l,r,sum,maxx;
};
tree node[100];
int n,m,a[100];
//更新节点i
void update(int i) {
node[i].sum=node[i<<1].sum+node[(i<<1)|1].sum;
node[i].maxx=max(node[i<<1].maxx,node[(i<<1)|1].maxx);
}

void build(int i,int l,int r) {
node[i].l=l;node[i].r=r;
if(l==r) {
node[i].maxx=a[l];
node[i].sum=a[l];
return;
}
int mid=(l+r)/2;
build(i*2,l,mid);
build(i*2,mid+1,r);
update(i);
}

void add(int i,int k,int v) {
if(node[i].l==k && node[i].r==k){//因为更改的是单点，所以左右端点均和k相等
node[i].sum+=v;
node[i].maxx+=v;
return;
}
int mid=(node[i].l+node[i].r)/2;
if(k<=mid) add(i*2,k,v);//若k小于mid则k在树节点i的左子树中
else add(i*2+1,k,v);//反之
update(i);//更新当前的点i
}

int sum(int i,int l,int r) {
//若树节点的左右区间与查找区间相同，直接返回其维护的sum
if(node[i].l==l && node[i].r==r) return node[i].sum;
//确定该树节点的中点以确定继续查找左儿子还是右儿子
int mid=(node[i].l+node[i].r)/2;
//若查找区间最右端小于中点，则该区间完全包含于左儿子中
if(r<=mid) return sum(i*2,l,r);
//最左端大于中点，查找右儿子
else if(l>mid) return sum((i<<1)|1,l,r);
//若跨越中点，查找左儿子 l 到 mid ,和右儿子的 mid+1 到 r 并返回值
else return sum(i<<1,l,mid)+sum((i<<1)|1,mid+1,r);
}

int Max(int i,int l,int r) {
if(node[i].l==l && node[i].r==r) return node[i].maxx;
int mid=(node[i].l+node[i].r)/2;
if(r<=mid) return Max(i<<1,l,r);
else if(l>mid) return Max((i<<1)|1,l,r);
else return max(Max(i<<1,l,mid),Max((i<<1)|1,mid+1,r));
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
build(1,1,n);
for(int i=1;i<=m;i++) {
int c,a,b;
scanf("%d%d%d",&c,&a,&b);
if(c==1) printf("%d\n",sum(1,a,b));
else if(c==2) add(1,a,b);
else if(c==3) printf("%d\n",Max(1,a,b));
}
}

PS：

线段树的高级用法包括延迟标记，它主要用于成段更新时加快速度。这里暂不作详述。

树状数组与线段树的简单比较

树状数组和线段树都是一种擅长处理区间的数据结构。它们最大的区别之一就是线段树是一颗完美二叉树，而树状数组（BIT）相当于是线段树中每个节点的右儿子去掉。

用树状数组能够解决的问题，用线段树肯定能够解决，反之则不一定。但是树状数组有一个明显的好处就是较为节省空间，实现要比线段树要容易得多，而且在处理某些问题的时候使用树状数组效率反而会高得多。