线性回归 linear regression 以及 lasso ridge 解析
2016-09-01 15:24
225 查看
在知乎问答中,看到一个很好的回答,记录到此篇博文中,以便于后期查找。
普通的线性回归的公式是这样的
<img src="https://pic1.zhimg.com/55348094cfdfad25e96219b20d310424_b.png" data-rawwidth="1468" data-rawheight="814" class="origin_image zh-lightbox-thumb" width="1468"
data-original="https://pic1.zhimg.com/55348094cfdfad25e96219b20d310424_r.png">y是
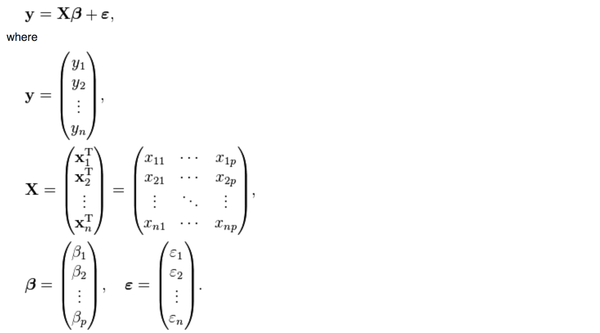
y是被解释变量,X是p个解释变量,我们手里有n组(y,
X)的样本,然后想要通过这些样本找到一个向量beta使得
<img src="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_b.png" data-rawwidth="1034" data-rawheight="86" class="origin_image zh-lightbox-thumb" width="1034" data-original="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_r.png">被最小化,满足这个最小化条件的beta就是线性回归要寻找的beta,数学上可以证明这个问题是有通解的:

被最小化,满足这个最小化条件的beta就是线性回归要寻找的beta,数学上可以证明这个问题是有通解的:
<img src="https://pic1.zhimg.com/4d97c44fe478275c625b41b895cdb874_b.png" data-rawwidth="1796" data-rawheight="84" class="origin_image zh-lightbox-thumb" width="1796" data-original="https://pic1.zhimg.com/4d97c44fe478275c625b41b895cdb874_r.png">也就是说,只有我们手里有X和Y这两个矩阵(向量),把它们带入上面的公式就能得到我们想要的beta,然后就能用beta和新的Xi来对未知的Yi进行预测了。

也就是说,只有我们手里有X和Y这两个矩阵(向量),把它们带入上面的公式就能得到我们想要的beta,然后就能用beta和新的Xi来对未知的Yi进行预测了。
然而,上面这个公式有一个问题,<img src="https://pic1.zhimg.com/e8f2088ae81f9b4feb806dbf398fb2fc_b.png" data-rawwidth="112" data-rawheight="60" class="content_image" width="112">这两个矩阵相乘的结果,一个p*p的矩阵(p是解释变量的个数),一定是可逆的吗?不可逆的话刚才算beta的公式不就没有意义了吗?
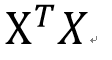
这两个矩阵相乘的结果,一个p*p的矩阵(p是解释变量的个数),一定是可逆的吗?不可逆的话刚才算beta的公式不就没有意义了吗?
幸运的是,在实际生活中,只要我们的数据真的是随机抽取的,这个矩阵一般都是可逆的。
不幸的是,有一种存在叫做almost singular。
一个方阵(行数=列数, 比如上面那个p*p矩阵)一定可以被归类到以下两种情况:
singular: 行列式|X|=0,特征根中至少有一个是0,不满秩,不可以求逆。
nonsingular: 行列式|X|不等于0,特征根都不等于0,满秩,可以求逆。
这个矩阵
<img src="https://pic1.zhimg.com/e8f2088ae81f9b4feb806dbf398fb2fc_b.png" data-rawwidth="112" data-rawheight="60" class="content_image" width="112">肯定是nonsingular的可以求逆,但是在一些情况下(比如multicollinearity),这个矩阵的行列式的值可能非常非常非常小(比如0.000000001),于是X只要有一个微小的变化,它的逆矩阵就会有一个很大很大的变化,导致你用不同的样本估计出来的beta的差别非常非常大,这样的矩阵就叫almost
singular。
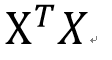
肯定是nonsingular的可以求逆,但是在一些情况下(比如multicollinearity),这个矩阵的行列式的值可能非常非常非常小(比如0.000000001),于是X只要有一个微小的变化,它的逆矩阵就会有一个很大很大的变化,导致你用不同的样本估计出来的beta的差别非常非常大,这样的矩阵就叫almost
singular。
almost singular: 行列式|X|几乎等于0,特征根有一个或多个接近于0,满秩,可以求逆,但是对X进行微小的改变会导致逆矩阵发生巨大的改变。
大家想一想,如果你用1点钟收集到的数据估出来的参数等于100,3点钟收集到的数据估出来的参数等于100000,那你到底要用哪一个?到底哪一个是对的?你并不知道。
这个问题就是楼上有人提出的“estimator 的数值解可能不存在/极不稳定”的情况。
那么如何解决呢?当然要对症下药啦。既然这个矩阵的行列式近似等于0,那我在它的对角线上全部加上一个常数不就行了嘛?
于是ridge regression就被发明出来了:
<img src="https://pic3.zhimg.com/0e9666dfb0438de6594c79a8a68bcf0e_b.png" data-rawwidth="2124" data-rawheight="418" class="origin_image zh-lightbox-thumb" width="2124" data-original="https://pic3.zhimg.com/0e9666dfb0438de6594c79a8a68bcf0e_r.png">其实就是在刚刚Beta的解的公式的基础上进行了微小的调整,I是单位矩阵,lamda是通过cross
validation来确定的,并不是需要估计的参数。这个调整就是楼上有人说的regularization。
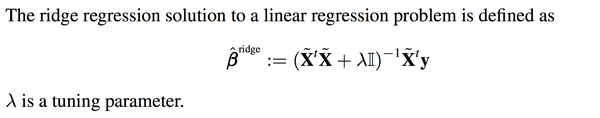
其实就是在刚刚Beta的解的公式的基础上进行了微小的调整,I是单位矩阵,lamda是通过cross
validation来确定的,并不是需要估计的参数。这个调整就是楼上有人说的regularization。
你可能会很疑惑,如果说线性回归是在最小化下面这个方程:
<img src="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_b.png" data-rawwidth="1034" data-rawheight="86" class="origin_image zh-lightbox-thumb" width="1034" data-original="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_r.png">那ridge
regression是在最小化什么东西呢?数学上也可以证明,上面新的beta的解,其实就是在最小化下面这个式子:

那ridge
regression是在最小化什么东西呢?数学上也可以证明,上面新的beta的解,其实就是在最小化下面这个式子:
<img src="https://pic2.zhimg.com/78c918400ad37476191bd918189c5f81_b.png" data-rawwidth="1868" data-rawheight="176" class="origin_image zh-lightbox-thumb" width="1868" data-original="https://pic2.zhimg.com/78c918400ad37476191bd918189c5f81_r.png">其实就是在上面的式子后面多加了一项而已。
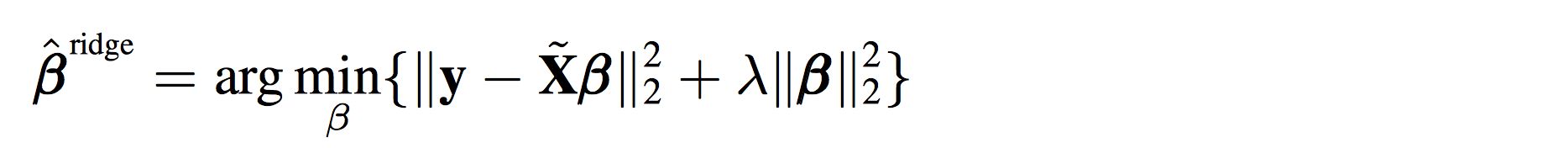
其实就是在上面的式子后面多加了一项而已。
你可能又要问了,多加的那一项凭什么是模长呢?不能把2-norm改成1-norm吗?
答案是可以的,这种情况就是lasso了:
<img src="https://pic4.zhimg.com/5db6de547bd3e8848c7905fedacf331b_b.png" data-rawwidth="2284" data-rawheight="472" class="origin_image zh-lightbox-thumb" width="2284" data-original="https://pic4.zhimg.com/5db6de547bd3e8848c7905fedacf331b_r.png">
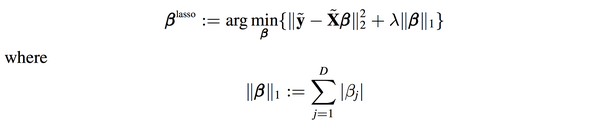
遗憾的是,lasso是不能像ridge regression和linear regression一样写出“显式解”的,必须用数值方法去近似上面的优化问题的解。
幸运的是,统计学家发现用lasso算出来的beta的很多项是0,也就是说你在估计参数的时候顺带着把model selection也一起做了,买一送一哦亲!
为什么会这样呢?上面有答主传了一副图:
<img src="https://pic2.zhimg.com/e67746f0be32a177681a85f44527a54d_b.png" data-rawwidth="500" data-rawheight="250" class="origin_image zh-lightbox-thumb" width="500" data-original="https://pic2.zhimg.com/e67746f0be32a177681a85f44527a54d_r.png">因为lasso选了1-norm,导致theta-lasso的范围“有棱有角”,在和normal
equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话,就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。
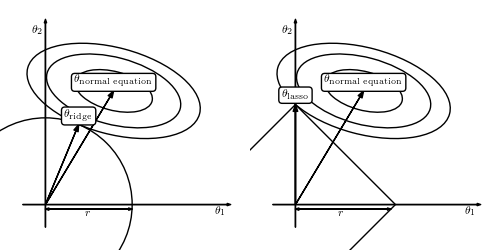
因为lasso选了1-norm,导致theta-lasso的范围“有棱有角”,在和normal
equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话,就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。
简而言之,
不想做数值优化,想要一个确定的解,选ridge regression吧!
不想做完参数估计还要做model selection挑选变量,选lasso吧!
可是新的问题又出现了,ridge regression选了2-norm,lasso选了1-norm,那我能不能把这个问题拓展到p-norm的情形呢?(这个p和刚才的解释变量的个数p是两个概念)
答案是可以的,只要p大于等于1就行了。
p为什么不能小于1?因为p小于1时刚才那幅图里的圆形和正方形会继续“往里陷”,变成下面的样子:
<img src="https://pic3.zhimg.com/906ec742ab56bae06650c4eadab43422_b.png" data-rawwidth="2568" data-rawheight="648" class="origin_image zh-lightbox-thumb" width="2568" data-original="https://pic3.zhimg.com/906ec742ab56bae06650c4eadab43422_r.png">这样这个集合就不是convex
set了,没有办法做最优化了,which is another long story。
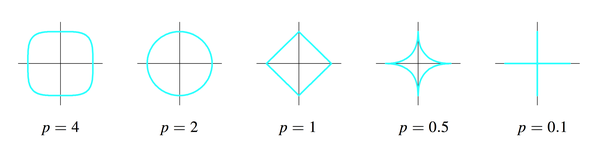
这样这个集合就不是convex
set了,没有办法做最优化了,which is another long story。
原文地址:https://www.zhihu.com/question/38121173
普通的线性回归的公式是这样的
<img src="https://pic1.zhimg.com/55348094cfdfad25e96219b20d310424_b.png" data-rawwidth="1468" data-rawheight="814" class="origin_image zh-lightbox-thumb" width="1468"
data-original="https://pic1.zhimg.com/55348094cfdfad25e96219b20d310424_r.png">y是

y是被解释变量,X是p个解释变量,我们手里有n组(y,
X)的样本,然后想要通过这些样本找到一个向量beta使得
<img src="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_b.png" data-rawwidth="1034" data-rawheight="86" class="origin_image zh-lightbox-thumb" width="1034" data-original="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_r.png">被最小化,满足这个最小化条件的beta就是线性回归要寻找的beta,数学上可以证明这个问题是有通解的:

被最小化,满足这个最小化条件的beta就是线性回归要寻找的beta,数学上可以证明这个问题是有通解的:
<img src="https://pic1.zhimg.com/4d97c44fe478275c625b41b895cdb874_b.png" data-rawwidth="1796" data-rawheight="84" class="origin_image zh-lightbox-thumb" width="1796" data-original="https://pic1.zhimg.com/4d97c44fe478275c625b41b895cdb874_r.png">也就是说,只有我们手里有X和Y这两个矩阵(向量),把它们带入上面的公式就能得到我们想要的beta,然后就能用beta和新的Xi来对未知的Yi进行预测了。

也就是说,只有我们手里有X和Y这两个矩阵(向量),把它们带入上面的公式就能得到我们想要的beta,然后就能用beta和新的Xi来对未知的Yi进行预测了。
然而,上面这个公式有一个问题,<img src="https://pic1.zhimg.com/e8f2088ae81f9b4feb806dbf398fb2fc_b.png" data-rawwidth="112" data-rawheight="60" class="content_image" width="112">这两个矩阵相乘的结果,一个p*p的矩阵(p是解释变量的个数),一定是可逆的吗?不可逆的话刚才算beta的公式不就没有意义了吗?
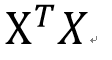
这两个矩阵相乘的结果,一个p*p的矩阵(p是解释变量的个数),一定是可逆的吗?不可逆的话刚才算beta的公式不就没有意义了吗?
幸运的是,在实际生活中,只要我们的数据真的是随机抽取的,这个矩阵一般都是可逆的。
不幸的是,有一种存在叫做almost singular。
一个方阵(行数=列数, 比如上面那个p*p矩阵)一定可以被归类到以下两种情况:
singular: 行列式|X|=0,特征根中至少有一个是0,不满秩,不可以求逆。
nonsingular: 行列式|X|不等于0,特征根都不等于0,满秩,可以求逆。
这个矩阵
<img src="https://pic1.zhimg.com/e8f2088ae81f9b4feb806dbf398fb2fc_b.png" data-rawwidth="112" data-rawheight="60" class="content_image" width="112">肯定是nonsingular的可以求逆,但是在一些情况下(比如multicollinearity),这个矩阵的行列式的值可能非常非常非常小(比如0.000000001),于是X只要有一个微小的变化,它的逆矩阵就会有一个很大很大的变化,导致你用不同的样本估计出来的beta的差别非常非常大,这样的矩阵就叫almost
singular。
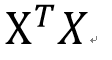
肯定是nonsingular的可以求逆,但是在一些情况下(比如multicollinearity),这个矩阵的行列式的值可能非常非常非常小(比如0.000000001),于是X只要有一个微小的变化,它的逆矩阵就会有一个很大很大的变化,导致你用不同的样本估计出来的beta的差别非常非常大,这样的矩阵就叫almost
singular。
almost singular: 行列式|X|几乎等于0,特征根有一个或多个接近于0,满秩,可以求逆,但是对X进行微小的改变会导致逆矩阵发生巨大的改变。
大家想一想,如果你用1点钟收集到的数据估出来的参数等于100,3点钟收集到的数据估出来的参数等于100000,那你到底要用哪一个?到底哪一个是对的?你并不知道。
这个问题就是楼上有人提出的“estimator 的数值解可能不存在/极不稳定”的情况。
那么如何解决呢?当然要对症下药啦。既然这个矩阵的行列式近似等于0,那我在它的对角线上全部加上一个常数不就行了嘛?
于是ridge regression就被发明出来了:
<img src="https://pic3.zhimg.com/0e9666dfb0438de6594c79a8a68bcf0e_b.png" data-rawwidth="2124" data-rawheight="418" class="origin_image zh-lightbox-thumb" width="2124" data-original="https://pic3.zhimg.com/0e9666dfb0438de6594c79a8a68bcf0e_r.png">其实就是在刚刚Beta的解的公式的基础上进行了微小的调整,I是单位矩阵,lamda是通过cross
validation来确定的,并不是需要估计的参数。这个调整就是楼上有人说的regularization。
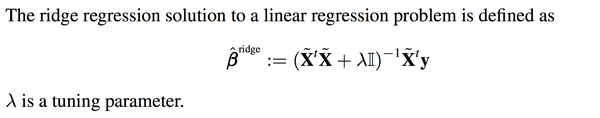
其实就是在刚刚Beta的解的公式的基础上进行了微小的调整,I是单位矩阵,lamda是通过cross
validation来确定的,并不是需要估计的参数。这个调整就是楼上有人说的regularization。
你可能会很疑惑,如果说线性回归是在最小化下面这个方程:
<img src="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_b.png" data-rawwidth="1034" data-rawheight="86" class="origin_image zh-lightbox-thumb" width="1034" data-original="https://pic1.zhimg.com/62848370d010e67d87d4bb80e1289688_r.png">那ridge
regression是在最小化什么东西呢?数学上也可以证明,上面新的beta的解,其实就是在最小化下面这个式子:

那ridge
regression是在最小化什么东西呢?数学上也可以证明,上面新的beta的解,其实就是在最小化下面这个式子:
<img src="https://pic2.zhimg.com/78c918400ad37476191bd918189c5f81_b.png" data-rawwidth="1868" data-rawheight="176" class="origin_image zh-lightbox-thumb" width="1868" data-original="https://pic2.zhimg.com/78c918400ad37476191bd918189c5f81_r.png">其实就是在上面的式子后面多加了一项而已。
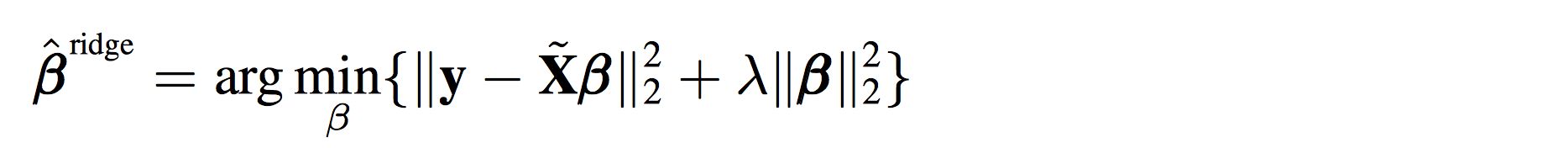
其实就是在上面的式子后面多加了一项而已。
你可能又要问了,多加的那一项凭什么是模长呢?不能把2-norm改成1-norm吗?
答案是可以的,这种情况就是lasso了:
<img src="https://pic4.zhimg.com/5db6de547bd3e8848c7905fedacf331b_b.png" data-rawwidth="2284" data-rawheight="472" class="origin_image zh-lightbox-thumb" width="2284" data-original="https://pic4.zhimg.com/5db6de547bd3e8848c7905fedacf331b_r.png">
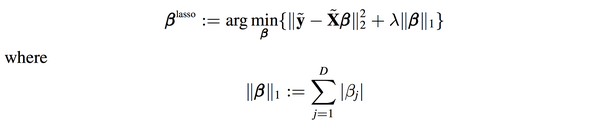
遗憾的是,lasso是不能像ridge regression和linear regression一样写出“显式解”的,必须用数值方法去近似上面的优化问题的解。
幸运的是,统计学家发现用lasso算出来的beta的很多项是0,也就是说你在估计参数的时候顺带着把model selection也一起做了,买一送一哦亲!
为什么会这样呢?上面有答主传了一副图:
<img src="https://pic2.zhimg.com/e67746f0be32a177681a85f44527a54d_b.png" data-rawwidth="500" data-rawheight="250" class="origin_image zh-lightbox-thumb" width="500" data-original="https://pic2.zhimg.com/e67746f0be32a177681a85f44527a54d_r.png">因为lasso选了1-norm,导致theta-lasso的范围“有棱有角”,在和normal
equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话,就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。

因为lasso选了1-norm,导致theta-lasso的范围“有棱有角”,在和normal
equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话,就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。
简而言之,
不想做数值优化,想要一个确定的解,选ridge regression吧!
不想做完参数估计还要做model selection挑选变量,选lasso吧!
可是新的问题又出现了,ridge regression选了2-norm,lasso选了1-norm,那我能不能把这个问题拓展到p-norm的情形呢?(这个p和刚才的解释变量的个数p是两个概念)
答案是可以的,只要p大于等于1就行了。
p为什么不能小于1?因为p小于1时刚才那幅图里的圆形和正方形会继续“往里陷”,变成下面的样子:
<img src="https://pic3.zhimg.com/906ec742ab56bae06650c4eadab43422_b.png" data-rawwidth="2568" data-rawheight="648" class="origin_image zh-lightbox-thumb" width="2568" data-original="https://pic3.zhimg.com/906ec742ab56bae06650c4eadab43422_r.png">这样这个集合就不是convex
set了,没有办法做最优化了,which is another long story。
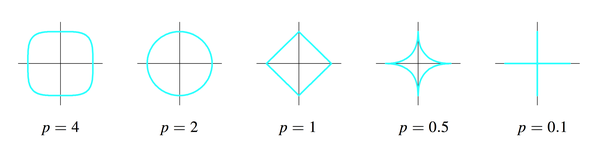
这样这个集合就不是convex
set了,没有办法做最优化了,which is another long story。
原文地址:https://www.zhihu.com/question/38121173
相关文章推荐
- 决策树、逻辑回归、线性回归使用时注意事项以及模型过拟合策略
- sklearn 源码解析 基本线性模型 岭回归 ridge.py(2)
- 线性回归之最小二乘法简要解析
- 线性回归以及局部加权回归
- sklearn 源码解析 基本线性模型 岭回归 ridge.py(1)
- 斯坦福大学(吴恩达) 机器学习课后习题详解 第六周 编程题 正则化线性回归以及方差与偏差
- 斯坦福大学机器学习课程笔记:线性回归以及梯度下降
- 线性回归的数学原理以及代码实现
- 稀疏矩阵线性解析库SPOOLES的简单应用
- SharpDevelop解析与学习心得之一------概况以及物理结构
- jQuery工作原理解析以及源代码示例
- Linux内存线性地址空间布局解析
- C++多彩的运算符语义以及对引用的语义解析
- 八种系统安全模式解析以及应用
- 命令行解析的规则以及Command Line Parser Library
- jQuery工作原理解析以及源代码示例
- 8种Windows安全模式解析以及应用
- [InnoDB系列] - 实例解析Innodb的隔离级别以及锁模式
- 资料:8种Windows安全模式解析以及应用
- java对xml全面解析,增,删,改,以及将java对象重新编组为xml文件
