透视变换的推导
2016-08-01 11:35
127 查看
参考网址:
http://www.codeguru.com/cpp/misc/misc/graphics/article.php/c10123/Deriving-Projection-Matrices.htm#page-3
http://blog.csdn.net/zhanghua1816/article/details/23121735
在3D图形学中所有的变换,其中透视变换是稍微复杂一点的。平移变换和缩放变换很容易明白。而旋转变换只要你能够明白基本的三角学也是可以很容易的推导出来的。如果你之前看过这个矩阵,你也许不是很直观地看出他是怎么来的。下面就是作者自己的推导过程喽!!!
对于刚接触图形学的新手来说,图形学是不是需要有很深厚的数学知识呢?其实也不必要有如此的畏惧。本文尽量从理解的角度来写,都是很简单易懂的推导。
1、什么是透视
计算机的显示器是二维的,而你想要将3D的东西展示成一张图片,就需要将3D几何物体通过一种方式转换为2D图片。这就是透视矩阵要做的事情。其中一种简单的透视方法就是忽略z轴,只用x和y坐标。
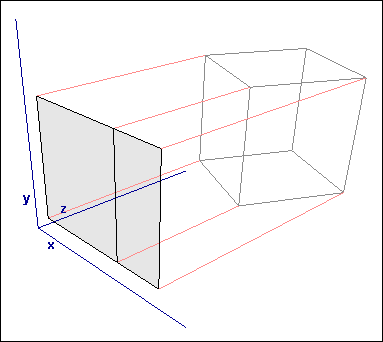
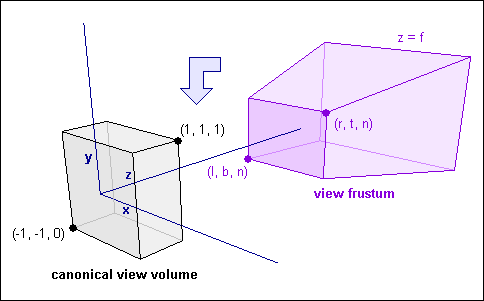
当然,这个方法简单,但是却不常用。对于初学者来说,不会将透视投到一个平面上。而将你的几何体投射到一个新的体内。这个体称为规范化视域体。对于不同的api来说,对于规范化视域体内的坐标是不同的。在D3D中,我们将这个规范化视域体扩展为(-1,-1,0)to(1,1,1)。当你的顶点被映射到规范化视域体内之后,只用到了点的x和y坐标,它被映射到屏幕上去。z坐标没有用处,但是z坐标在深度检测中会被用到。
上图中,使用的是左手坐标系,这也是D3D中使用的坐标系。这篇文章呢,也是用的是左手坐标系。
2、正交投影
正交投影有一个特点,就是所有的透视线和投影平面是垂直的。下图中会看到规范化视域体。

如上图,左下角是(-1,-1,0)而右上角是(1,1,1)。
如上图,你可以看到视锥体是通过6个平面限定的。
left:x = l
right:x = r
bottom:y = b
top:y = t
near:z = n
far:z = f
正交变换的特点是3D物体在空间中经过投影到平面上之后,保持大小相同。
三个坐标轴分别考虑怎么映射。这个涉及到从原始的视域体映射到规范化的视域体呢。下面我们已x轴为例子,看看如何从[l,r]映射到[-1,1]的范围内。
原始视域体内x的范围是:
l<=x<=r
将其两边同时减去l得到:
0<=x-l<=r-l
然后,不等式两边再同时除以r-l,这个值是你的视域体的宽度。
0<=(x-l)/(r-l)<=1
然后再乘以2,得到:
0<=2(x-l)/(r-l)<=2
然后再减去1
-1<=2(x-l)/(r-l) - 1<=1
然后得到:
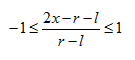
然后我们改写中间的项,写成px+q形式:
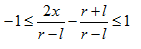
中间的就是用来将原始视域体内的点映射成规范化视域体内的点。

同样的对于y也是类似的映射方式,其结果为:

最后你需要把z轴也做映射。映射的范围是[0,1],而不是[-1,1]。
n<=z<=f
两边同时减去n得到:
0<=z-n<=f-n
然后两边再同时除以f-n,得到:
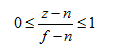
然后也写成pz+q的形式:
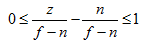
然后z即为:

这样我们就得到了,如下的等式:

写成矩阵的形式为:
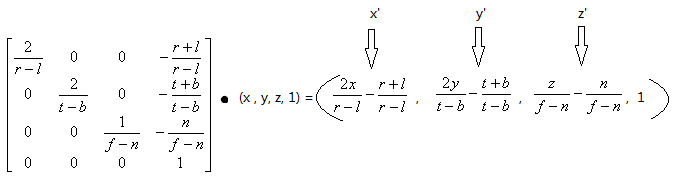
然后我们可以简化上面的矩阵,仅仅使用视域体的宽度和高度来改写,并且让r=-l,t=-b,那么
矩阵可以简化为:

然后我们再将这个矩阵,改写成一个缩放矩阵和一个平移矩阵的乘积:
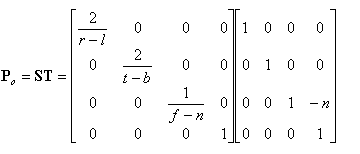
首先,将原始视锥体的近平面作为原点,即作为一个z轴的平移,所以使用平移矩阵。然后再将点映射到规范视锥体内,所以使用了一个缩放矩阵。
这个就得到正交投影矩阵了。
3、透视投影
透视投影与正交投影的不同点在于,透视投影的视锥体是一个削去尖的椎体,如下图所示:
利用相似三角形来推导透视之后的点:
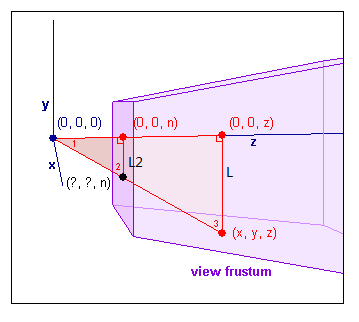
上图中L的距离等于:

然后我们因为L2这个线段与z轴的交点是在近平面上的,所以其z坐标为n;另外因为L的与z轴的交点的z坐标为就为z,那么根据相似三角形的知识可以知道L2的长度:

进一步的改写:
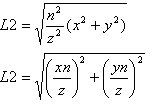
可以知道(x,y,z)经过透视之后得到的坐标为:
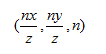
此时,回想上面的正交投影透视点(x,y,z)被映射到规范化视域体内的公式:

这里看到x和y的公式,那么此时我们把这里的x和y更换成nx/z,以及ny/z即可得到:
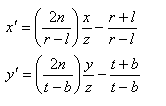
接着,对于上面的式子,两边同时乘以z之后得到:
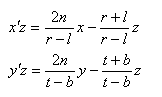
此时有了两个等式,我们还得往矩阵的上靠靠。如何将等式写成如下的形式:

这有写成这样的形式,才能方便改写为矩阵的形式。
注意此时我们得到了两个如下的等式:

如果再有一个z’z的等式,那么我们就得到了如下的:

这里构建如下的等式:
z’z = pz + q
其中,p和q是常量。
我们知道当z’=0时,z=n。当z’=1,z=f。代入上面的式子,可以求出p和q的值:

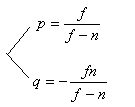
于是我们有了如下的式子:

此时我们有了3个式子:
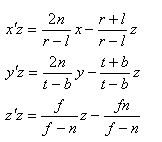
之前我们的4维矩阵最后一行永远是(0,0,0,1)所以w’=1,那么两边同时乘以z,得到:
w’z = z.
此时我们有了如下的四个式子:
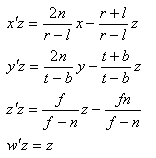
然后我们改写成矩阵的形式:
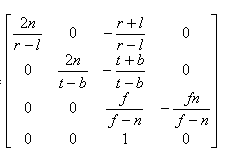
此时简化矩阵,令r=-l,t=-b,然后w表示r-l;h=t-b,得到简化的矩阵为:
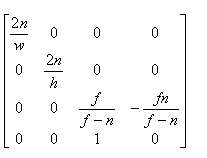
问题到这里已经基本解决了,最后我们的简化是与视域体的张角有关系,也很简单,如下图所示:
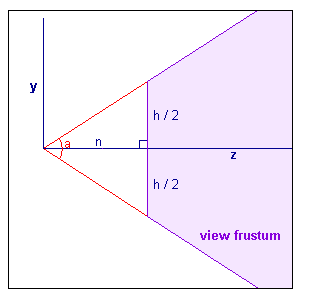
其中:

我们再次设定w/h,即视域体的宽高比为r。w为视域提的宽度,即r-l。h为视域体的高度,即t-b。
那么矩阵中的2n/w=2n/rh。
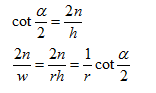
于是我们的矩阵简化为:

到这里我们的透视变换已经推导结束了。
补充:
为什么我们将顶点(x,y,z)经过mvp之后,然后会除以第四维度的分量呢?原因是变换之后的点映射到规范化域内,也就是ndc空间。

http://www.codeguru.com/cpp/misc/misc/graphics/article.php/c10123/Deriving-Projection-Matrices.htm#page-3
http://blog.csdn.net/zhanghua1816/article/details/23121735
在3D图形学中所有的变换,其中透视变换是稍微复杂一点的。平移变换和缩放变换很容易明白。而旋转变换只要你能够明白基本的三角学也是可以很容易的推导出来的。如果你之前看过这个矩阵,你也许不是很直观地看出他是怎么来的。下面就是作者自己的推导过程喽!!!
对于刚接触图形学的新手来说,图形学是不是需要有很深厚的数学知识呢?其实也不必要有如此的畏惧。本文尽量从理解的角度来写,都是很简单易懂的推导。
1、什么是透视
计算机的显示器是二维的,而你想要将3D的东西展示成一张图片,就需要将3D几何物体通过一种方式转换为2D图片。这就是透视矩阵要做的事情。其中一种简单的透视方法就是忽略z轴,只用x和y坐标。

当然,这个方法简单,但是却不常用。对于初学者来说,不会将透视投到一个平面上。而将你的几何体投射到一个新的体内。这个体称为规范化视域体。对于不同的api来说,对于规范化视域体内的坐标是不同的。在D3D中,我们将这个规范化视域体扩展为(-1,-1,0)to(1,1,1)。当你的顶点被映射到规范化视域体内之后,只用到了点的x和y坐标,它被映射到屏幕上去。z坐标没有用处,但是z坐标在深度检测中会被用到。
上图中,使用的是左手坐标系,这也是D3D中使用的坐标系。这篇文章呢,也是用的是左手坐标系。
2、正交投影
正交投影有一个特点,就是所有的透视线和投影平面是垂直的。下图中会看到规范化视域体。

如上图,左下角是(-1,-1,0)而右上角是(1,1,1)。
如上图,你可以看到视锥体是通过6个平面限定的。
left:x = l
right:x = r
bottom:y = b
top:y = t
near:z = n
far:z = f
正交变换的特点是3D物体在空间中经过投影到平面上之后,保持大小相同。
三个坐标轴分别考虑怎么映射。这个涉及到从原始的视域体映射到规范化的视域体呢。下面我们已x轴为例子,看看如何从[l,r]映射到[-1,1]的范围内。
原始视域体内x的范围是:
l<=x<=r
将其两边同时减去l得到:
0<=x-l<=r-l
然后,不等式两边再同时除以r-l,这个值是你的视域体的宽度。
0<=(x-l)/(r-l)<=1
然后再乘以2,得到:
0<=2(x-l)/(r-l)<=2
然后再减去1
-1<=2(x-l)/(r-l) - 1<=1
然后得到:
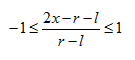
然后我们改写中间的项,写成px+q形式:
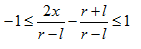
中间的就是用来将原始视域体内的点映射成规范化视域体内的点。

同样的对于y也是类似的映射方式,其结果为:

最后你需要把z轴也做映射。映射的范围是[0,1],而不是[-1,1]。
n<=z<=f
两边同时减去n得到:
0<=z-n<=f-n
然后两边再同时除以f-n,得到:
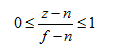
然后也写成pz+q的形式:
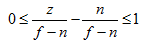
然后z即为:

这样我们就得到了,如下的等式:

写成矩阵的形式为:
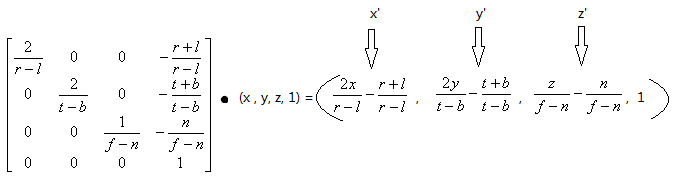
然后我们可以简化上面的矩阵,仅仅使用视域体的宽度和高度来改写,并且让r=-l,t=-b,那么
矩阵可以简化为:

然后我们再将这个矩阵,改写成一个缩放矩阵和一个平移矩阵的乘积:
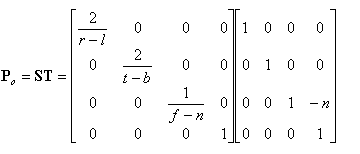
首先,将原始视锥体的近平面作为原点,即作为一个z轴的平移,所以使用平移矩阵。然后再将点映射到规范视锥体内,所以使用了一个缩放矩阵。
这个就得到正交投影矩阵了。
3、透视投影
透视投影与正交投影的不同点在于,透视投影的视锥体是一个削去尖的椎体,如下图所示:

利用相似三角形来推导透视之后的点:

上图中L的距离等于:

然后我们因为L2这个线段与z轴的交点是在近平面上的,所以其z坐标为n;另外因为L的与z轴的交点的z坐标为就为z,那么根据相似三角形的知识可以知道L2的长度:

进一步的改写:
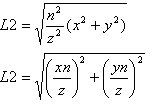
可以知道(x,y,z)经过透视之后得到的坐标为:
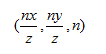
此时,回想上面的正交投影透视点(x,y,z)被映射到规范化视域体内的公式:

这里看到x和y的公式,那么此时我们把这里的x和y更换成nx/z,以及ny/z即可得到:
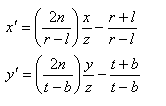
接着,对于上面的式子,两边同时乘以z之后得到:
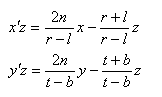
此时有了两个等式,我们还得往矩阵的上靠靠。如何将等式写成如下的形式:

这有写成这样的形式,才能方便改写为矩阵的形式。
注意此时我们得到了两个如下的等式:

如果再有一个z’z的等式,那么我们就得到了如下的:

这里构建如下的等式:
z’z = pz + q
其中,p和q是常量。
我们知道当z’=0时,z=n。当z’=1,z=f。代入上面的式子,可以求出p和q的值:

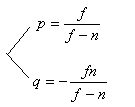
于是我们有了如下的式子:

此时我们有了3个式子:
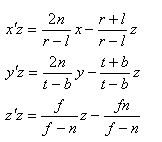
之前我们的4维矩阵最后一行永远是(0,0,0,1)所以w’=1,那么两边同时乘以z,得到:
w’z = z.
此时我们有了如下的四个式子:
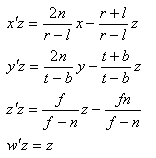
然后我们改写成矩阵的形式:
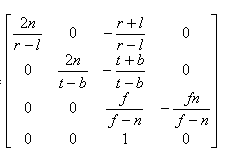
此时简化矩阵,令r=-l,t=-b,然后w表示r-l;h=t-b,得到简化的矩阵为:
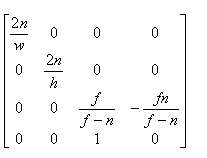
问题到这里已经基本解决了,最后我们的简化是与视域体的张角有关系,也很简单,如下图所示:

其中:

我们再次设定w/h,即视域体的宽高比为r。w为视域提的宽度,即r-l。h为视域体的高度,即t-b。
那么矩阵中的2n/w=2n/rh。
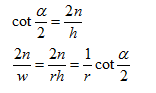
于是我们的矩阵简化为:

到这里我们的透视变换已经推导结束了。
补充:
为什么我们将顶点(x,y,z)经过mvp之后,然后会除以第四维度的分量呢?原因是变换之后的点映射到规范化域内,也就是ndc空间。

相关文章推荐
- 透视变换的原理推导(cvGetPerspectiveTransform)
- Planar Shadow中Shadow Matrix的推导
- 语法树和推导
- 今天竟然忘记了余弦公式和点积公式的互相推导关系了。
- 分数延迟的原理推导
- 模板函数中指针作为调用参数时模板参数的推导问题
- OpenGL Projection Matrix(投影矩阵推导)
- 一个通用的makefile写法,自动推导文件的依赖关系
- 可推导出幂律分布的模型的文献小结
- Flash/Flex学习笔记(51):3维旋转与透视变换(PerspectiveProjection)
- 西方有术傅里叶 (离散傅里叶变换的推导(1))
- 算法复杂度的差分方程推导3(两种一般情况的兼容)
- 基本的2D图形变换&变换矩阵推导(转)
- 坐标旋转变换公式的推导
- 推导全部勾股数方法(转)
- 二叉树遍历推导的一点思考
- 欧拉函数的推导
- Traits 编程技法+模板偏特化+template参数推导+内嵌型别编程技巧
- Oracle中的位运算以及推导公式
- 透视投影的推导
