有限元方法的核心思想是什么？

有限元方法的核心思想是什么？

有限元方法似乎是在不断地简化着什么。

请问有限元方法的核心思想是什么？在哪些层面对方程做了简化？每一次简化的依据和思路是什么？

2 条评论

按投票排序按时间排序

31 个回答

菲兹睡眠厌倦患者
138 人赞同

有限元法（Finite Element Method）是基于近代计算机的快速发展而发展起来的一种近似数值方法, 用来解决力学，数学中的带有特定边界条件的偏微分方程问题（PDE）。而这些偏微分方程是工程实践中常见的固体力学和流体力学问题的基础。有限元和计算机发展共同构成了现代计算力学 （Computational Mechanics）的基础。有限元法的核心思想是“数值近似”和“离散化”，
所以它在历史上的发展也是围绕着这两个点进行的。
“数值近似”

由于在有限元法被发明之前，所有的力学问题和工程问题中出现的偏微分方程只能依靠单纯的解析解（Analytical Solution）得到解答。这种方法对数学要求很高，而且非常依赖于一些理想化的假定（Assumption）。比如在土木工程中梁柱计算中出现的平截面假定，小应变假定，理想塑性假定。这些假定其实是和实际工程问题有很大偏差的，而且一旦工程问题稍微复杂一些我们就不能直接得到解析解，或者解析解的答案误差过大。而有限元法把复杂的整体结构离散到有限个单元（Finite Element），再把这种理想化的假定和力学控制方程施加于结构内部的每一个单元，然后通过单元分析组装得到结构总刚度方程，再通过边界条件和其他约束解得结构总反应。总结构内部每个单元的反应可以随后通过总反应的一一映射得到，这样就可以避免直接建立复杂结构的力学和数学模型了。其总过程可以描述为：
总结构离散化 — 单元力学分析 — 单元组装 — 总结构分析 — 施加边界条件 — 得到结构总反应 — 结构内部某单元的反应分析

在进行单元分析和单元内部反应分析的时候，形函数插值（shape function interpolation）和
高斯数值积分（Gaussian Quadrature）被用来近似表达单元内部任意一点的反应，这就是有限元数值近似的重要体现。一般来说，形函数阶数越高，近似精度也就越高，但其要求的单元控制点数量和高斯积分点数量也更多。另外单元划分的越精细，其近似结果也更加精确。但是以上两种提高有限元精度的代价就是计算量几何倍数增加。

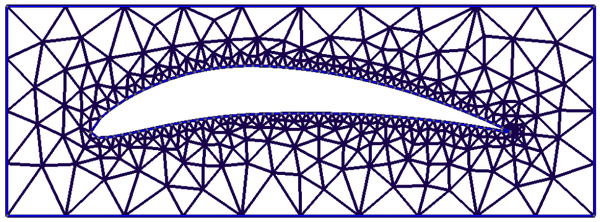
为了提高数值近似精度同时尽量较少地提高计算量，有限元法经历了很多发展和改良。下图就是一典型的有限元问题，因为模型中间空洞部分几何不规则性，结构用有限三角单元划分。由于在靠外区域，结构反应变化程度不是很大，因此划分的单元比较大和粗糙，而在内部，应力变化比较大，划分也比较精细。而在左边单元划分最密区域，有应力集中现象（如裂纹问题的奇异解现象），所以又有相应的高级理论（比如non-local theory）来指导这部分的单元应力应变计算。结构被选择性地离散，和高级理论构成了有限元发展的主要研究方向。



2. “离散化”

离散化和相应单元特性和收敛研究也是有限元中一个重要研究领域，总的来说，有限单元和他们组装成的总体结构主要分为：
1-D 单元 (1-D element)

杆单元 (bar element) ------ 桁架 (truss)

梁单元 (beam element) ------ 框架 (frame)

板单元 (plate element) ------ 壳体 (shell)
2-D单元 (2-D element) ------ 平面应力体 (plain stress) 和 平面应变体 (plain strain)

三角单元 (triangle element)

四边形单元 (quadrilateral element)

多边形单元 (polygonal element)
3-D 单元 (3-D element) ----- 立体结构 (3-D problem)

三角体 (tetrahedrons element)

立方体单元 (hexahedrons element)

多边体单元 (polyhedrons element)

具体的分类和单元形状见下图

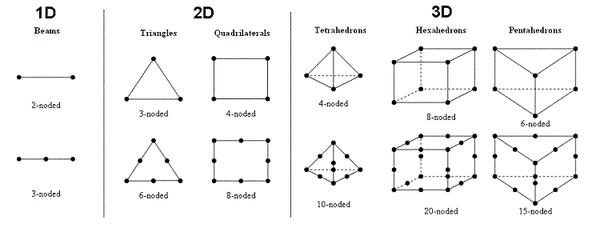
可以看到每种单元又可以提高形函数的阶数（控制点 node 数量）来提高精度。很多有限元研究也集中在这个领域。比如研究新的单元引用于结构动力反应以减小数值震荡，比如用3-D单元去模拟梁单元等等。其实理论上来说这个领域可以有无限可能，因为对精度和数值稳定的追求可以是无限的。

3. “光滑边界” 和 与CAD的交互问题

其实这个算不上有限元的核心思想，不过是现在有限元研究热的不能再热的领域了，就是Hughes提出的“NURBS”有限元法，它的原理是用空间样条曲线来划分单元。如第一幅图所示，传统的有限元在处理不规则边界的时候一般都是较多的单元和用三角单元，多边形单元来解决，而且单元控制点都是和单元在一个平面上。 而NURBS 单元的控制点脱离了单元本身，并且利用B-spline理论上可以把单元的光滑程度（continuity）提高到无限，而且不会显著提高计算量。



发展NURBS的另外一个好处是，在建模中常用的CAD软件是用B-spline来进行模型建立基础的，而NURBS 正好也是用用B-spline作为basis。 所以CAD和NURBS的交互可以非常简单和高效的，甚至可以说是无缝连接。因此在工业界中十分复杂的模型都可以用CAD进行建模，再用NURBS进行有限元计算，如下图。现在成吨的有限元paper都来自这个领域，因为有限元的基本理论基本已经成熟和robust，利用高性能计算机进行大尺度（large-scale）和高复杂结构模拟也是有限元发展的一个主要方向。



P.S. ：需要提到一点的是，没有高性能计算机技术的大力发展，就不可能有有限元的发展。有限元的理论最早是出现在1960年代，直到1970之后才随着计算机的发展而迅速发展。而现在发展迅速的计算力学也是得益于高性能计算机的发展。可能当某一天计算机处理速度可以强大到我们可以用最复杂，最密集的单元完美快速地模拟任意结构，我们也不用再操心精度问题了。 所以我觉得有限元的核心还需要加上计算机技术的发展吧。

编辑于 2015-09-197
条评论感谢

收藏•没有帮助•举报•作者保留权利


计算力学
45 人赞同

简单的来说，有限元的核心一是求PDE(偏微分方程)的近似解，二是离散化(discretization)。

首先谈下第一个核心。很多问题都可以归结为一个泛函数(functional)。例如弹性力学中，可以写出一个泛函数表示势能。然后解决问题的方式便可以归结于find a function to minimize the functional, 即找出一个函数去最小化泛函数，就像之前有人回答的最小势能原理。想要找到这个函数，就需要用到变分法(variational method),即令泛函数的一阶变分等于零。这个原理类似于找一个函数的极值是通过令它的导数等于零来求出的。一阶变分等于零这个等式通过分部积分后通常可分为两个部分，一个是governing
equation,即偏微分方程(PDE)形式的控制方程，另一部分是边界条件(boundary condition)。于是问题便转化为了求解带有边界条件的PDE。工程中通常希望用简化的方法求解PDE的近似解。近似求解PDE有多种方法，比如Strong form Galerkin, Weak form Galerkin, Rayleigh Ritz method。他们的核心思想都是设一个形式已知的近似方程(approximation function)(有限元中常用多项式(polynomial)), 然后带入原PDE或functional来求解unknown
coefficients。例如设近似方程为

。

就是要求的unknown coefficients,而

是basis
function,形式是自己设的，所以是已知的。当然，近似方程需要满足一些条件，如满足边界条件，不能跳项等。由于Strong form Galerkin的近似方程需要满足所有边界条件(包括essential和natural),而Weak form和Rayleigh Ritz只需满足essential boundary condition,所以有限元通常使用后两种求解方法。关于边界条件的划分和近似求解PDE的具体方法如果需要我可以再日后补充。

第二个核心是离散化。一个连续的介质会被离散成数个简单的基本几何单元,即element。这些elements是通过节点(nodes)相互联系。这个过程就是通常所说的网格划分(mesh)。对于每一个element都可以用上一段的方法进行求解，然后通过节点间的联系将element的结果组合成整个domain的结果，即assemble the stiffness matrix。

P.S. 由于这门课是国外学的，有些名词不确定中文的准确翻译，所以用英文注释了。有些实在不知道怎么翻的就直接用英文了，还请谅解，希望回答对您有帮助！

编辑于 2016-03-2713
条评论感谢

收藏•没有帮助•举报•禁止转载



周肖飞藏獒，肩章，渐近线三者之间有什么联系？
25 人赞同

谢@Ch’enMeng邀

从邀请之日我就在思考这个问题了，但最近实在太忙，懒癌又作祟，因此拖了这么久，题主提了个好大的问题，@Ch’enMeng又表现的那么谦虚，都让我不敢下手了，等了这么久，也没有人添加一份答案，我就写点自己浅薄的理解吧

从模型简化的角度来看，有限元的所有结构单元（structure element）基本上都基于材料力学的基本假设，比如杆是均匀的，梁是遵守平行界面假设的，我们平时虽然说有限元的最终目的是结构的优化，但原始计算结果却是节点的受力（严格的说是节点的位移U），因此，有限元的计算其实和材料力学是相同的道理，如果我们将模型按照截面法进行分离，分离到最原始的元素也就是我们的单元。下图所示的变截面杆，如果我们按照材料力学的方法计算，无非是在变截面处进行分割，如果按照有限元，也是在变截面处划分成两个单元。


但是，材料力学在进行计算时需要的简化太严格，无法在复杂的结构中应用（比如上述的杆件有好多个截面和材料呢）。在有限元中，基本的单元其实就是材料力学的基本构件，单纯的材料，规则的几何外形等等，这些假设在单元足够小的前提下是成立的，但当组装成复杂结构后，过小的单元又会带来数值计算上的误差放大。

从数学计算的角度来看，有限元由于其数值方法的本性，在计算中需要做大量的简化，比如，计算机无法像牛顿-莱布尼兹那样寻找原函数来积分，只能采用数值积分方法，这就会带来误差，还比如解方程所需要的迭代等等，就像@Ch’enMeng所说的，有限元是一种工程方法，我们大多数时候更需要的是一个稳定的解。

所以，在对模型进行网格划分的时候，并不是单元越小越好，也不是所有单元采用实体就更好，很多时候，我觉得采用结构单元更有效（比如现在主流的桥梁分析软件都是基于梁的，没有实体单元），那简化的原则是什么呢，就是看它的受力，如果是杆的受力特点，就简化为杆，如果是杆件又承受弯曲了呢，那就简化为梁，如果结构无法简化成杆，梁，壳的时候，那就用实体。

发布于 2015-02-092
条评论感谢

收藏•没有帮助•举报•作者保留权利


工程师. 教师.
7 人赞同

有限元方法的核心思想，从最初创立理论的大学问家，到今天的教授，到应用方面的工程师，理解是大不相同的。这个问题的答案可以有很多种。比如每一本有限元教科书的前言都会谈到那个作者本人的理解。

从一个工程师的角度看，有限元方法是将一个真实的工程问题，比如桥梁，楼房，机械，汽车，等等，和一个等效的可以进行计算的模型对应起来，或者说是一种建立数学模型的方法。这个数学模型包括了原结构的几何，材料，荷载，约束，等等对等数据。

一个好的工程师应该了解有限元的历史，理论等。所有的理论归根到底是“等效”的意义是什么？怎么就算等效了？为什么网格越小，等效性就越好？即所谓“收敛性”。

但是对工程师来说，更重要的是，你的数学模型和物理实体是怎样对应的。简化的根据是什么？引入误差的原因是什么？求解器的限制是什么？你往往需要有几个解析解在手上随时对照，校验你的建模方法是否有效。而且你要不断地和试验结果对比。

编辑于 2015-08-131
条评论感谢

收藏•没有帮助•举报•作者保留权利


学习，思考，理解，改善。
2 人赞同

1965年冯康在《应用数学与计算数学》上发表的论文《基于变分原理的差分格式》，是中国独立于西方系统地创始了有限元法的标志。

－－冯康（中科院院士、数学家）

发布于 2015-06-07添加评论感谢

收藏•没有帮助•举报•作者保留权利



Leny科学计算学习者，毕竟不是程序猿。
21 人赞同

Thomas Hughes 镇楼！


相比较已有答案而言，我的回答偏数学一点，既然题主问了“每一步的依据是什么”，那么要回答清楚就必须要用严谨的数学语言。

以2D的传热问题为例。傅立叶定律表述为

其中q是heat flux, kappa是conductivity matrix，u是温度。对于一个二维的域（大写omega表示），函数f作用在整个域上（理解为载荷）。我们的问题是给定了载荷，已知边界上某些点的heat flux, 以及另一些点上的温度，求整个域上各个点的温度。

用数学语言来描述就是：

已知f, g, h, 求u 使得

第一个方程里f是外界载荷，是给定的，在传热问题中就是热源了，定义域是整个域，用大写omega表示；第二个方程的定义域是

,意思是在

上的点的温度是已知的；第三个方程的定义域是

，意思是在这个

上的点的heat
flux是已知的。

这个表述方式叫做strong form，记作<S>。接下来介绍问题的weak form，记作<W>，数学上可以证明<S>和<W>是完全等价的。证明不难，主要技术是散度定理和分步积分，但为省事我就不写出来了。

首先引入两个空间，一个叫trial solution space用小写delta表示，一个叫variation space用V表示，trial solution space里的函数都满足u = g on


,也就是我们要求的解；variation space里的函数都满足 u = 0 on


。那么<W>的表述是这样的：

给定f,g,h,求u属于

使得对于所有的w属于V都有



如果令


那么<W>就可以写作


为什么要搞出个weak form来？它的意义在于引入了两个空间，然后说对于这个空间里的所有函数都必须满足这个式子。那么自然我们就可以像线性代数里一样选定一组“基底”来表示这个空间了。

到目前为止我们没有对问题进行近似，接下来是网格的登场，用

作为原本

的近似。把将要求的u分解为v和g ,

,v属于variation
space g属于trial space. 那么问题就可以改写为：

这叫作Glerkin form,记作<G>

注意从<W>到<G>是一种近似，近似在我们将原本的域离散成了多个元素的组合。

接下来是shape function的引入，shape function有n（节点数）个， 用N(x)表示，它们的作用在于插值表示其它非节点处的值。这些函数有个特点就是“作用范围”很小，它们只在节点周围的若干个element上有值，其它地方一概为0。这样设计的意义重大，就是我们可以真正从element的角度考虑问题，再将多个element组合起来。有了shape function之后，问题就可以写为


,



d是节点上的值，未知；N是shape function是已知的 g h都是已知的，至此问题其实就变成了

Kd = F 了， 在力学中，K可以称为刚度矩阵，F称为外力，d是形变。 我们把这个叫作 Matrix Form,记作<M>。 实际操作中，K和F都是通过先写出每个element的k 和 f再进行组装。得到全局的K, F之后剩下的事情就是解这个方程。虽然这个矩阵通常很大，但是shape function以及其它一些因素决定了它是稀疏矩阵，于是可以用一些已有的数学方法求解。

总结一下，对于有限元问题，我们首先用strong form描述问题，然后通过引入trial solution space和variation space推导出weak form，二者等价；接着进行离散得到Glerkin form，这一步有近似；最后通过形函数得到矩阵形式。



关键技术是将问题离散化、形函数插值。整个方法的核心是保证<W>中对

的积分不变。

写完之后自己读一遍，我确信如果读者没有系统学习过有限元理论是完全看不懂的。但是想真正理解有限元，还是需要从理论学起。推荐图中的书。

编辑于 2015-04-1111
条评论感谢

收藏•没有帮助•举报•作者保留权利



27 人赞同

发现很多人对有限元的理解并不是特别深刻。有限元只是求解偏微分方程的一种数值方法而已。所以理解有限元你必须要反思你学过的数值方法，比如数值分析的时候你是如何近似一个函数的，如何近似积分，近似导数？？我们会发现数值方法的核心是 空间内的一组基来近似 空间内的复杂形式。简单说就是利用 一组简单的表达式来近似任何复杂的形式。拉格朗日插值不就是采用非常简单的基函数来形成的。数值积分我们都是划归到了对多项式的积分上。。。。

理解了数值方法的核心再理解有限元就简单多了，有限元求解的对象是偏微分方程。考虑偏微分方程，最终的解的定义域是在一个区域内的，这个区域内的解析表达式是非常困难的。这时候理所当然大家就会考虑怎么求解这个问题呢？肯定是在这个区域内找一些简单函数去近似拟合，比如利用多项式 利用周期函数等等。。。。但是在这样求解的过程中又会发现，我们在整个区域内近似是非常困难的，对于很多问题还是不是那么容易求解，试想一个形状非常不规则的区域？？？这时候，科学家就会萌生了能否我把整个区域的问题划分成一系列的简单区域，简单区域上问题求解是非常简单的，最终的结果把所有区域结合起来不就可以了吗？
这时候科学家又会联系到，结构力学中的杆件结构，因为在杆件结构中已经有了这样的方法。所以经过一系列的推导就有了这样分片求解问题的方法 即有限元方法。

有限元并没有什么复杂的，楼主也不要被什么最小势能，变分原理吓住，因为这些都是在逐步完善有限元方法过程中理论的完善，最小势能，变分原理是为了建立有限元的弱形式，或许你会问 弱形式是什么呢？ 举个例子，如果我们分析的微分方程式二阶的，也就是方程中含有关于自变量的二阶导数，那么我们建立的近似函数是不是也要具有二阶呢？答案是肯定的，事实证明，阶段太高是非常不利于问题求解的，那么就会思考可不可有一种等效的形式，但是阶次又是比较低的？当然有了，这就是弱形式，试想如果可以用一次函数去近似是不是非常简单呢？不得不说这是有限元方法得以这么盛行的非常重要的理论基础。