图像处理之让手心长出眼睛,其实嘴也可以
2016-07-04 10:05
330 查看
无图像,不处理,先上效果图。手上长嘴当然也可以,不过感觉有点恶心 ~ 就不上那种图了。
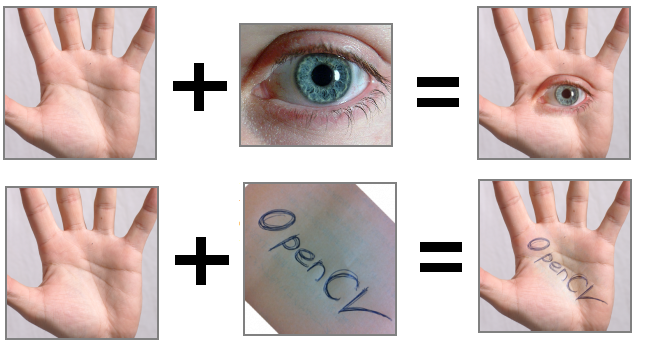
这里所采用的算法就是大名鼎鼎的泊松融合算法,它的应用非常广泛,除了上面这种手上长眼睛的效果,还可以实现“纹理拼接”、“精细抠图”、“移花接木”等等效果。我之前已经从纯数学的角度讨论过它的原理了。
但是,当初给出的代码仅仅是为了算法演示的目的,所以并未进行优化。可以说是最简单、最原始的实现方法。然后,我写完就扔一边很久没碰了。今天有朋友向我了解,我表示印象中用高斯法解大稀疏矩阵也可以实现对泊松方程的求解,但是当初没有深究。今天好奇心再次被唤起,想来再续前缘。没想到一顿翻箱倒柜,还真找到些不错的资料。其中一篇感性角度理解该算法的文章感觉很不错。不仅介绍了算法的原理(而且完全不从数学角度,就从感性认识谈也一样深刻),还谈及了优化的实现方法。今天我特别二次加工后与各位分享。
原文链接:http://eric-yuan.me/poisson-blending/
下面的图基本都是盗的原文中的,原文是英文,我根据自己的理解翻译+改编,希望能融合一些我个人的理解。
首先,让我们从最最简单的“一维”情况开始考虑。如下图所示,我们的目标是将左图中红色的部分copy到右图中,这个时候左图中红色部分就相当于是最开始图中的“眼睛”,右图就是一个手掌。
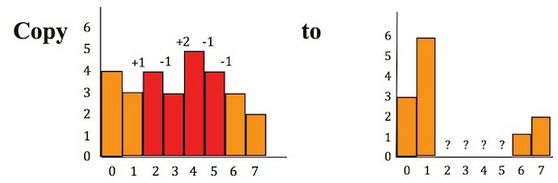
如果要做到天衣无缝,我们应该保证哪些条件?这个我在过去的文章中讨论过,总而言之,言而总之,就两条:1)将眼睛融入手掌之后,眼睛和手掌相连的边缘过渡要平滑(用图像处理的术语说,就是梯度小)。2)眼睛内部的自身纹理要最大程度保留,不能融合之后眼睛没了,就剩手掌那肯定不行。
就我们当前所面对的这个例子,其实就是要求:
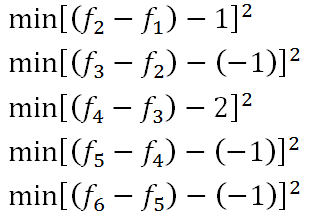
其中f 是右图中的“信号”,而+1、-1、+2、-1、-1是原图(左图)本来的梯度。那我们有没有什么是已知的呢?有的!f1=6,f6=1,即融合边界的信息我们已知。于是化简有
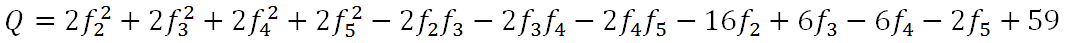
然后根据费马定理,当有极值时,偏导数等于零,即
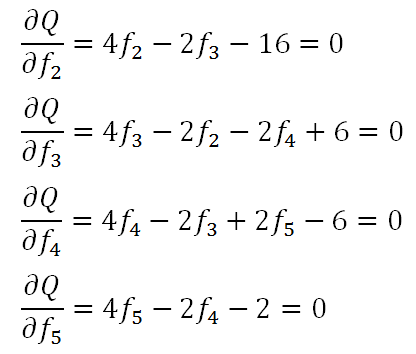
然后如果用矩阵形式来表示方程组便有
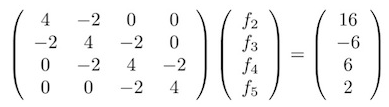
现在要解一个线性方程组,而且这个方程组还是稀疏的,显然用高斯-塞德尔迭代法是非常不错的选择,这也是泊松方法的原作者最初使用的求解方法。而且高斯法会比雅各比法快很多。更多高斯-塞德尔迭代法的内容请见
/baimafujinji/article/details/50582462
然后我们咔嚓一顿狂解,最后得到方程组的结为:f2=6,f3=4,f4=5,f5=3,这好像并不太直观,于是用图形来表示
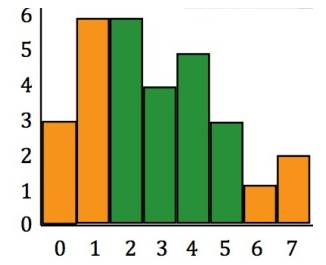
哈啊!看出门道了吗?首先,接合的地方过渡很自然(梯度小),内部纹理保持的也不错(基本和原图一致)。Yes, we get it!
然后呢?我们既然处理的对象是图像,所以还得回到二维的情况来看看。其实,你应该理解,这个推广的过程其实没啥新鲜的东西。但它与你编程实现直接相关。下图演示了我们将要开展的工作。数字方格是我要copy过来的像素点,红色表示接合边缘。

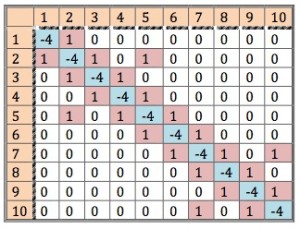
跟一维的情况一样,我们现在要解线性方程组 Ax = b,其中A是一个N×N的方阵,N是我们要copy的像素数目,本题中N=10。我们用下面的伪代码演示了创建一个所需的10×10方阵。
在方程组 Ax = b中,b 是一个N元向量,它是由下面这个式子创建的
其中G(·)是求梯度,散度由下面公式求得(这属于经典离散数值解,不做过多解释,如果你感觉困惑可以看我前面的文章,已经说得很详细了)
div G = -4 f(x,y) + f(x-1,y) + f(x,y-1) + f(x+1,y) + f(x,y+1)
其中i的邻域(Neighbor)指的是i的四邻域点中属于边界的部分,例如从图中可以看出
Neighbor(pixel 1) 有三个点: left, up, right;
Neighbor(pixel 8) 有两个点: left, up;
Neighbor(pixel 5) 有一个点: up.
这里我还想根据Patrick的经典论文之原文来对上面的结论做进一步的解释。其中,p是S中的一个元素,Np是点p位于S内部的4邻域点。<p,q>表示一个点对,其中q∈Np。Ω的边界
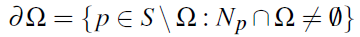
请注意,S和Ω的所代表的意思我在前面的文章中已经给出,请读者参考之前的文章。令fp 代表p点处的f值。那么原来的优化问题就变成了如下的离散形式:
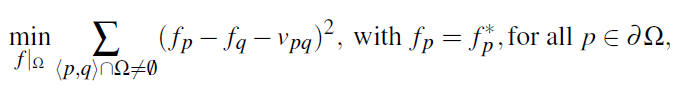
vpq 是v((q+p)/2)在边[p,q]方向上的投影,即

上述最优化问题的解满足
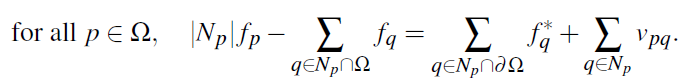
(7)
这就是我们上面给出的那个公式。对于位于S中的Ω的边界像素点p,|Np|<4,即边界上点的邻域点少于4个,显然边界上的点p至少有一个邻域点位于Ω内部。然而,对于那些位于Ω内部的像素点p而言,即Np∈Ω,等式右端的边界项就不复存在了,即有
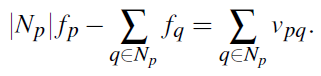
方程(7)是一个很大的稀疏矩阵,所以可以用经典的迭代法进行求解。作者指出他原文中的结果是采用高斯-塞德尔法得到的。
如果我们知道矩阵 A 和向量 b, 我们就可以根据x = A-1 * b来计算向量x,这也就是目标图像中要被填充的部分像素。

这里所采用的算法就是大名鼎鼎的泊松融合算法,它的应用非常广泛,除了上面这种手上长眼睛的效果,还可以实现“纹理拼接”、“精细抠图”、“移花接木”等等效果。我之前已经从纯数学的角度讨论过它的原理了。
原文链接:http://eric-yuan.me/poisson-blending/
下面的图基本都是盗的原文中的,原文是英文,我根据自己的理解翻译+改编,希望能融合一些我个人的理解。
首先,让我们从最最简单的“一维”情况开始考虑。如下图所示,我们的目标是将左图中红色的部分copy到右图中,这个时候左图中红色部分就相当于是最开始图中的“眼睛”,右图就是一个手掌。

如果要做到天衣无缝,我们应该保证哪些条件?这个我在过去的文章中讨论过,总而言之,言而总之,就两条:1)将眼睛融入手掌之后,眼睛和手掌相连的边缘过渡要平滑(用图像处理的术语说,就是梯度小)。2)眼睛内部的自身纹理要最大程度保留,不能融合之后眼睛没了,就剩手掌那肯定不行。
就我们当前所面对的这个例子,其实就是要求:
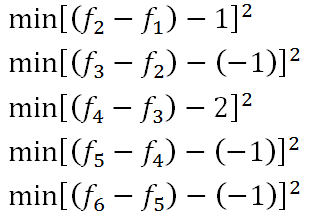
其中f 是右图中的“信号”,而+1、-1、+2、-1、-1是原图(左图)本来的梯度。那我们有没有什么是已知的呢?有的!f1=6,f6=1,即融合边界的信息我们已知。于是化简有
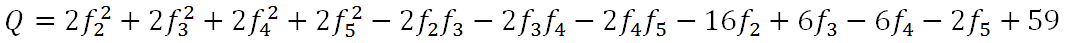
然后根据费马定理,当有极值时,偏导数等于零,即
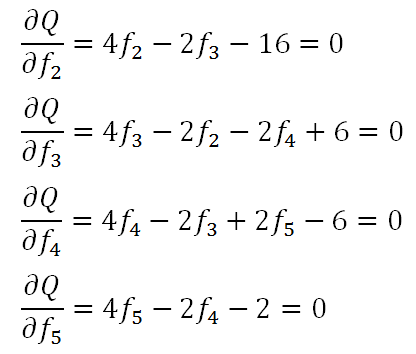
然后如果用矩阵形式来表示方程组便有
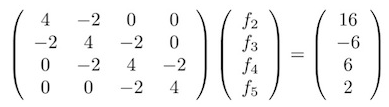
现在要解一个线性方程组,而且这个方程组还是稀疏的,显然用高斯-塞德尔迭代法是非常不错的选择,这也是泊松方法的原作者最初使用的求解方法。而且高斯法会比雅各比法快很多。更多高斯-塞德尔迭代法的内容请见
Jacobi迭代法与Gauss-Seidel迭代法 _一九八网络科技V客学院-IT技术博客
/baimafujinji/article/details/50582462然后我们咔嚓一顿狂解,最后得到方程组的结为:f2=6,f3=4,f4=5,f5=3,这好像并不太直观,于是用图形来表示

哈啊!看出门道了吗?首先,接合的地方过渡很自然(梯度小),内部纹理保持的也不错(基本和原图一致)。Yes, we get it!
然后呢?我们既然处理的对象是图像,所以还得回到二维的情况来看看。其实,你应该理解,这个推广的过程其实没啥新鲜的东西。但它与你编程实现直接相关。下图演示了我们将要开展的工作。数字方格是我要copy过来的像素点,红色表示接合边缘。

跟一维的情况一样,我们现在要解线性方程组 Ax = b,其中A是一个N×N的方阵,N是我们要copy的像素数目,本题中N=10。我们用下面的伪代码演示了创建一个所需的10×10方阵。
for i=1:row number for j=1:col number if(i==j) matrix(i, j)=-4 elif(adjacent(pixel(j), pixel(i))) matrix(i, j)=1 else matrix(i, j)=0 end end end最终我们生成的矩阵应该是长成下面这个样子(我之前以为原博文作者这个地方写错了。直到我编码实现的时候才发现其中另有玄妙。真是实践出真知啊!在下一篇文章中,我会结合Matlab代码来演示这个地方。):

在方程组 Ax = b中,b 是一个N元向量,它是由下面这个式子创建的
b[i] = div ( G( Source(x,y) ) ) + Neighbor(target i) ; i=1..N
其中G(·)是求梯度,散度由下面公式求得(这属于经典离散数值解,不做过多解释,如果你感觉困惑可以看我前面的文章,已经说得很详细了)div G = -4 f(x,y) + f(x-1,y) + f(x,y-1) + f(x+1,y) + f(x,y+1)
其中i的邻域(Neighbor)指的是i的四邻域点中属于边界的部分,例如从图中可以看出
Neighbor(pixel 1) 有三个点: left, up, right;
Neighbor(pixel 8) 有两个点: left, up;
Neighbor(pixel 5) 有一个点: up.
这里我还想根据Patrick的经典论文之原文来对上面的结论做进一步的解释。其中,p是S中的一个元素,Np是点p位于S内部的4邻域点。<p,q>表示一个点对,其中q∈Np。Ω的边界
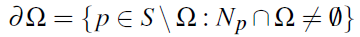
请注意,S和Ω的所代表的意思我在前面的文章中已经给出,请读者参考之前的文章。令fp 代表p点处的f值。那么原来的优化问题就变成了如下的离散形式:
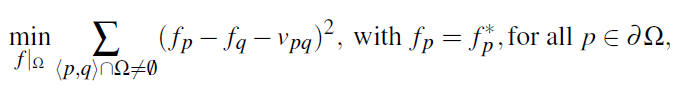
vpq 是v((q+p)/2)在边[p,q]方向上的投影,即

上述最优化问题的解满足
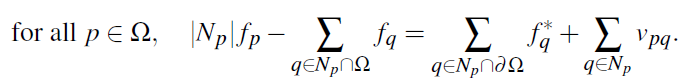
(7)
这就是我们上面给出的那个公式。对于位于S中的Ω的边界像素点p,|Np|<4,即边界上点的邻域点少于4个,显然边界上的点p至少有一个邻域点位于Ω内部。然而,对于那些位于Ω内部的像素点p而言,即Np∈Ω,等式右端的边界项就不复存在了,即有
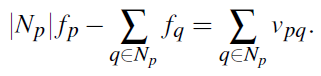
方程(7)是一个很大的稀疏矩阵,所以可以用经典的迭代法进行求解。作者指出他原文中的结果是采用高斯-塞德尔法得到的。
如果我们知道矩阵 A 和向量 b, 我们就可以根据x = A-1 * b来计算向量x,这也就是目标图像中要被填充的部分像素。
相关文章推荐
- java IO:java IO流总述
- Android中使用Handler造成内存泄露的分析和解决
- 经常访问的网站
- Android View系统源码分析(三)—— 根View内部消息派发过程&ViewGroup.dispatchTouchEvent()
- iOS多线程安全与性能分析
- 学前环境准备
- Java1.5 新特性 可变参数
- 第一个Java小程序
- Android中实现自定义的拍照应用
- Oracle常见的问题
- Python实现代码统计工具——终极加速篇
- Python之基础篇(三)
- python 匹配非英文字符 json.dumps函数原理
- hdu1616 深搜+简单回溯
- myBatis分页查询
- 怎样利用网络来赚钱
- 计蒜之道复赛F题 菜鸟物流的运输网络(网络流)
- 卡车更新问题
- 爬坑小记-Java里面的代码块讲解
- 每天学习一算法系列(5)(已知两个数组,数组里的元素有正有负,但是都是按照从小到大已经排好序,要求用尽可能小的时间复杂度编写一算法求出两个数组的最大交集)
