P=NP?

“P=NP?” 通常被认为是计算机科学最重要的问题。有一个叫 Clay Math 的研究所，甚至悬赏 100 万美元给解决它的人。可是我今天要告诉你的是，这个问题其实远远不是那么的重要。

我并不是第一个这样认为的人。在很早的时候，就有个数学家毫不客气的指出，P=NP? 是个愚蠢的问题，并且为了嘲笑这个问题，专门在4月1号写了一篇“论文”，称自己证明了 P=NP。我身边有一些非常聪明的人，他们基本也都不把这问题当回事。如果我对他们讲这些东西，恐怕已经是老生常谈，所以我只是在这里科普一下。

首先，你要先搞清楚什么是“P=NP?” 为此，你必须先了解一下什么是“算法复杂度”。为此，你又必须先了解什么是“算法”。

你可以简单的把“算法”想象成一台机器，就跟绞肉机似的。你给它一些“输入”，它就给你一些“输出”。比如，绞肉机的输入是肉末，输出是肉渣。牛的输入是草，输出是奶（或者牛米田共）。“加法器”的输入是两个整数，输出是这两个整数的和。“算法理论”所讨论的问题，就是如何设计这些机器，让它们更加有效的工作。就像是说如何培育出优质的奶牛，吃进相同数量的草，更快的产出更多的奶。

世界上的计算问题，都需要“算法”经过一定时间的工作（也叫“计算”），才能得到结果。计算所需要的时间，往往跟“输入”的大小有关系。如果你的牛吃了很多草，它就需要很长时间才能把它们都变成奶。这种草和奶的转换速度，通常被叫做“算法复杂度”。

算法复杂度通常被表示为一个函数 f(n)，其中 n 是输入的大小。比如，如果你的算法复杂度为 n^2，那么当输入10个东西的时候，它需要 100 个单元的时间才能完成计算。当输入 100 个东西的时候，它需要 10000 个单元的时间才能完成。当输入 1000 个数据的时候，它需要 1000000 个单元的时间。简单吧。

所谓的“P时间”，就是“Polynomial time”，多项式时间。简而言之，就是说这个复杂度函数 f(n) 是一个多项式。多项式你该知道是什么吧？不知道的话就翻一下中学数学课本。

“P=NP?”中的“P”，就是指所有这些复杂度为多项式的算法的“集合”，也就是“所有”的复杂度为多项式的算法。为了简要的描述以下的内容，我定义一些术语：

“f(n) 时间算法” = “能够在 f(n) 时间之内，解决某个问题的算法”

当 f(n) 是个多项式（比如 n^2）的时候，这就是“多项式时间算法”（P 时间算法）。当 f(n) 是个指数函数（比如 2^n）的时候，这就是“指数时间算法”（EXPTIME 算法）。了解一点复杂度理论，却又一知半解的人往往认为 NP 问题就是需要指数时间的问题，而 NP 跟 EXPTIME，其实是风马牛不相及的。很显然，P 不等于 EXPTIME，但是 P 是否等于 NP，却没有一个结论。

现在我来解释一下什么是 NP。通常的计算机，都是确定性（deterministic）的。它们在同一个时刻，只有一种行为。如果用程序来表示，那么它们遇到一个条件判断（分支）的时候，只能一次探索其中一条路径。比如：

if (x == 0) {

one();

} else {

two();

}

在这里，根据 x 的值是否为零，one() 和 two() 这两个操作，只有一个会发生。

然而，有人幻想出来一种机器，叫做“非确定性计算机”（nondeterministic computer），它可以同时运行这程序的两个分支，one() 和 two()。这有什么用处呢？它的用处就在于，当你不知道 x 的大小的时候，根据 one() 和 two() 是否“运行成功”，你可以推断出 x 是否为零。

这种非确定性的计算机，在“计算理论”里面叫做“非确定性图灵机”。与之相对的就是“确定性图灵机”，也就是通常所谓的“计算机”。其实，“图灵机”这名字在这里完全无关紧要。你只需要知道，非确定性的计算机，可以同时探索多种可能性。

这不是普通的“并行计算”，因为每当遇到一个分支点，非确定性计算机就会产生新的计算单元，用以同时探索这些路径。这机器就像有“分身术”一样。当这种分支点存在于循环（或者递归）里面的时候，它就会反复的产生新的计算单元，新的计算单元又产生更多的计算单元，就跟细胞分裂一样。一般的计算机都没有这种“超能力”。它们只能先探索一条路径，失败之后，再回过头来探索另外一条。所以，它们似乎要多花一些时间才能得到结果。

到这里，基本的概念都有了定义，于是我们可以圆满的给出 P 和 NP 的定义。P 和 NP 是这样两个“问题的集合”：

P = “确定性计算机”能够在“多项式时间”解决的所有问题

NP = “非确定性计算机”能够在“多项式时间”解决的所有问题

（注意它们的区别，仅在于“确定性”或者是“非确定性”。）

定义完毕。现在回到对“P=NP?”问题的讨论。

“P=NP?”问题的目标，就是想要知道 P 和 NP 这两个集合是否相等。为了证明两个集合（A 和 B）相等，一般都要证明两个方向：

A 包含 B

B 包含 A

你也许已经看出来了，NP 肯定包含了 P。因为任何一个非确定性机器，都能被当成一个确定性的机器来用。你只要不使用它的“超能力”，在每个分支点只探索一条路径就行。所以“P=NP?”问题的关键，就在于 P 是否也包含了 NP。也就是说，如果只使用确定性计算机，能否在多项式时间之内，解决所有非确定性计算机能在多项式时间内解决的问题。

我们来细看一下什么是多项式时间（Polynomial time）。我们都知道，n^2 是多项式，n^1000000 也是多项式。多项式与多项式之间，却有天壤之别。把解决问题所需要的时间，用“多项式”这么笼统的概念来描述，其实是非常不准确的做法。在实际的大规模应用中，n^2 的算法都嫌慢。能找到“多项式时间”的算法，根本不能说明任何问题。

对此，理论家们喜欢说，就算再大的多项式(比如 n^1000000)，也不能和再小的指数函数（比如 1.0001^n）相比。因为总是“存在”一个 M，当 n > M 的时候，1.0001^n 会超过 n^1000000。可是问题的关键，往往不在于 M 的“存在”，而在于 它的“大小”。如果你的输入必须达到天文数字才能让指数函数超过多项式的话，那么还不如就用指数复杂度的算法。所以，“P=NP?”这问题的错误就在于，它并没有针对我们的实际需要，而是首先假设了我们有“无穷大”的输入，有“无穷多”的时间和耐心，可以让多项式时间的算法“最终”得到优势。“无穷”和“最终”，就是理论家们的杀手锏。

为了显示这个问题，我们可以画一个坐标曲线，来比较一下 n^1000000 与 2^n，并且解出它们相等时的 n。我不用 1.0001^n 来比，免得有人说我不公平。我喜欢偷懒，经常用 Mathematica 来解决这些算式。下面就是我用它得出的结果和曲线图：



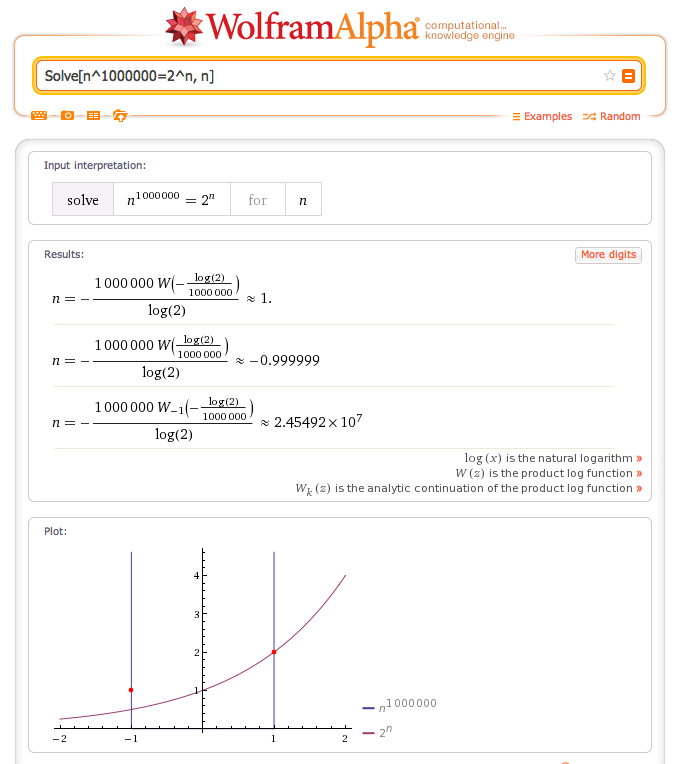
你看到了，当 1 < n < 24549200 的时候，我们都有 2^n < n^1000000 （n^1000000 那根曲线，一旦超过1就冲上天去了）。 所以只要输入没有达到2千万这个量级，2^n 的算法都比 n^1000000 的算法快。

n^1000000 也许不说明问题，但是“多项式”的范围实在太大了。n^(10^100) ，n^(10^(10^100))，…… 都是多项式。实际上，只要 c 是个常数，任何常数，n^c 就是个多项式。

当你抓住这个要害的时候，理论家们往往又说，你给的这个例子太离谱了，解决了“P=NP?”，能够帮助我们找到“快速”的多项式算法。这其实是一个偷换概念的诡辩。你需要特别精确理解的一点是，“P=NP?”只关心是否“能够找到多项式时间算法”，而不关心是否“能够找到快速的多项式时间算法”。也就是说这个多项式算法的复杂度，完全可以是像 n^(10^100) 这样的。所以“P=NP?”的目标，也就是证明是否“能够找到多项式时间算法来解决所有的 NP 问题”，其实对于“找到快速的多项式算法，一点用都没有。

这就好像是一个人说：“我是有钱人。” 等到大家对他刮目相看的时候，他又说：“我有一块钱！” 这好像是很基本的逻辑诡辩，却有很多人被它迷糊了。很多人相信了“P=NP?”的重要性，就是因为没有搞清楚这句话里面的逻辑。

所以，“P=NP?”根本就不需要答案，因为它是一个错误的问题。