逻辑回归

逻辑回归

逻辑回归（Logistic Regression,LR）是一种很常用的分类算法，对于一般的二分类情况，给定N个训练样本，(x1,y1)，(x2,y2)...(xN,yN)，其中xi∈Rn是一个n维向量，yi∈{−1,+1}表示了其对应样本的标签，1代表正样本，-1代表负样本。一般的，逻辑回归模型就是使用sigmoid函数σ(x)=11+exp(−x)将样本特征向量与其属于正样本的概率联系起来：

p(yi=+1|xi,w)=σ(wTxi)=11+exp(−wTxi)同理，样本属于负样本的概率为：

p(yi=−1|xi,w)=1−p(yi=+1|xi,w)=1−11+exp(−wTxi)=exp(−wTxi)1+exp(−wTxi)=11+exp(wTxi)=σ(−wTxi)所以，可以将上述两个式子综合在一起可以得到：

p(yi=±1|xi,w)=σ(yiwTxi)=11+exp(−yiwTxi)有了上述公式，LR的主要目标就是找到一个合适的w，使得上述函数可以将正负样本尽可能的分开。这里寻找w的基本原则是采取统计学中的极大似然估计（Maximun Likelihood Estimation，MLE）。极大似然的中心思想是通过已知的样本，来估计总体的参数。这种思想实际上是一种所谓的“经验风险最小化原则”，相对于经验风险最小化，还有结构风险最小化，后文会对结构风险最小化做进一步解释。

使用极大似然估计求取w的具体方法可以看成如下的一个无约束问题：

maxw∑i=1Nlog(p(yi=±1|xi,w))=maxw−∑i=1Nlog(1+exp(−yiwTxi))消去负号，可将上述最大化问题变为优化问题中常用的最小化问题：

minwl(w)=∑i=1Nlog(1+exp(−yiwTxi))求解上述最优化问题，一般的方法有梯度下降法、牛顿法以及各种改进的拟牛顿法（DFP，BFGS，L-BFGS）具体求解过程这里不做赘述。

结构风险最小化与正则项

当我们数据量较少而特征的属性个数又相对较多时，通过上述方法求得模型可能会出现过拟合，如下图所示：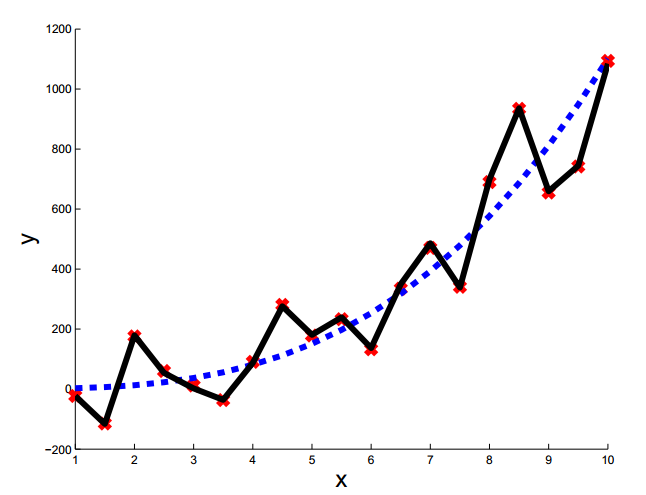


上图中黑色的线是明显出现过拟合的分类线，这种分类器虽然在训练集上有很好的效果（训练误差为0），但是很明显其泛化能力相当差，我们希望得到的是类似于蓝色的分类器。

为了避免出现过拟合的情况，一般加入对模型复杂度的限定，即正则项（Regularizer）。一般常用的正则项有L1和L2正则项。加入正则项后，上述优化问题便成了如下形式：

L1正则项：

minwlog(1+exp(−yiwTxi))+λ||w||L2正则项：

minwlog(1+exp(−yiwTxi))+λ2||w||2上述的带正则项的优化过程就是以结构风险最小化为原则，在寻求经验风险最小的同时还要结合当前模型的复杂度，复杂度越高，惩罚程度也就越大。

逻辑回归用于多分类

逻辑回归用于多分类的思想于二分类的思想很类似，只不过分类函数变了。对于二分类问题来说，其使用的分类函数是sigmoid函数，而多分类则使用softmax函数：

p(y=k|x,w,b)=softmax(wx+b)=exp(wkx+bk)∑iexp(wix+bi)通过上式可以看出，其实二分类问题的sigmoid函数就是softmax的一个特例。对于二分类问题，当p(yi=±1|xi,w)>=0.5时，则认为当前的样本为正样本，p(yi=±1|xi,w)<0.5,则认为当前的样本为负样本。

同理，其损失函数为：

l(w,b)=∑k=1Nlog(p(y=k|x,w,b))