线性回归
2016-06-04 21:29
302 查看
(本文内容来自Andrew NG公开课,首先介绍线性回归模型及求解方法,最后展示实际例子说明问题)
线性回归是监督学习中的一种,数学表述为:数据集中有若干训练数据,对于每个输入特征x(i),有对应输出变量y(i)。我们期望学习一种映射表达y=h(x),使得对于训练集之外的特征也能够较好地预测其输出值。
如果预测值为连续值,这种问题被称为回归问题;而预测值为离散值,则这种问题被称为分类问题。
我们来列举一个简单的回归案例,假设数据特征有两个维度,x={living area,bedrooms},对应房价为输出数据,如下图所示。我们希望建立模型h(x),当给定其他(Living area, bedrooms)数据时,可以预测出对应房型应该支付的房价数额。

1.1 线性回归
线性回归是指使用线性模型对数据进行预测。如果特征x有n个特征维度,xi 表示特征x 的第i 个特征分量。则线性回归模型hθ(x) 为
hθ(x)=∑i=0nθixi=θ0x0=θ1x1+⋯+θnxn=θTx
其中,x0=1。考虑,如果我们知道了预测方程hθ(x), 那么对于任意一个特征,我们就可以根据已知的线性模型推测输出值了。那么这样,问题就转变为如何求线性模型h(x),也就是如何求解h(x)的参数θ 。
考虑采用最小二乘方法,即使得预测值和真实值之间的误差和最小,即,
J(θ)=12∑i=1m(hθ(x(i))−y(i))2
其中,训练集个数为m个,x(i)表示第i个训练数据。
我们期望求解的参数θ 能够使cost function J(θ)最小。这里介绍两种方法求解该问题:Gradient Descent和Normal Equation。
1.2 Gradient Descent
梯度下降法求解回归方程的参数使得cost function最小的基本思路是:赋予初始θ 值,并根据下面公式逐步更新θ 使得J(θ) 不断减少,最终至收敛,对应的参数θ 即为解。θ 的每个分量更新公式为,
θj←θj−α∂∂θjJ(θ)
在更新参数θ 的过程中,我们其实是每次沿着梯度下降的方向按照α 速度下降,直至达到整个函数的局部(全局)最优点,下图就很好的展示了这个过程。
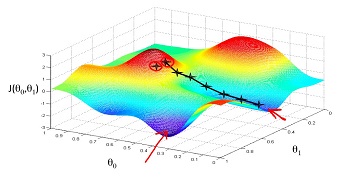
接下来介绍参数更新公式的推导,为了推导方便,首先研究只有一个训练样本时,如何计算推导公式。
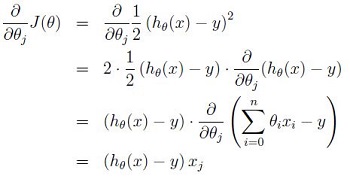
所以,对于单一训练数据而言,模型参数梯度下降的更新公式为,
θj←θj+α(y−hθ(x))xj,j=0,⋯,n
推广至m个训练数据,参数更新公式为,
Repeat until convergence{ θj←θj+α1m∑mi=1(y(i)−hθ(x(i)))x(i)j for every j}
1.2 Normal Equation
Normal Equation是直接使用矩阵X 表示特征数据,y⃗ 表示输出数据,θ表示线性方程参数矩阵。将cost function转换为矩阵表达,通过对参数θ 求导为零,得到的θ 即为使得cost function 最小的线性方程参数。
矩阵表达及参数推导公式如下,
X=⎡⎣⎢⎢⎢⎢⎢⋯⋯⋯(x(1))T(x(2))T⋯(x(m))T⋯⋯⋯⎤⎦⎥⎥⎥⎥⎥y⃗ =⎡⎣⎢⎢⎢⎢y(1)y(2)⋯y(m)⎤⎦⎥⎥⎥⎥θ=⎡⎣⎢⎢⎢⎢θ(1)θ(2)⋯θ(m)⎤⎦⎥⎥⎥⎥
特征数据每一条数据占一行,每一列表示一个特征维度。cost function 表达为,
J(θ)=12∑i=1m(hθ(x(i))−y(i))2=12∑i=1m((x(i))Tθ−y(i))2=12(Xθ−y⃗ )T(Xθ−y⃗ )
cost function相对于参数θ求导公式为(推导公式中引用部分矩阵公式,具体参见Andrew NG课件,此处省略)
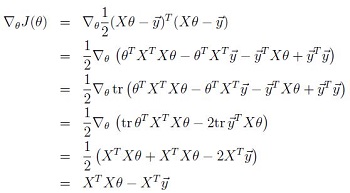
导数为0,可以得到normal equation公式为,
XTXθ=XTy⃗
因此,参数θ 的矩阵表达为,
θ=(XTX)−1XTy⃗
1.3 Gradient Descent和Normal Equation的比较
1.当特征向量不同维度的范围差异较大时,会导致椭圆变得很窄很长,而出现梯度下降困难的问题。而使用Normal Equation是可以不管特征的scale的。(参考1.4部分)
2.相比于Gradient Descent, Normal Equation需要大量的矩阵运算,尤其是矩阵的逆运算,在矩阵很大的情况下,会大大增加计算复杂性。Andrew Ng建议特征维度小于10,000时用Normal Equation,大于10,000时改用Gradient Descent方法。
3.Normal Equation存在不可逆的情况,如:特征向量维度大于特征数量时(n≥m)或者当特征向量不同维度之间存在冗余信息。
1.4 特征缩放(feature scaling)
当特征不同维度之间数值取值范围差异性较大时,梯度下降过程会变得非常缓慢。例如x有两个特征维度,分别表示房屋的面积,取值范围为0-2000,以及房间个数,取值范围为1-5。这两个维度特征的取值规模不在同一个范围内,使用梯度下降时,收敛不快,且容易发生波动。所以在使用梯度下降前,需要将不同维度的特征约束至大致范围内。如,
1.5线性回归案例
案例:特征数据X表示小男孩的年龄,范围在2-8岁之间,输出变量y⃗ 为每个小男孩的高度,共50个样本。求线性回归模型h(x)。
Matlab源代码为
结果展示
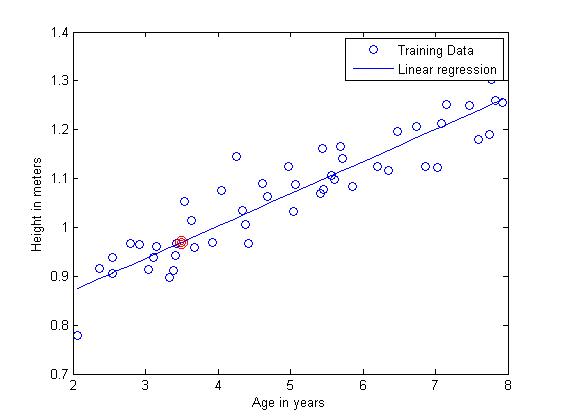
最终求得的参数θ=[0.73900.0659]T。接下来,对新数据age = 3.5进行预测,带入已求得的线性模型,可知高度y = 0.9697,在图中的位置为红色圈表示。
使用Normal Equation计算较为简单,这里不再赘述。
请参考链接:http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex2/ex2.html
线性回归是监督学习中的一种,数学表述为:数据集中有若干训练数据,对于每个输入特征x(i),有对应输出变量y(i)。我们期望学习一种映射表达y=h(x),使得对于训练集之外的特征也能够较好地预测其输出值。
如果预测值为连续值,这种问题被称为回归问题;而预测值为离散值,则这种问题被称为分类问题。
我们来列举一个简单的回归案例,假设数据特征有两个维度,x={living area,bedrooms},对应房价为输出数据,如下图所示。我们希望建立模型h(x),当给定其他(Living area, bedrooms)数据时,可以预测出对应房型应该支付的房价数额。

1.1 线性回归
线性回归是指使用线性模型对数据进行预测。如果特征x有n个特征维度,xi 表示特征x 的第i 个特征分量。则线性回归模型hθ(x) 为
hθ(x)=∑i=0nθixi=θ0x0=θ1x1+⋯+θnxn=θTx
其中,x0=1。考虑,如果我们知道了预测方程hθ(x), 那么对于任意一个特征,我们就可以根据已知的线性模型推测输出值了。那么这样,问题就转变为如何求线性模型h(x),也就是如何求解h(x)的参数θ 。
考虑采用最小二乘方法,即使得预测值和真实值之间的误差和最小,即,
J(θ)=12∑i=1m(hθ(x(i))−y(i))2
其中,训练集个数为m个,x(i)表示第i个训练数据。
我们期望求解的参数θ 能够使cost function J(θ)最小。这里介绍两种方法求解该问题:Gradient Descent和Normal Equation。
1.2 Gradient Descent
梯度下降法求解回归方程的参数使得cost function最小的基本思路是:赋予初始θ 值,并根据下面公式逐步更新θ 使得J(θ) 不断减少,最终至收敛,对应的参数θ 即为解。θ 的每个分量更新公式为,
θj←θj−α∂∂θjJ(θ)
在更新参数θ 的过程中,我们其实是每次沿着梯度下降的方向按照α 速度下降,直至达到整个函数的局部(全局)最优点,下图就很好的展示了这个过程。

接下来介绍参数更新公式的推导,为了推导方便,首先研究只有一个训练样本时,如何计算推导公式。
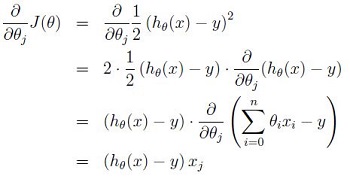
所以,对于单一训练数据而言,模型参数梯度下降的更新公式为,
θj←θj+α(y−hθ(x))xj,j=0,⋯,n
推广至m个训练数据,参数更新公式为,
Repeat until convergence{ θj←θj+α1m∑mi=1(y(i)−hθ(x(i)))x(i)j for every j}
1.2 Normal Equation
Normal Equation是直接使用矩阵X 表示特征数据,y⃗ 表示输出数据,θ表示线性方程参数矩阵。将cost function转换为矩阵表达,通过对参数θ 求导为零,得到的θ 即为使得cost function 最小的线性方程参数。
矩阵表达及参数推导公式如下,
X=⎡⎣⎢⎢⎢⎢⎢⋯⋯⋯(x(1))T(x(2))T⋯(x(m))T⋯⋯⋯⎤⎦⎥⎥⎥⎥⎥y⃗ =⎡⎣⎢⎢⎢⎢y(1)y(2)⋯y(m)⎤⎦⎥⎥⎥⎥θ=⎡⎣⎢⎢⎢⎢θ(1)θ(2)⋯θ(m)⎤⎦⎥⎥⎥⎥
特征数据每一条数据占一行,每一列表示一个特征维度。cost function 表达为,
J(θ)=12∑i=1m(hθ(x(i))−y(i))2=12∑i=1m((x(i))Tθ−y(i))2=12(Xθ−y⃗ )T(Xθ−y⃗ )
cost function相对于参数θ求导公式为(推导公式中引用部分矩阵公式,具体参见Andrew NG课件,此处省略)
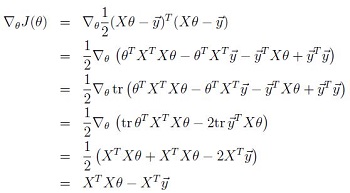
导数为0,可以得到normal equation公式为,
XTXθ=XTy⃗
因此,参数θ 的矩阵表达为,
θ=(XTX)−1XTy⃗
1.3 Gradient Descent和Normal Equation的比较
1.当特征向量不同维度的范围差异较大时,会导致椭圆变得很窄很长,而出现梯度下降困难的问题。而使用Normal Equation是可以不管特征的scale的。(参考1.4部分)
2.相比于Gradient Descent, Normal Equation需要大量的矩阵运算,尤其是矩阵的逆运算,在矩阵很大的情况下,会大大增加计算复杂性。Andrew Ng建议特征维度小于10,000时用Normal Equation,大于10,000时改用Gradient Descent方法。
3.Normal Equation存在不可逆的情况,如:特征向量维度大于特征数量时(n≥m)或者当特征向量不同维度之间存在冗余信息。
1.4 特征缩放(feature scaling)
当特征不同维度之间数值取值范围差异性较大时,梯度下降过程会变得非常缓慢。例如x有两个特征维度,分别表示房屋的面积,取值范围为0-2000,以及房间个数,取值范围为1-5。这两个维度特征的取值规模不在同一个范围内,使用梯度下降时,收敛不快,且容易发生波动。所以在使用梯度下降前,需要将不同维度的特征约束至大致范围内。如,
load('ex3x.dat');
load('ex3y.dat');
m = size(ex3x, 1);
n = size(ex3x, 2) + 1;
x = [ones(m, 1) ex3x];
y = ex3y;
% scaling
mu = mean(x, 1);//均值
sigma = std(x, 1);//方差
for j = 2:n
x(:,j) = (x(:,j) - mu(j))./sigma(j);
end1.5线性回归案例
案例:特征数据X表示小男孩的年龄,范围在2-8岁之间,输出变量y⃗ 为每个小男孩的高度,共50个样本。求线性回归模型h(x)。
Matlab源代码为
%载入数据
x = load('ex2x.dat');
y = load('ex2y.dat');
%绘制数据
figure;
plot(x, y, 'o');
ylabel('Height in meters')
xlabel('Age in years');
%add x0=1
m = size(x, 1);
n = size(x, 2) + 1;
x = [ones(m, 1) x];
alpha = 0.07;
max_iter = 1500;
%iteratively train linear model parameters theta_0 and theta_1
theta = zeros(n, 1);
%first iteration
h = x*theta;
cost_function_pre = sum((h - y).*(h - y),1)/(2);
for j = 1:n
dif = y - h;
theta(j, 1) = theta(j, 1) + alpha * sum(dif.* x(:, j), 1)/m;
end
% second iteration
h = x*theta;
cost_function = sum((h - y).*(h - y),1)/(2);
thred = 0.00001;
iters = 2;
while(abs(cost_function - cost_function_pre) >= thred && iters < max_iter)
iters = iters + 1;
fprintf([num2str(iters) '; cost function:' num2str(iters) '\n']);
% compute theta according to Gradient Descent
for j = 1:n
dif = y - h;
theta(j, 1) = theta(j, 1) + alpha * sum(dif.* x(:, j), 1)/m;
end
cost_function_pre = cost_function;
% compute cost function
h = x*theta;
cost_function = sum((h - y).*(h - y),1)/(2);
end
hold on;
plot(x(:,2), x*theta,'-');
legend('Training Data','Linear regression');结果展示

最终求得的参数θ=[0.73900.0659]T。接下来,对新数据age = 3.5进行预测,带入已求得的线性模型,可知高度y = 0.9697,在图中的位置为红色圈表示。
使用Normal Equation计算较为简单,这里不再赘述。
请参考链接:http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex2/ex2.html
相关文章推荐
- 用Python从零实现贝叶斯分类器的机器学习的教程
- Python编程实现使用线性回归预测数据
- My Machine Learning
- 机器学习---学习首页 3ff0
- Spark机器学习(一) -- Machine Learning Library (MLlib)
- 反向传播(Backpropagation)算法的数学原理
- 关于SVM的那点破事
- 也谈 机器学习到底有没有用 ?
- TensorFlow人工智能引擎入门教程之九 RNN/LSTM循环神经网络长短期记忆网络使用
- TensorFlow人工智能引擎入门教程之十 最强网络 RSNN深度残差网络 平均准确率96-99%
- TensorFlow人工智能引擎入门教程所有目录
- 如何用70行代码实现深度神经网络算法
- 量子计算机编程原理简介 和 机器学习
- 近200篇机器学习&深度学习资料分享(含各种文档,视频,源码等)
- 已经证实提高机器学习模型准确率的八大方法
- 初识机器学习算法有哪些?
- 机器学习相关的库和工具
- 10个关于人工智能和机器学习的有趣开源项目
- 机器学习实践中应避免的7种常见错误
- 机器学习常见的算法面试题总结
