PRML第八章：概率图模型

0 概率&概率图模型

世界的真实状态几乎无法通过我们有限的观测完全确定下来，因为大多数关系根本就是非确定性的，至少相对于我们对其的建模能力而言。不确定性的出现源于我们对世界的观察能力有限，对其建模的能力有限，甚至可能源于其固有的不确定性。由于这种关于真实世界状态的普遍且根本的不确定性的存在，需要我们的推理系统考虑不同的可能性。为了得到有意义的结论，我们不仅需要推理什么是可能的（possible），而且需要推理什么是很可能的（probable）[1]

概率论运算为我们考虑多个可能的结果及其可能性提供了一种形式框架。它定义了一组互斥且无穷尽的可能时间，并赋予每种可能事件一个概率。概率论可以用两个简单的方程表示（加和规则和乘积规则）。PRML第一章

对于高维空间，使用简单的结构化概率模型表示起来会十分复杂。图模型是用图的方式表示概率推理 ，将概率模型可视化，方便展示变量之间的关系。概率图模型能利用复杂分布中的结构来紧凑表示它。



在概率图模型中， 每个节点表示一个随机变量（或一组随机变量），边表示这些变量之间的概率关系。概率图分为有向图和无向图。有向图主要是贝叶斯网络，无向图主要是马尔科夫随机场。

1 贝叶斯网络

1.1 链式法则与贝叶斯公式

条件概率链式法则：

P(A1A2...An)=P(A1)P(A2|A1)...P(An−1|A1A2,,,An−2)P(An|A1A2...An−1)

贝叶斯公式：

P(A|B)=P(B|A)P(A)P(B)

1.2 简单的图模型表示

为了理解有向图对于描述概率分布的作⽤，⾸先考虑三个变量a; b; c上的⼀个任意的联合分布p(a; b; c)。注意，现阶段我们不需要对这些变量做出任何更多的假设，例如它们是离散的还是连续的。实际上，图模型的⼀个强⼤的⽅⾯是，⼀个具体的图可以描述⼀⼤类概率分布。通过使⽤概率的乘积规则，我们可以将联合概率分布写成下⾯的形式。

p(a,b,c)=p(c|a,b)p(a,b)=p(c|a,b)p(b|a)p(a)

关于上式，很有趣的⼀点是，它的左侧关于三个变量a; b; c是对称的，⽽右侧不是。

实际上，通过对左边的分解，我们隐式地选择了⼀个特定的顺序（即a; b; c）。如果选择⼀个不同的顺序，我们会得到⼀个不同的分解⽅式，因此就得到⼀个不同的图表⽰形式。

注意，这个分解⽅法对于任意的联合概率分布的选择都成立。现在，我们使⽤⼀个简单的图模型表示方程的右侧：



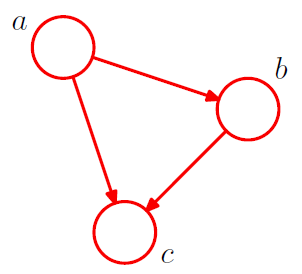
N个变量的联合概率分布

根据1.1中的条件概率链式法则

P(A1A2...An)=P(A1)P(A2|A1)...P(An−1|A1A2,,,An−2)P(An|A1A2...An−1)

我们将1.2中的简单的例子扩展到N个变量的联合概率分布P(A1A2...An)

对应⼀个给定的N，我们可以将其表⽰为⼀个具有N个结点的有向图，每个结点对应于上式右侧的⼀个条件概率分布，每个结点的输⼊链接包括所有以编号低于当前结点编号的结点为起点的链接。我们说，这个图是全连接的（fully connected），因为每对结点之间都存在⼀个链接。

1.3 缺失连接图

⽬前为⽌，我们操作的对象是⼀个完全⼀般的联合概率分布，从⽽分解⽅式以及对应的全连接图表⽰，可以应⽤于概率分布的任意选择。正如我们将会看到的，真正传递出图表⽰的概率分布的性质的有趣信息的是图中链接的缺失（absence）。考虑下图。这不是⼀个全连接的图，因为从x1到x2或者从x3到x7之间不存在链接。



现在，我们将根据这幅图，写出对应的联合概率表达式。联合概率表达式由⼀系列条件概率的乘积组成，每⼀项对应于图中的⼀个结点。每个这样的条件概率分布只以图中对应结点的⽗结点为条件。例如，x5以x1和x3为条件。于是，7个变量的联合概率分布为

p(x1)p(x2)p(x3)p(x4|x1,x2,x3)p(x5|x2,x3)p(x6|x4)p(x7|x4,x5)

条件概率链式法则和贝叶斯网络链式法则差异，比较这个式子和条件概率链式法则的差异

1.4有向图模型的联合概率分布的分解属性

由上面的论述我们可以知道，给定的有向图和变量上对应的概率分布之间的⼀般关系。在图的所有结点上定义的联合概率分布由每个结点上的条件概率分布的乘积表⽰，每个条件概率分布的条件都是图中结点的⽗结点所对应的变量。因此，对于⼀个有K个结点的图，联合概率为

p(x)=∏Kk=1p(xk|pak)

其中，pak表示xk父节点的集合，x={x1,x2,...xk}

注：我们考虑的有向图要满⾜⼀个重要的限制，即不能存在有向环（directed cycle）。换句话说，在图中不能存在这样的路径：从某个结点开始，沿着链接中箭头的⽅向运动，结束点为起点。这种没有有向环的图被称为有向⽆环图（directed acyclic graph），或者DAG。这等价于存在⼀个将诶点的排序，使得不存在从某个结点到序号较⼩的结点的链接。

1.5 条件独立

2 马尔科夫随机场

3 因子图

From:

Ref:

[1] Probabilistic Graphical Models Principles and Techniques. Daphne Koller,Nir Friedman

[2] Pattern Recognition and Machine Learning. Chapter 8

[3] http://www.cnblogs.com/bhlsheji/p/4875551.html