卡特兰数

卡塔兰数

卡塔兰数是组合数学中一个常出现在各种计数问题中出现的数列。
卡塔兰数的一般项公式为


另类递归式： h(n)=((4*n-2)/(n+1))*h(n-1);
前几项为 （OEIS中的数列A000108）:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786,
208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190,
6564120420,
24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452,...

性质

Cn的另一个表达形式为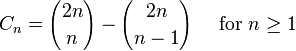

所以，Cn是一个自然数；这一点在先前的
通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)
卡塔兰数满足以下递推关系



它也满足



这提供了一个更快速的方法来计算卡塔兰数。
卡塔兰数的渐近增长为



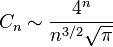
它的含义是左式除以右式的商趋向于1当n → ∞。（这可以用n!的斯特灵公式来证明。）
所有的奇卡塔兰数Cn都满足n = 2k − 1。所有其他的卡塔兰数都是偶数。

卡特兰数的几何证明：

事实上，可以认为问题是，任意两种操作，要求每种操作的总次数一样，且进行第k次操作2前必须先进行至
少k次操作1。我们假设一个人在原点，操作1是此人沿右上角45°走一个单位（一个单位设为根号2，这样他
第一次进行操作1就刚好走到（1,1）点），操作2是此人沿右下角45°走一个单位。第k次操作2前必须先进
行至少k次操作1，就是说明所走出来的折线不能跨越x轴走到y=-1这条线上！在进行n次操作1和n此操作2
后，此人必将到到达（2n，0）！若无跨越x轴的限制，折线的种数将为C（2n，n），即在2n次操作中选出
n次作为操作1的方法数。



现在只要减去跨越了x轴的情况数。对于任意跨越x轴的情况，必有将与y=-1相交。对于每条跨越X轴的折线，

找出第一个与y=-1相交的点k，将k点以右的折线根据直线：y=-1对称（即操作1与操作2互换了）。

可以发现终点最终都会从（2n，0）对称到（2n，-2），且我们保证了折线的连续性，即K点位置是不变。

由于对称总是能进行的，且是可逆的。

我们可以得出所有跨越了x轴的折线总数是与从（0,0）到（2n,-2）的折线总数。

而后者的操作2比操作1要多0-（-2）=2次。即操作1为n-1,操作2为n+1。总数为C（2n，n-1）。