[置顶] 二叉搜索树的搜索、插入、后继、删除
2016-02-17 15:13
323 查看
二叉搜索树
二叉搜索树支持Insert、Delete、Search、Maximum、MInimum、Predecessor(前驱结点)、Successor(后继结点)等操作。二叉搜索树的基本操作与树的高度成正比,对于一个有n个结点的完全二叉树来说,这些操作的最坏运行时间为O(lg n)。若要将n个结点组织成一个线性链,最坏运行时间将达到O(n)。
下面是二叉搜索树的定义:
遍历
查找
从根结点开始进行比较,若给定结点的key大于根结点,则沿右子树继续查找;若小于根结点的key,则沿着左子树查找。直到找到返回该结点为止,否则返回NULL。
上面是递归实现的Search,下面是迭代实现的:<
4000
/p>
除了上述查找操作,还有Maximum和Minimum,即查找以为某一结点为根的子树中的最小结点(仅以Minimum为例)。
前驱和后继
寻找后继结点分两种情况:
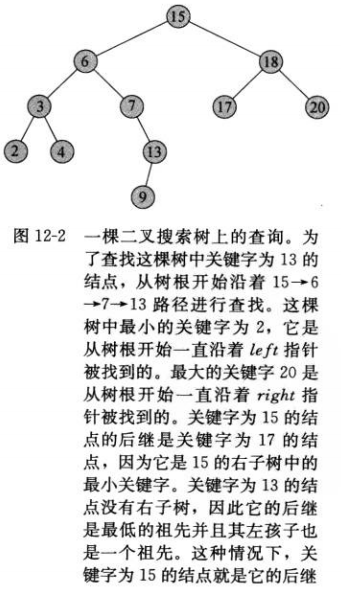
结点x的右子树非空。则x的后继几点恰好是x的右子树中的最左的结点,也就是x右子树中的最小结点。(例如根结点15的后继是17)
结点x的右子树为空,并且x有一个后继y。为了找到y,只要从x开始沿树而上,直到遇到一个其双亲有左孩子的结点。(13的后继为15)
以上是二叉搜索树的几个简单基本操作。Insert操作仅需要按照二叉搜索树的性质将结点插入相应位置即可。
下面是Insert的代码:
最复杂就是删除结点的操作,要用到以上相关操作…………下次再写Delete
————————————————————————————————————
接着昨天未完成的Delete函数
对于删除一棵二叉搜索树的节点x来说,分以下三种情况:
被删除结点为叶子结点。一种可能该结点是根结点,直接删除,并修改指针即可;另一种可能该结点为非根叶子结点,这样直接将其双亲的左(右)孩子置为空。
只有一个孩子结点(左孩子 or 右孩子)。以仅有左孩子为例,将x的左孩子的双亲指向x的双亲结点,将x的双亲的孩子结点指向x的左孩子。
x的左右孩子结点都存在。这种情况下,先找到x的右子树中最小的结点y(y无左子树)。若y的双亲结点是x,那么用y.key替换x.key,再删除y结点街可以了;若y的双亲结点不为x,则让y的双亲的孩子指向y的右孩子,y的右孩子的双亲指向y的双亲,最后用y.key替换x.key,再free掉y即可。
下面是Delete函数:
总结:本来Delete函数思路不是特别复杂,但是在修改指针时还要判断被删结点x是其双亲结点的左孩子还是右孩子,所以在只有一个子树的情况中,代码显得有些冗杂。
二叉搜索树是以二叉树是形式表示的,这样就可以使用一个二叉链表来表示二叉搜索树了。 对于任何结点x,其左子树的关键字的值不大于x.key,右子树的关键字不小于x.key。
二叉搜索树支持Insert、Delete、Search、Maximum、MInimum、Predecessor(前驱结点)、Successor(后继结点)等操作。二叉搜索树的基本操作与树的高度成正比,对于一个有n个结点的完全二叉树来说,这些操作的最坏运行时间为O(lg n)。若要将n个结点组织成一个线性链,最坏运行时间将达到O(n)。
下面是二叉搜索树的定义:
typedef struct Binary_Search_Tree bTree;
struct struct Binary_Search_Tree
{
int key;
bTree *left;
bTree *right;
bTree *parent;//指向父结点
}*pNode;遍历
由于左子树 <= 结点 <= 右子树,所以就可以用中序遍历就可以将一棵二叉搜索树按顺序输出。
Inorder_bTree(pNode *root)
{
if(root != NULL)
{
Inorder_bTree(root->left);
printf("%d ", root->key);
Inorder_bTree(root->right);
}
}查找
从根结点开始进行比较,若给定结点的key大于根结点,则沿右子树继续查找;若小于根结点的key,则沿着左子树查找。直到找到返回该结点为止,否则返回NULL。
bTree Search(pNode *root, int key)
{
if(root == NULL || root->key == key)
return root;
if(key < root->key)
return Search(root->left, key);
else
return Search(root->right, key);
}上面是递归实现的Search,下面是迭代实现的:<
4000
/p>
bTree Search(pNode *root, int key)
{
while(root != NULL && root->key != key)
{
if(key < root->key)
root = root->left;
else
root = root->right;
}
if(root->key == key)
return root;
else
return root;
}除了上述查找操作,还有Maximum和Minimum,即查找以为某一结点为根的子树中的最小结点(仅以Minimum为例)。
bTree Minimum(pNode *root)
{
while(root->left != NULL)
root = root->left;
return root;
}前驱和后继
给定一个结点x,大于x.key的最小关键字结点就是x的后继结点。如果后继存在,就返回x的后继结点;若x的关键字就是这棵树中最大的,就返回NULL。
寻找后继结点分两种情况:
结点x的右子树非空。则x的后继几点恰好是x的右子树中的最左的结点,也就是x右子树中的最小结点。(例如根结点15的后继是17)
结点x的右子树为空,并且x有一个后继y。为了找到y,只要从x开始沿树而上,直到遇到一个其双亲有左孩子的结点。(13的后继为15)

pTree Successor(pNode *root)
{
// if(root == Maximum(root))
// return NULL;
if(root->right != NULL)
return Minimum(root->right);
pNode *y;
y = root->parent;
while(y != NULL && root == y->right)
{
root = y;
y = y->parent;
}
return y;
}以上是二叉搜索树的几个简单基本操作。Insert操作仅需要按照二叉搜索树的性质将结点插入相应位置即可。
下面是Insert的代码:
Insert(pNode *root, bTree t)//t为待插入结点
{
bTree *y, *x;
y = NULL;
x = root;
while(x != NULL)//找到t的双亲结点y
{
y = x;
if(t->key < x->key)
x = x->left;
else
x = x->right;
}
t->parent = y;
if(y == NULL)//待插入二叉树为空
root = t;
else if(t->key < y->key)/*判断待插入结点是作为双亲结点的左子树还是右子树*/
y->left = t;
else
y->right = t;
}最复杂就是删除结点的操作,要用到以上相关操作…………下次再写Delete
————————————————————————————————————
接着昨天未完成的Delete函数
对于删除一棵二叉搜索树的节点x来说,分以下三种情况:
被删除结点为叶子结点。一种可能该结点是根结点,直接删除,并修改指针即可;另一种可能该结点为非根叶子结点,这样直接将其双亲的左(右)孩子置为空。
只有一个孩子结点(左孩子 or 右孩子)。以仅有左孩子为例,将x的左孩子的双亲指向x的双亲结点,将x的双亲的孩子结点指向x的左孩子。
x的左右孩子结点都存在。这种情况下,先找到x的右子树中最小的结点y(y无左子树)。若y的双亲结点是x,那么用y.key替换x.key,再删除y结点街可以了;若y的双亲结点不为x,则让y的双亲的孩子指向y的右孩子,y的右孩子的双亲指向y的双亲,最后用y.key替换x.key,再free掉y即可。
下面是Delete函数:
void Delete(pNode *root, bTree x)
{
if(x == NULL)
return;
if(x->left == NULL && x->right == NULL)//x是叶子结点的情况
{
if(x->parent == NULL)//x是根结点
{
free(x);
(*root)=NULL;
}
else //x是非根叶子结点
{
if(x->parent->left == x)
x->parent->left=NULL;
else
x->parent->right=NULL;
free(x);
}
}
else if(x->right != NULL && x->left== NULL)//只有右子树的情况
{
x->right->parent = x->parent;
if(x->parent == NULL)
*root=x->right;
else if(x->parent->left == x)
x->parent->left = x->right;
else
x->parent->right = x->right;
free(x);
}
else if(x->left != NULL && x->right == NULL)//只有左子树的情况
{
x->left->parent = x->parent;
if(x->parent == NULL)
*root=x->left;
else if(x->parent->left == x)
x->parent->left = x->left;
else
x->parent->right = x->left;
free(x);
}
else//左右孩子都存在的情况
{
bTree temp = Minimum(x->right);//找到x的右子树中key最小的结点
if(temp->parent == x)//temp为x的右子树
{
x->right = NULL;
x->right->parent = NULL:
x->key = temp->key;
}
else
{
temp->parent->left = temp->right;
temp->right->parent = temp->parent;
x->key = temp->key
}
free(temp);
}
}总结:本来Delete函数思路不是特别复杂,但是在修改指针时还要判断被删结点x是其双亲结点的左孩子还是右孩子,所以在只有一个子树的情况中,代码显得有些冗杂。
在《算法导论》中,关于二叉搜索树的删除给出了一个Transplant函数作为Delete的内部函数使用,但还是觉得不如自己思路来的清晰。有兴趣的可以查阅该书(第三版)的168页来研究一下。
相关文章推荐
- maven打包加时间戳
- 打开linux主机的端口快速释放
- Xcode报png图片格式错误
- Ubuntu下如何解压缩zip,tar,tar.gz,tar.bz2文件
- 【codevs1021】玛丽卡,以前屯着的最短路
- python 算法基础查找和二维数组转换
- loadScript,非阻塞 JavaScript 加载库
- Tomcat报错—Tomcat内存溢出及大小调整
- 高德地图API KEY出现INVALID_USER_SCODE的解决过程
- 配置gosublime
- 导航属性(外键)
- 解决:本地测试wordpress安装主题需要FTP问题
- Spring MVC和Struts2的比较
- 分治法(divide & conquer algorithm)的理解
- 灵活运用IOS类别(Category)和扩展(Extension)
- unity3d深入学习笔记4:AnySdk接入
- iOS storyboard tableview 内容下移64
- Errore Http 404.2
- iOS plist文件创建
- Spring中MultipartHttpServletRequest实现文件上传
