红黑树
2016-01-25 15:21
232 查看
红黑树
红黑树是一种二叉查找树, 每个节点有一个存储位,表示颜色, red or black, 通过任何一条从根到叶子的路径上的各个节点的着色限制,红黑树确保没有一条路径会比其他路径长2倍,因而是接近平衡的。
1.红黑树性质
1> 每个节点要么是红色的要么是黑色的。
2> 根节点是黑色的。
3>每个叶子节点(nil) 是黑色的
4>如果一个节点是红色的,则它的儿子节点一定都是黑色的
5>对于每个节点,对于从该节点到其子孙节点的各个路径上黑色节点的数目是一致的。

这里我们把所有 null 归纳成一个哨兵节点nil[T],并且根节点的父亲也是这个哨兵节点,这样写代码的时候比较方便。
首先一个有n个内节点的红黑树的高度之多为2lg(n+1);
证明:
首先我们将从某个节点x出发到一个也节点的任意一条路径上的黑色节点的个数称为该节点的黑高度 hb(x);
我们首先来证明 一个根节点为x的红黑树至少有 2^(hb(x)) - 1个内节点。
证明如下:
首先当 x = 0 时, 2^0 - 1 = 0, 没有问题
当x > 0 时, 假设x的黑高度为 hb(x), 那么其儿女节点的黑高度为 hb(x) or hb(x) - 1,利用归纳假设,可以得到每个节点至少 2^(hb(x)) - 1个内节点。
那么也就是说 n >= 2^(hb(x)) - 1
那么根据红黑树的性质4>, hb(x) >= h/2
所以 n >= 2^(h/2) - 1
那么就有 h <= 2lg(n + 1);
所以 红黑树的 时间复杂度时O(lgn);
2.旋转操作
由于插入新的节点, 以及删除及诶单可能会改变红黑树的性质,所以必须要通过旋转和改变颜色状态来确保插入后的树,仍是一棵红黑树,旋转的左旋右旋操作根AVL-Tree。
3插入操作
像一棵红黑树里插入一个节点的时间复杂度是可以在 O(lgn) 内完成的.为了确保 性质5的成立,我们插入的节点一定是红色的。
我们先来看下伪代码(参考算法导论)
由于我们添加了红色节点,所以可能违反了 2> , 4> 所以需要 RB-INSERT-FIXUP(T, z)
插入的时候分以下几种情况:
1> 当叔父节点是红色的时候, 那么直接改变 以下几个节点的颜色: color[p[z]] = color[uncle[z]] = red color[z] = black 此时违反情况的可能是 p[z] 所以再 另 z = p[z] 然后再继续循环
2> 当叔父节点是黑色的时候, 这时候分四种情况:
case 1 :

图中的N就相当于伪代码里的z, 当 p[z] == left[p[p[z]]] 时, 我们可以 : color[p[z]] = black, color[p[p[z]]] = red, ( p[z] = P , p[p[z]] = G) 那这样会造成右半枝黑色少一个, 那么对 p[p[z]] (G)进行右旋, 这样又“平衡了”
case 2:
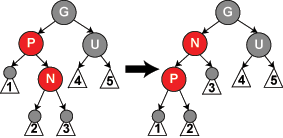
当图中N是 P 的右孩子时, 那么只要进行一个左旋又会变成 case 1 的形势,
case 3 , case 4 其实原理同上,只不过就是旋转的时候要注意下,根前面不太一样
删除:
我们再删除的时候,是找其后继节点进行替换,实际删除的节点时其后继节点, 只不过把我们期望删除节点的值改成其后继及节点,那么我们在删除的时候就会产生一些问题,如果删除的节点是红色的节点,那么对原路径没什么影响,但是如果删除的y是黑色的节点,那么就有可能违反 性质 1>, 2> ,4>
其实我们可以把x节点看作是一个双重的黑色节点活着一个红黑色及诶单,也就是保证性质 5> 的成立,( x 是y 的 子节点),当删除黑节点y时,将其黑色下推至其子节点。那么现在问题变成节点x既不是红色也不是黑色,违反了性质 1>,节点x时双重色,这就分别给有x存在的路径上的黑高度贡献1 或者 2
其实上面的伪代码主要是将多余的黑色向上移动,直到:
1> x 指向一个红黑色极点, 此时将 color[x] 改为 black
2> x指向root 这是可以简单的消除那个额外的黑色
3> 做必要的旋转和颜色修改
N表示要删除的节点
我们只讨论左半枝的情况,右半枝只不过是左右 调换一下
case 1:如果其兄弟节点时红色的那么其 父亲节点一定时黑色的

如果其兄弟节点时红色的那么其 父亲节点一定时黑色的。因为 S是红色的那么根据性质,其必有黑色的孩子节点,我们可以改变 S 和 P的颜色, 再会P做一次左旋, 这样红黑树的性质得以保持,这样情况就转换成剩余的情况了,并且 N 的新兄弟是旋转前S的孩子。
case: 2 当 x的兄弟是黑色,并且其兄的的两个孩子都是黑色的时候。P 的颜色是黑色(x 就是图中的N)

这样的话 N 可以从 S 身上去掉一层黑色, 但是这个时候并没有结束,为了补偿从N 和 S上少的一个黑色,我们想从P上增加额外的 一个黑色, 可以通过 让 x 指针指向 P(即 x <- p[x]) 来重新循环
case 3 当 x 的兄弟是黑色, 并且其兄的的两个孩子时时黑色。并且 P 时红色

这种情况比较简单,我们只要从 S 上去掉 N 多的一重黑色, 再从P上补充N 和 S 都 少的一重黑色就ok
case 4 当 x 的兄弟时黑色, 其兄弟的左孩子红色, 右孩子黑色
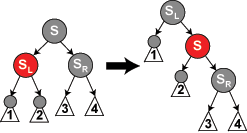
这样我们对S 进行右旋, 那么就是进入了下一种情况并且,原来的红黑树性质不变
case 5 当其 兄弟是黑色, 右孩子时红色, 左孩子时黑色
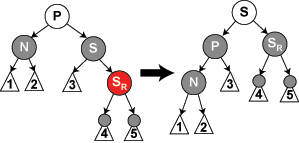
其实我们就是想给 N 这枝加上一个黑色,那么我们直接可以把SR改为黑色,把 P 和 S的颜色交换,再做一个左旋
红黑树是一种二叉查找树, 每个节点有一个存储位,表示颜色, red or black, 通过任何一条从根到叶子的路径上的各个节点的着色限制,红黑树确保没有一条路径会比其他路径长2倍,因而是接近平衡的。
1.红黑树性质
1> 每个节点要么是红色的要么是黑色的。
2> 根节点是黑色的。
3>每个叶子节点(nil) 是黑色的
4>如果一个节点是红色的,则它的儿子节点一定都是黑色的
5>对于每个节点,对于从该节点到其子孙节点的各个路径上黑色节点的数目是一致的。

这里我们把所有 null 归纳成一个哨兵节点nil[T],并且根节点的父亲也是这个哨兵节点,这样写代码的时候比较方便。
首先一个有n个内节点的红黑树的高度之多为2lg(n+1);
证明:
首先我们将从某个节点x出发到一个也节点的任意一条路径上的黑色节点的个数称为该节点的黑高度 hb(x);
我们首先来证明 一个根节点为x的红黑树至少有 2^(hb(x)) - 1个内节点。
证明如下:
首先当 x = 0 时, 2^0 - 1 = 0, 没有问题
当x > 0 时, 假设x的黑高度为 hb(x), 那么其儿女节点的黑高度为 hb(x) or hb(x) - 1,利用归纳假设,可以得到每个节点至少 2^(hb(x)) - 1个内节点。
那么也就是说 n >= 2^(hb(x)) - 1
那么根据红黑树的性质4>, hb(x) >= h/2
所以 n >= 2^(h/2) - 1
那么就有 h <= 2lg(n + 1);
所以 红黑树的 时间复杂度时O(lgn);
2.旋转操作
由于插入新的节点, 以及删除及诶单可能会改变红黑树的性质,所以必须要通过旋转和改变颜色状态来确保插入后的树,仍是一棵红黑树,旋转的左旋右旋操作根AVL-Tree。
3插入操作
像一棵红黑树里插入一个节点的时间复杂度是可以在 O(lgn) 内完成的.为了确保 性质5的成立,我们插入的节点一定是红色的。
我们先来看下伪代码(参考算法导论)
RB-INSERT(T, z) y<-nil[T]; x<-root[T]; while x != nil[T] do y <- x if key[z] > key[x] then x <- right[x] else x <- left[x] p[z]<-y; if y == nil[T] then root[T] <- z else if key[y] > key[z] left[y] <- z else right[y] <- z left[z] <- nil[T] right[z] <- nil[T] color[z] <- RED RB-INSERT-FIXUP(T, z);
由于我们添加了红色节点,所以可能违反了 2> , 4> 所以需要 RB-INSERT-FIXUP(T, z)
RB-INSERT-FIXUP(T ,z) while(color[p[z]] == RED) do if p[z] == left[p[p[z]]] then y <- right[p[p[z]]] if color[y] == RED then color[p[z]] <- black color[y] <- black color[p[y]] <- red z<- p[y] else if z == right[p[z]] then z<-p[z] LEFT-ROTATE(T, z) color[p[z]] <- balck color[p[p[z]]] <- red RIGHT-ROTATE(T, p[p[z]]) else if p[z] == right[p[p[z]]] then y <- left[p[p[z]]] if color[y] == red then color[p[z]] <- black color[y]<-black color[p[y]] <- red z = p[y] else if color[y] == black if z == left[p[z]] then z = p[z] RIGHT-ROTATE(T, z) color[p[p[z]]] = red color[p[z]] = back LEFT-ROTATE(T, p[p[z]]) color[root[T]]= balck
插入的时候分以下几种情况:
1> 当叔父节点是红色的时候, 那么直接改变 以下几个节点的颜色: color[p[z]] = color[uncle[z]] = red color[z] = black 此时违反情况的可能是 p[z] 所以再 另 z = p[z] 然后再继续循环
2> 当叔父节点是黑色的时候, 这时候分四种情况:
case 1 :

图中的N就相当于伪代码里的z, 当 p[z] == left[p[p[z]]] 时, 我们可以 : color[p[z]] = black, color[p[p[z]]] = red, ( p[z] = P , p[p[z]] = G) 那这样会造成右半枝黑色少一个, 那么对 p[p[z]] (G)进行右旋, 这样又“平衡了”
case 2:

当图中N是 P 的右孩子时, 那么只要进行一个左旋又会变成 case 1 的形势,
case 3 , case 4 其实原理同上,只不过就是旋转的时候要注意下,根前面不太一样
删除:
RB-DELETE(T, z) if left[z] = nil[T] and right[z] = nil[T] then y<-z else y<-TREE-SUCCESSOR(z) if left[y] != nil[T] then x <- left[y] else x<-right[y] p[x] = p[y] if p[y] = nil[T] then root[T] <- x else if y = left[p[y]] then left[p[y]] <- x else right[p[y]] <- x if y != z then key[z] <- key[y] if color[y] == black then RB-DELETE-FIXUP(T, x) return y TREE-SUCCESSOR(x) if right[x] != NIL then return TREE-MINMUM(right[x]) y<-p[x] while y != NIL and x == right[y] do x <- y y <- p[y] return y RT-DELETE-FIXUP(x) while x != root[T] and color[x] = black do if x = left[p[x]] then w <- right[p[x]] if color[w] = red then color[w] <- black color[p[x]] <- red left-rotate(T, p[x]) w <- right[p[x]] if color[left[w]] = black and color[right[w]] = black then color[w] <- red x <- p[x] else if color[right[w]] = black then color[left[w]] <- black color[w] <- red RIGHT-ROTATE(T, p[x]) x <- root[T] else
我们再删除的时候,是找其后继节点进行替换,实际删除的节点时其后继节点, 只不过把我们期望删除节点的值改成其后继及节点,那么我们在删除的时候就会产生一些问题,如果删除的节点是红色的节点,那么对原路径没什么影响,但是如果删除的y是黑色的节点,那么就有可能违反 性质 1>, 2> ,4>
其实我们可以把x节点看作是一个双重的黑色节点活着一个红黑色及诶单,也就是保证性质 5> 的成立,( x 是y 的 子节点),当删除黑节点y时,将其黑色下推至其子节点。那么现在问题变成节点x既不是红色也不是黑色,违反了性质 1>,节点x时双重色,这就分别给有x存在的路径上的黑高度贡献1 或者 2
其实上面的伪代码主要是将多余的黑色向上移动,直到:
1> x 指向一个红黑色极点, 此时将 color[x] 改为 black
2> x指向root 这是可以简单的消除那个额外的黑色
3> 做必要的旋转和颜色修改
N表示要删除的节点
我们只讨论左半枝的情况,右半枝只不过是左右 调换一下
case 1:如果其兄弟节点时红色的那么其 父亲节点一定时黑色的

如果其兄弟节点时红色的那么其 父亲节点一定时黑色的。因为 S是红色的那么根据性质,其必有黑色的孩子节点,我们可以改变 S 和 P的颜色, 再会P做一次左旋, 这样红黑树的性质得以保持,这样情况就转换成剩余的情况了,并且 N 的新兄弟是旋转前S的孩子。
case: 2 当 x的兄弟是黑色,并且其兄的的两个孩子都是黑色的时候。P 的颜色是黑色(x 就是图中的N)

这样的话 N 可以从 S 身上去掉一层黑色, 但是这个时候并没有结束,为了补偿从N 和 S上少的一个黑色,我们想从P上增加额外的 一个黑色, 可以通过 让 x 指针指向 P(即 x <- p[x]) 来重新循环
case 3 当 x 的兄弟是黑色, 并且其兄的的两个孩子时时黑色。并且 P 时红色

这种情况比较简单,我们只要从 S 上去掉 N 多的一重黑色, 再从P上补充N 和 S 都 少的一重黑色就ok
case 4 当 x 的兄弟时黑色, 其兄弟的左孩子红色, 右孩子黑色

这样我们对S 进行右旋, 那么就是进入了下一种情况并且,原来的红黑树性质不变
case 5 当其 兄弟是黑色, 右孩子时红色, 左孩子时黑色

其实我们就是想给 N 这枝加上一个黑色,那么我们直接可以把SR改为黑色,把 P 和 S的颜色交换,再做一个左旋
相关文章推荐
- js 获取image 的宽高
- Mac OS X 上Android手机连接adb的解决方案。
- Android应用程序在新的进程中启动新的Activity的方法和过程分析
- 图片保存到本地
- tomcat + redis 实现session共享
- 虚拟化 知识汇总
- 移位运算符
- linux (1)基本知识/目录/磁盘格式/文件系统
- 爬虫防掉线
- MyBitis(iBitis)系列随笔之五:多表(一对多关联查询)
- 学生信息管理系统v1.0
- TortoiseSVN中分支和合并实践
- Notepad++配置Python开发环境
- hook模板x86/x64通用版(1)--x64下的jmp远跳、远call指令
- 内部类
- Spfile、Pfile的修改相关
- OTA和Recovery系统升级流程介绍
- 【慕课笔记】U1 类和对象 第1节 什么是类和对象
- OS
- JavaScript:函数
