【算法分析】QQ“一键退朝”之详细计算方法
2015-12-23 15:31
645 查看
相信很多朋友和我一样很喜欢QQ上“一键退朝”的功能,就是把红点从它原本的地方拉走,消息提醒也就没有了。
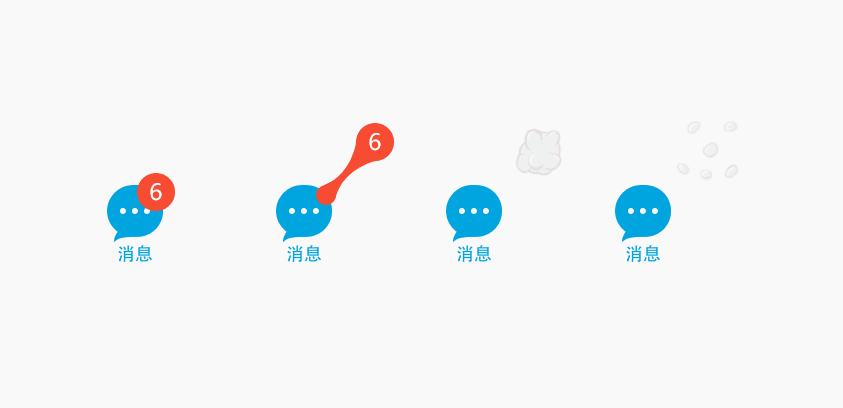
直到如今我还是觉得这个功能很酷炫!于是想自己实现一番,经过一番调查知道拉伸其实就是由两个圆加上两条贝塞尔曲线组成的形状。
来看看腾讯设计师是怎么设计出来的吧:《QQ手机版 5.0“一键下班”设计小结》
看完了这个对实现思路有很大的帮助,可是我还是不能知道具体是怎么计算实现的,网上大部分的教程都是假想成了两个同样大小的圆来计算,这太取巧了!因为同样大小的圆两条外公切线是平行的,同一个圆上的公切点相连是会垂直于连心线的,但是大小不同的圆并没有这个特殊性!
另外网上也有很多仿照的项目,可是看算法看得头都大了也不明白为什么是这样算的!经过两天的研究,把初中数学(圆、三角函数等相关知识)好好复习了一遍,终于搞清楚了其中算法,现在跟我一起来看看吧!
建立两圆的相对坐标系:

PS:在移动端的坐标系 yy 轴是向下的。
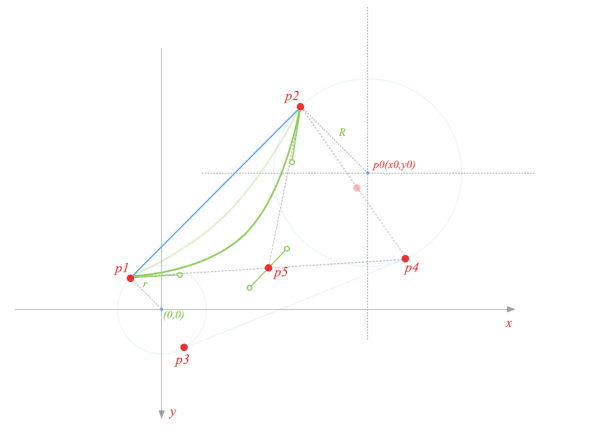
假设某一个时刻,两圆的状态如图,我们现在可以确定的是小圆的圆心坐标 OO 为(startXstartX, startYstartY),大圆的圆心坐标 P0P_{0} 为 (x0x_{0}, y0y_{0}),以及小圆的半径 rr 和大圆的半径 RR 。
那么首先可以把连心线求出来!也就是 OP0OP_{0} 的距离。
连心线的长度:d=(x0−startX)2+(y0−startY)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√连心线的长度:d = \sqrt{ (x_{0} - startX)^{2}+ (y_{0} - startY)^{2}}
两个外离的圆,一定有两条外公切线。若两圆半径相同,则两外公切线平行;否则相交于一点,且该点与两圆心在同一直线。
我们再作一张有公切线的图:

切点为 P1、P2、P3、P4P_{1}、P_{2}、P_{3}、P_{4},我们现在目的就要求出这四个点,然后就能够在程序中画出切线。
整个算法最难的地方恐怕就是求这四个点了,我们需要借助作图来帮助计算,这之前还需要先复习下定理:
圆心和切点的连线一定垂直于过该点的公切线
首先过小圆圆心 OO 作一条平行于 P1P2P_{1}P_{2} 的线,和 P0P2P_{0}P_{2} 相交于点 MM ,可以得到 P1OMP2P_{1}OMP_{2} 为一个矩形,则 P2M=P1O=rP_{2}M = P_{1}O = r ,又因为 P2P0=RP_{2}P_{0} = R ,所以 P0M=R−rP_{0}M = R-r ,那么
可求:sinγ=sin∠MOP0=MP0OP0=R−rd可求:sin\gamma = sin\angle MOP_{0} = \frac{MP_{0}}{OP_{0}} = \frac{R - r}{d}
即:γ=∠MOP0=arcsinR−rd即:\gamma = \angle MOP_{0} = arcsin \frac{R - r}{d}
作连心线和 xx 轴的夹角为 α \alpha
可求:tanα=startY−y0x0−startX可求: tan\alpha = \frac{startY - y_{0}}{x_{0} - startX}
即:∠α=arctanstartY−y0x0−startX即:\angle\alpha = arctan \frac{startY - y_{0}}{x_{0} - startX}
再作几个辅助点 A、B、C、DA、B、C、D,ABAB 表示以大圆圆心为原点的坐标系的 xx 轴的两端,CDCD 表示以小圆圆心为原点的坐标系的 xx 轴的两端,

∵AB//CD,∠P0OD=α∵AB // CD,\angle P_{0}OD = \alpha
∴∠AP0O=α∴\angle AP_{0}O = \alpha
∵∠P1OC=β,P1O//P2P0∵\angle P_{1}OC = \beta ,P_{1}O // P_{2}P_{0}
∴∠P2P0A=∠P1OC=β∴\angle P_{2}P_{0}A =\angle P_{1}OC = \beta
又∵OM⊥P2P0,得出∠OMP0=90°,即弧度值π2又∵OM \perp P_{2}P_{0} ,得出 \angle OMP_{0} = 90° ,即弧度值\frac{\pi}{2}
∴β=π2−γ−α∴\beta = \frac{\pi}{2} - \gamma - \alpha
现在 β\beta 求出来了,两圆的半径也已知,求 P1、P2P_{1}、P_{2} 的坐标是不是很简单?
综上:P1.x=startX−cosβ∗r,P1.y=startY−sinβ∗r综上:P_{1}.x = startX - cos\beta * r,P_{1}.y = startY - sin\beta * r
P2.x=x0−cosβ∗R,P1.y=y0−sinβ∗RP_{2}.x = x_{0}- cos\beta * R,P_{1}.y = y_{0} - sin\beta * R

为了能愉快阅读,再来复习一下各种拉丁希腊符号叫法:
α 阿尔法 β 贝塔 γ 伽玛 δ 德尔塔 ε 伊普西隆 ζ 泽塔
如上图作辅助线。
由于圆的对称性可知:∠P0ON=γ由于圆的对称性可知:\angle P_{0}ON = \gamma
∵δ+α=90°,即弧度值π2∵\delta + \alpha = 90°,即弧度值\frac{\pi}{2}
∴δ=π2−α∴\delta = \frac{\pi}{2} - \alpha
又∵ON⊥P0P4又∵ON \bot P_{0}P_{4}
∴γ+δ+ε=π2,即求出ε=π2−γ−δ∴\gamma +\delta + \varepsilon = \frac{\pi}{2},即求出\varepsilon = \frac{\pi}{2} -\gamma - \delta
又∵ε+ζ=π2又∵ \varepsilon + \zeta = \frac{\pi}{2}
综上,ζ=π2−ε=π2−(π2−γ−δ)=π2−(π2−γ−(π2−α))综上,\zeta = \frac{\pi}{2} - \varepsilon = \frac{\pi}{2} - (\frac{\pi}{2} -\gamma - \delta) = \frac{\pi}{2} - (\frac{\pi}{2} -\gamma - (\frac{\pi}{2} - \alpha))
即求出:ζ=π2+γ−α即求出:\zeta = \frac{\pi}{2} + \gamma - \alpha
在前面 γ\gamma 和 α\alpha 已经求出来了!那么 P4P_{4} 坐标也就不难了。
综上:P3.x=startX+cosζ∗r,P3.y=startY+sinζ∗r综上:P_{3}.x = startX + cos\zeta * r,P_{3}.y = startY + sin\zeta * r
P4.x=x0+cosζ∗R,P4.y=y0+sinζ∗RP_{4}.x = x_{0}+ cos\zeta * R,P_{4}.y = y_{0} + sin\zeta * R
如果我们把画一条直线分为进度100%的话,那么当进度为0%,12%,58%,74%时,画线的状态为(注意红色部分末的黑色端点,灰色部分为路径指示)




那么把所有时刻的黑点连接起来就构成了直线:

这个概念应该比较容易接受,好了继续。
二次贝塞尔曲线(最简单的贝塞尔曲线)的作法首先需要两个点确定一条直线,另外在直线外确定一点(即控制点),然后此时三点会形成三个线段,即下图的P0P2、P0P1和P1P2P_{0}P_{2}、P_{0}P_{1}和P_{1}P_{2}(其实不用关注 P0P2P_{0}P_{2})

这只是进度为0时候的状态,按照上面概念,当进度 tt 从 0 变化到 100 时的某一个时刻,比如 30, 66 ,99,那么各个时刻P0P1和P1P2P_{0}P_{1}和P_{1}P_{2}的状态为



可以发现,在P0P1和P1P2P_{0}P_{1}和P_{1}P_{2}上有一直运动的两个点,我们将这两个点连接起来又形成一段新的线段,而在不同时刻,在这个新线段上同样会有一个运动的点,这个点也遵守 tt 的变化。



把所有时刻的***点连接起来,就形成了二阶贝塞尔曲线。

还不能理解的可以看下这个视频 - > 《bezier curve原理》 只要看就好,听不懂英文的可以把声音关掉。
费这么大劲把二阶贝塞尔讲了一遍,我们这里其实也只用到了二阶,高阶我就不讲了,一通百通。
这个其实有点靠猜了=。= 一开始我觉得应该在连心线的中点,其实实现后效果也还行,后来参照腾讯设计师的想法效果更好,他令 P1P2P_{1}P_{2} 的控制点为 P1P4P_{1}P_{4} 的中点,令P3P4P_{3}P_{4} 的控制点为 P2P3P_{2}P_{3} 的中点。
软件实现效果对比(左边控制点是连心线的中点,右边是腾讯设计师提出的控制点):


我个人觉得右边效果更好,也不得不佩服TX设计师的聪明才智,让我自己想可能永远也想不到。
至于求 P1P4P_{1}P_{4} 和 P2P3P_{2}P_{3} 的中点不难吧?连四个坐标点都求出来了,直接算就可以了!
本文算法已经用程序验证过正确性,但是程序现在还太简单了,等我完善后再发出来!
References:
《QQ手机版 5.0“一键下班”设计小结》
《【Android开源项目解析】QQ“一键下班”功能实现解析——学习Path及贝塞尔曲线的基本使用》
Github - MetaballLoading
本教程为了方便讲解有篡改原图,还望原图作者见谅!

直到如今我还是觉得这个功能很酷炫!于是想自己实现一番,经过一番调查知道拉伸其实就是由两个圆加上两条贝塞尔曲线组成的形状。
来看看腾讯设计师是怎么设计出来的吧:《QQ手机版 5.0“一键下班”设计小结》
看完了这个对实现思路有很大的帮助,可是我还是不能知道具体是怎么计算实现的,网上大部分的教程都是假想成了两个同样大小的圆来计算,这太取巧了!因为同样大小的圆两条外公切线是平行的,同一个圆上的公切点相连是会垂直于连心线的,但是大小不同的圆并没有这个特殊性!
另外网上也有很多仿照的项目,可是看算法看得头都大了也不明白为什么是这样算的!经过两天的研究,把初中数学(圆、三角函数等相关知识)好好复习了一遍,终于搞清楚了其中算法,现在跟我一起来看看吧!
1.得到连心线
通过观察可以发现,在“一键退朝”这个功能当中,有一个小圆固定在原来坐标位置不动的,只是半径会发生变化,另一个大圆是跟随着我们手指滑动到屏幕的位置来确定圆心坐标的,一般大圆的半径是固定的。建立两圆的相对坐标系:

PS:在移动端的坐标系 yy 轴是向下的。
假设某一个时刻,两圆的状态如图,我们现在可以确定的是小圆的圆心坐标 OO 为(startXstartX, startYstartY),大圆的圆心坐标 P0P_{0} 为 (x0x_{0}, y0y_{0}),以及小圆的半径 rr 和大圆的半径 RR 。
那么首先可以把连心线求出来!也就是 OP0OP_{0} 的距离。
连心线的长度:d=(x0−startX)2+(y0−startY)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√连心线的长度:d = \sqrt{ (x_{0} - startX)^{2}+ (y_{0} - startY)^{2}}
2.求切点坐标
复习一下初中数学:两个外离的圆,一定有两条外公切线。若两圆半径相同,则两外公切线平行;否则相交于一点,且该点与两圆心在同一直线。
我们再作一张有公切线的图:

切点为 P1、P2、P3、P4P_{1}、P_{2}、P_{3}、P_{4},我们现在目的就要求出这四个点,然后就能够在程序中画出切线。
整个算法最难的地方恐怕就是求这四个点了,我们需要借助作图来帮助计算,这之前还需要先复习下定理:
圆心和切点的连线一定垂直于过该点的公切线
首先过小圆圆心 OO 作一条平行于 P1P2P_{1}P_{2} 的线,和 P0P2P_{0}P_{2} 相交于点 MM ,可以得到 P1OMP2P_{1}OMP_{2} 为一个矩形,则 P2M=P1O=rP_{2}M = P_{1}O = r ,又因为 P2P0=RP_{2}P_{0} = R ,所以 P0M=R−rP_{0}M = R-r ,那么
可求:sinγ=sin∠MOP0=MP0OP0=R−rd可求:sin\gamma = sin\angle MOP_{0} = \frac{MP_{0}}{OP_{0}} = \frac{R - r}{d}
即:γ=∠MOP0=arcsinR−rd即:\gamma = \angle MOP_{0} = arcsin \frac{R - r}{d}
作连心线和 xx 轴的夹角为 α \alpha
可求:tanα=startY−y0x0−startX可求: tan\alpha = \frac{startY - y_{0}}{x_{0} - startX}
即:∠α=arctanstartY−y0x0−startX即:\angle\alpha = arctan \frac{startY - y_{0}}{x_{0} - startX}
再作几个辅助点 A、B、C、DA、B、C、D,ABAB 表示以大圆圆心为原点的坐标系的 xx 轴的两端,CDCD 表示以小圆圆心为原点的坐标系的 xx 轴的两端,

∵AB//CD,∠P0OD=α∵AB // CD,\angle P_{0}OD = \alpha
∴∠AP0O=α∴\angle AP_{0}O = \alpha
∵∠P1OC=β,P1O//P2P0∵\angle P_{1}OC = \beta ,P_{1}O // P_{2}P_{0}
∴∠P2P0A=∠P1OC=β∴\angle P_{2}P_{0}A =\angle P_{1}OC = \beta
又∵OM⊥P2P0,得出∠OMP0=90°,即弧度值π2又∵OM \perp P_{2}P_{0} ,得出 \angle OMP_{0} = 90° ,即弧度值\frac{\pi}{2}
∴β=π2−γ−α∴\beta = \frac{\pi}{2} - \gamma - \alpha
现在 β\beta 求出来了,两圆的半径也已知,求 P1、P2P_{1}、P_{2} 的坐标是不是很简单?
综上:P1.x=startX−cosβ∗r,P1.y=startY−sinβ∗r综上:P_{1}.x = startX - cos\beta * r,P_{1}.y = startY - sin\beta * r
P2.x=x0−cosβ∗R,P1.y=y0−sinβ∗RP_{2}.x = x_{0}- cos\beta * R,P_{1}.y = y_{0} - sin\beta * R
3.求剩下两个切点的坐标
一开始我以为 P3、P4P_{3}、P_{4} 的算法和 P1、P2P_{1}、P_{2} 一样,就是把上面的减号换成加号就可以了。可是后来验证后发现不对, P3、P4P_{3}、P_{4} 不能直接使用 β\beta 进行运算。
为了能愉快阅读,再来复习一下各种拉丁希腊符号叫法:
α 阿尔法 β 贝塔 γ 伽玛 δ 德尔塔 ε 伊普西隆 ζ 泽塔
如上图作辅助线。
由于圆的对称性可知:∠P0ON=γ由于圆的对称性可知:\angle P_{0}ON = \gamma
∵δ+α=90°,即弧度值π2∵\delta + \alpha = 90°,即弧度值\frac{\pi}{2}
∴δ=π2−α∴\delta = \frac{\pi}{2} - \alpha
又∵ON⊥P0P4又∵ON \bot P_{0}P_{4}
∴γ+δ+ε=π2,即求出ε=π2−γ−δ∴\gamma +\delta + \varepsilon = \frac{\pi}{2},即求出\varepsilon = \frac{\pi}{2} -\gamma - \delta
又∵ε+ζ=π2又∵ \varepsilon + \zeta = \frac{\pi}{2}
综上,ζ=π2−ε=π2−(π2−γ−δ)=π2−(π2−γ−(π2−α))综上,\zeta = \frac{\pi}{2} - \varepsilon = \frac{\pi}{2} - (\frac{\pi}{2} -\gamma - \delta) = \frac{\pi}{2} - (\frac{\pi}{2} -\gamma - (\frac{\pi}{2} - \alpha))
即求出:ζ=π2+γ−α即求出:\zeta = \frac{\pi}{2} + \gamma - \alpha
在前面 γ\gamma 和 α\alpha 已经求出来了!那么 P4P_{4} 坐标也就不难了。
综上:P3.x=startX+cosζ∗r,P3.y=startY+sinζ∗r综上:P_{3}.x = startX + cos\zeta * r,P_{3}.y = startY + sin\zeta * r
P4.x=x0+cosζ∗R,P4.y=y0+sinζ∗RP_{4}.x = x_{0}+ cos\zeta * R,P_{4}.y = y_{0} + sin\zeta * R
4.画贝塞尔曲线
把四个切点坐标求出来了,后面就简单了,现在就是以切线为原轴,画贝塞尔曲线了,不过我们还缺少一个控制点的坐标。4.1 科普贝塞尔
怕有不清楚贝塞尔曲线的朋友,我科普一下先,简单来说就是求一段平滑曲线的公式。如果我们把画一条直线分为进度100%的话,那么当进度为0%,12%,58%,74%时,画线的状态为(注意红色部分末的黑色端点,灰色部分为路径指示)




那么把所有时刻的黑点连接起来就构成了直线:

这个概念应该比较容易接受,好了继续。
二次贝塞尔曲线(最简单的贝塞尔曲线)的作法首先需要两个点确定一条直线,另外在直线外确定一点(即控制点),然后此时三点会形成三个线段,即下图的P0P2、P0P1和P1P2P_{0}P_{2}、P_{0}P_{1}和P_{1}P_{2}(其实不用关注 P0P2P_{0}P_{2})

这只是进度为0时候的状态,按照上面概念,当进度 tt 从 0 变化到 100 时的某一个时刻,比如 30, 66 ,99,那么各个时刻P0P1和P1P2P_{0}P_{1}和P_{1}P_{2}的状态为



可以发现,在P0P1和P1P2P_{0}P_{1}和P_{1}P_{2}上有一直运动的两个点,我们将这两个点连接起来又形成一段新的线段,而在不同时刻,在这个新线段上同样会有一个运动的点,这个点也遵守 tt 的变化。



把所有时刻的***点连接起来,就形成了二阶贝塞尔曲线。

还不能理解的可以看下这个视频 - > 《bezier curve原理》 只要看就好,听不懂英文的可以把声音关掉。
费这么大劲把二阶贝塞尔讲了一遍,我们这里其实也只用到了二阶,高阶我就不讲了,一通百通。
4.2.寻找控制点
那么现在线段已经能确定了,就是两条公切线线段(P1P2、P3P4P_{1}P_{2}、P_{3}P_{4}),那么控制点在哪呢?这个其实有点靠猜了=。= 一开始我觉得应该在连心线的中点,其实实现后效果也还行,后来参照腾讯设计师的想法效果更好,他令 P1P2P_{1}P_{2} 的控制点为 P1P4P_{1}P_{4} 的中点,令P3P4P_{3}P_{4} 的控制点为 P2P3P_{2}P_{3} 的中点。

软件实现效果对比(左边控制点是连心线的中点,右边是腾讯设计师提出的控制点):


我个人觉得右边效果更好,也不得不佩服TX设计师的聪明才智,让我自己想可能永远也想不到。
至于求 P1P4P_{1}P_{4} 和 P2P3P_{2}P_{3} 的中点不难吧?连四个坐标点都求出来了,直接算就可以了!
本文算法已经用程序验证过正确性,但是程序现在还太简单了,等我完善后再发出来!
References:
《QQ手机版 5.0“一键下班”设计小结》
《【Android开源项目解析】QQ“一键下班”功能实现解析——学习Path及贝塞尔曲线的基本使用》
Github - MetaballLoading
本教程为了方便讲解有篡改原图,还望原图作者见谅!
相关文章推荐
- [项目实战派]触摸屏程序设计要点
- 添加dubbo监控
- 创建酷炫动画效果的10个JavaScript库
- AnjularJS跨域获取html页面
- Struts2 常用常量配置
- hdu 1800 (字符串哈希)
- #集合类-(数组)
- android开源框架
- ffmpeg
- 安卓加载大量图片
- apache的虚拟域名rewrite配置以及.htaccess的使用。
- Pomelo官方demo ChatofPomelo简析之一——用户登录
- java 内部类(第二讲 staitc)
- FMDB使用介绍
- iOS获取控制器里面的控件
- Spark-SQL优化案例---股票点击实时排行
- Weblogic 服务器SSL证书安装指南
- Spring Mvc学习笔记(一)续
- hive 空值的处理
- 【opencv交叉编译问题】用arm-linux-gnueabihf-gcc编译程序无法执行
