机器学习基石HOW部分(4)

机器学习基石HOW部分(4)

标签：机器学习基石

第十二章

nonlinear via nonlinear feature transform ϕ\phi plus linear with price of model complexity

前面的分析都是基于“线性假设“，它的优点是实际中简单有效，而且理论上有VC 维的保证；然而，面对线性不可分的数据时（实际中也有许多这样的例子），线性方法不那么有效。

比如下面的例子：



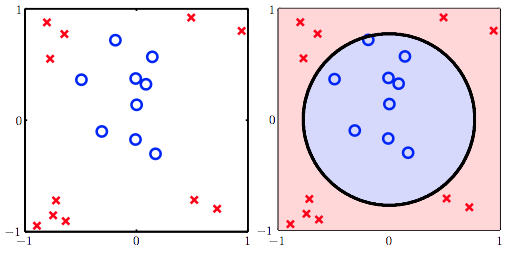
我们可以看出，二次曲线（比如圆）可以解决这个问题。

接下来就分析如何通过二次曲线假设解决线性方法无法处理的问题，进而推广到多次假设。

假设分类器是一个圆心在原点的正圆，圆内的点被分为+1，圆外的被分为-1，于是有：

hSEP(x)=sign(−x21−x22+0.6)h_{SEP}(x)=sign(−x_1^2−x_2^2+0.6)

把圆圈分类器的方程改写一下：

h(x)=(0.6.0⋅1+(−1).x21+(−1).x22)h(x)=(0.6 \quad. \quad 0⋅1+(−1)\quad. \quad x_1^2+(−1)\quad. \quad x_2^2)

=sign(w˜0+w˜1z1+w˜2z2)=sign(w˜Tz)=sign(\widetilde w_0+\widetilde w_1z_1+\widetilde w_2z_2)=sign(\widetilde w^Tz)

可以这样理解，原来的x 变量都映射到了z-空间，这样，在x-空间中线性不可分的数据，在z-空间中变得线性可分；然后，我们在新的z-空间中进行线性假设。



这个转换的过程成为nonlinear feature transform，用符号ϕ\phi表示，ϕ\phi把两个互相独立的空间给联系了起来:

(1,x21,x−22)=ϕ(x)=(z0,z1,z2)=z(1,x_1^2,x-2^2)=\phi (x)=(z_0,z_1,z_2)=z

X空间下的每个点，都对应Z空间下的某个点，同样的，X空间下的二次曲线方程，都对应Z空间下的某个一次直线方程。

h(x)=sign(w˜0+w˜1x21+w˜2x22)=sign(w˜Tϕ(x))=h˜(z)h(x)=sign(\widetilde w_0+\widetilde w_1x_1^2+\widetilde w_2x_2^2)=sign(\widetilde w^T\phi (x))=\widetilde h(z)

w˜\widetilde w	X空间下的曲线形态
(0.6,−1,−1)	circle(圈圈在内部，叉叉在外部)
(−0.6,+1,+1)	circle(圈圈在外部，叉叉在内部)
(0.6,−1,−2)	椭圆(ellipse)
(0.6,−1,+2)	双曲线(hyperbola)
(0.6,+1,+2)	所有点都判断为圈圈

上面的例子，它们的中心都必须在原点。

如果想要得到跟一般的二次曲线，如圆心不在原点的圆、斜的椭圆、抛物线等，则需要更一般的二次假设。

ϕ(x)=(1,x1,x2,x21,x1x2,x22)\phi (x)=(1,x_1,x_2,x_1^2,x_1x_2,x_2^2)

这样一来，这个完整版的Z空间的直线，就可以代表X空间下的所有二次曲线了。

非线性转换(nonlinear transform)

进行非线性转换的步骤（这里的非线性转换其实也是特征转换(feature transform)，在特征工程里很常见。）：

非线性变换的代价

所谓”有得必有失“，将特征转换到高次空间，我们需要付出学习代价（更高的模型复杂度）。

x-空间的数据转换到z-空间之后，新的假设中的参数数量也比传统线性假设多了许多

Q-th Order Polynomial Transform

d维向量x经过Q次多项式变换:

ϕ(x)=(1,\phi (x)=(1,

x1,x2,...,xd,x_1,x_2,...,x_d,

x21,x1x2,...,x2d,x^2_1,x_1x_2,...,x^2_d,

...,...,

xQ1,xQ−11x2,...,xQd)x^Q_1,x^{Q−1}_1x_2,...,x^Q_d)

根据之前分析过的，vc 维约等于自由变量（参数）的数量，所以新假设的dvcd_{vc} 急速变大，也就是模型复杂大大增加(复杂度由O(d)变为O(QdQ^d))。



上图是分别使用原始数据进行训练以及进行4次非线性变换后的数据进行训练的结果对比。从视觉上看，虽然右图(经过4次非线性变换的模型)能够把圈圈叉叉完全分开，但显然这种模型过于复杂了。

回顾机器学习前几讲的内容，我们可以有效学习的条件是：（1）Ein(g)E_{in}(g) 约等于Eout(g)E_{out}(g)；（2）Ein(g)E_{in}(g)足够小。

当模型很简单时（dvcd_{vc}很小），我们更容易满足（1）而不容易满足（2）；反之，模型很复杂时（dvcd_{vc}很大），更容易满足（2）而不容易满足（1）。

那么如何选择合适的复杂度呢？像上面一样用眼睛看？暂且不讨论10维的数据有没有办法用眼睛看，就拿前面2维的例子来说，用眼睛看来选择模型是件很危险的事情。

因为你是在“看过”数据之后，由你大脑选择的一个模型，这里要考虑到你大脑“选择模型”产生的一个复杂度，因为如果重新选取一部分数据，你有可能就不再挑选这个模型了，事实上你的大脑不知不觉地参与到了模型参数估计上。因此要切记，在ϕ\phi的选择之前，不可以偷偷去看数据。

假设集(Structured Hypothesis Sets)

前面我们分析的非线性转换都是多项式转换(polynomial transform)。

我们用符号ϕQ\phi Q来表示Q次多项式变换:

ϕ0(x)=(1),ϕ1(x)=(ϕ0(x),x1,x2……,xd)\phi _0(x)=(1),\phi _1(x) = (\phi _0(x),x_1,x_2……,x_d)

ϕ2(x)=(ϕ1x,x21,x1x2,……,x2d)\phi _2(x) = (\phi _1{x},x^2_1,x_1x_2,……,x^2_d)

…………

ϕQ(x)=(ϕQ−1(x),xQ1,xQ−11x2,...,xQd)\phi _Q(x)=(\phi _Q−1(x),x^Q_1,x^{Q−1}_1x_2,...,x^Q_d)

可以发现ϕi(x)\phi _i(x)中包含了ϕi−1(x)\phi _{i−1}(x)，因此他们对应的Hypothesis Set也有如下关系:

Hϕ0⊂Hϕ1⊂Hϕ2⊂……⊂HϕQH\phi _0 \subset H\phi _1 \subset H\phi _2 \subset …… \subset H\phi _Q

我们将二次假设记为H2H_2，k次假设记为HkH_k。显然，高次假设的模型复杂度更高。

H0⊂H1⊂H2⊂……⊂HQH _0 \subset H _1 \subset H _2 \subset …… \subset H _Q



也就是说，高次假设对数据拟合得更充分，EinE_{in} 更小；然而，由于付出的模型复杂度代价逐渐增加，EoutE_{out} 并不是一直随着EinE_{in}减小。



通常在进行高次非线性变换的时候，应该特别小心，因为dvcd_{vc}上升很快，极容易造成overfitting。比较安全的做法是，先尝试不做非线性变换，即使用Hϕ1H\phi _1，如果效果足够好了，就不需要进行非线性变换，否则，转而进行更高次的假设，一旦获得满意的Ein 就停止学习（不再进行更高次的学习）。

总结为一句话：linear/simpler model first !