数据结构实验之图论八:欧拉回路
2015-11-26 13:25
239 查看
无向图存在欧拉回路的充要条件
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。
有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路,所有顶点的入度等于出度且该图是连通图。
混合图存在欧拉回路条件
要判断一个混合图G(V,E)(既有有向边又有无向边)是欧拉图,方法如下:
假设有一张图有向图G',在不论方向的情况下它与G同构。并且G'包含了G的所有有向边。那么如果存在一个图G'使得G'存在欧拉回路,那么G就存在欧拉回路。
其思路就将混合图转换成有向图判断。实现的时候,我们使用网络流的模型。现任意构造一个G'。用Ii表示第i个点的入度,Oi表示第i个点的出度。如果存在一个点k,|Ok-Ik|mod 2=1,那么G不存在欧拉回路。接下来则对于所有Ii>Oi的点从源点连到i一条容量为(Ii-Oi)/2的边,对于所有Ii<Oi的点从i连到汇点一条容量为(Oi-Ii)/2的边。如果对于节点U和V,无向边(U,V)∈E,那么U和V之间互相建立容量为无限大的边。如果此网络的最大流等于∑|Ii-Oi|/2,那么就存在欧拉回路。
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。
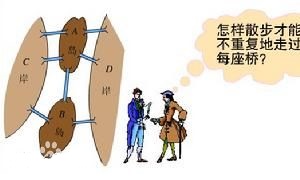
能否走过这样的七座桥,并且每桥只走一次?瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡七桥问题,并证明了更为广泛的有关一笔画的三条结论,人们通常称之为欧拉定理。对于一个连通图,通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。
你的任务是:对于给定的一组无向图数据,判断其是否成其为欧拉图?
连续T组数据输入,每组数据第一行给出两个正整数,分别表示结点数目N(1 < N <= 1000)和边数M;随后M行对应M条边,每行给出两个正整数,分别表示该边连通的两个结点的编号,结点从1~N编号。
若为欧拉图输出1,否则输出0。
如果无向图连通并且所有结点的度都是偶数,则存在欧拉回路,否则不存在。
xam
解法一:(并查集)
解法三:(BFS)
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。
有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路,所有顶点的入度等于出度且该图是连通图。
混合图存在欧拉回路条件
要判断一个混合图G(V,E)(既有有向边又有无向边)是欧拉图,方法如下:
假设有一张图有向图G',在不论方向的情况下它与G同构。并且G'包含了G的所有有向边。那么如果存在一个图G'使得G'存在欧拉回路,那么G就存在欧拉回路。
其思路就将混合图转换成有向图判断。实现的时候,我们使用网络流的模型。现任意构造一个G'。用Ii表示第i个点的入度,Oi表示第i个点的出度。如果存在一个点k,|Ok-Ik|mod 2=1,那么G不存在欧拉回路。接下来则对于所有Ii>Oi的点从源点连到i一条容量为(Ii-Oi)/2的边,对于所有Ii<Oi的点从i连到汇点一条容量为(Oi-Ii)/2的边。如果对于节点U和V,无向边(U,V)∈E,那么U和V之间互相建立容量为无限大的边。如果此网络的最大流等于∑|Ii-Oi|/2,那么就存在欧拉回路。
数据结构实验之图论八:欧拉回路
Time Limit: 1000MS Memory limit: 65536K
题目描述
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。
能否走过这样的七座桥,并且每桥只走一次?瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡七桥问题,并证明了更为广泛的有关一笔画的三条结论,人们通常称之为欧拉定理。对于一个连通图,通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。
你的任务是:对于给定的一组无向图数据,判断其是否成其为欧拉图?
输入
连续T组数据输入,每组数据第一行给出两个正整数,分别表示结点数目N(1 < N <= 1000)和边数M;随后M行对应M条边,每行给出两个正整数,分别表示该边连通的两个结点的编号,结点从1~N编号。
输出
若为欧拉图输出1,否则输出0。
示例输入
1 6 10 1 2 2 3 3 1 4 5 5 6 6 4 1 4 1 6 3 4 3 6
示例输出
1
提示
如果无向图连通并且所有结点的度都是偶数,则存在欧拉回路,否则不存在。
来源
xam
示例程序
解法一:(并查集)#include<stdio.h>
#include<string.h>
int d[1010],f[1010];
int t,n,m;
int find(int x)
{
if(x!=f[x])
f[x]=find(f[x]);
return f[x];
}
void check(int x,int y)
{
int fx=find(x);
int fy=find(y);
if(fx!=fy)
f[fx]=fy;
}
int solve()
{
int cnt=0;
for(int i=1; i<=n; ++i)
{
if(f[i]==i)
cnt++;
}
if(cnt!=1)
return 0;
for(int i=1;i<=n;++i)
{
if(d[i]%2==1)
return 0;
}
return 1;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
for(int i=1; i<=n; ++i)
{
f[i]=i;
d[i]=0;
}
int u,v;
for(int i=0; i<m; ++i)
{
scanf("%d%d",&u,&v);
check(u,v);
d[u]++;
d[v]++;
}
if(solve())
printf("1\n");
else
printf("0\n");
}
return 0;
}解法二:(DFS)#include<stdio.h>
#include<string.h>
int map[1010][1010],visited[10100],sum,d[2000],n;
void DFS(int x)
{
int i;
visited[x]=1;
sum++;
for(i=1;i<=n;i++)
if(visited[i]==0&&map[x][i])
DFS(i);
}
int main()
{
int i,j,m,k,t,l1,l2;
scanf("%d",&t);
while(t--)
{
sum=0;
memset(map,0,sizeof(map));
memset(visited,0,sizeof(visited));
memset(d,0,sizeof(d));
scanf("%d %d",&n,&m);
for(i=0;i<m;i++)
{
scanf("%d %d",&l1,&l2);
map[l1][l2]=1;
map[l2][l1]=1;
d[l1]++;
d[l2]++;
}
DFS(l1);
for(i=1;i<=n;i++)
if(d[i]%2==1)
break;
if(i==n+1&&sum==n)
printf("1\n");
else
printf("0\n");
}
}解法三:(BFS)
#include<stdio.h>
#include<string.h>
int map[1010][1010],visited[10100],sum,d[2000],d1[2000],n;
void BFS(int s)
{
int out=0,in=0,v,i;
visited[s]=1;
sum++;
d1[in++]=s;
while(out<in)
{
v=d1[out++];
for(i=1;i<=n;i++)
if(visited[i]==0&&map[v][i])
{
visited[i]=1;
sum++;
d1[in++]=i;
}
}
}
int main()
{
int i,j,m,k,t,l1,l2;
scanf("%d",&t);
while(t--)
{
sum=0;
memset(map,0,sizeof(map));
memset(visited,0,sizeof(visited));
memset(d,0,sizeof(d));
scanf("%d %d",&n,&m);
for(i=0;i<m;i++)
{
scanf("%d %d",&l1,&l2);
map[l1][l2]=1;
map[l2][l1]=1;
d[l1]++;
d[l2]++;
}
BFS(1);
for(i=1;i<=n;i++)
if(d[i]%2==1)
break;
if(i==n+1&&sum==n)
printf("1\n");
else
printf("0\n");
}
}
相关文章推荐
- 数据结构实验之图论四:迷宫探索
- 【数据结构】 栈的应用举例(3例)——更好的学习和理解栈
- 数据结构之二叉树详说
- 数据结构之堆(java)
- 数据结构实验之图论四:迷宫探索
- 【2015/11/21】 数据结构学习日志_Day17 双端链表
- leetcode之Rotate Array
- redis数据结构-链表
- 双向链表
- 数据结构与算法(4)--队列
- 机器学习模型数据结构:logistic regression, neural network, convolutional neural network
- 数据结构学习(C++)—二叉树
- 深度优先搜索——毕业BG
- 黑马程序员—Java基础—java基础语法:数据结构,运算符,选择结构,循环结构
- 数据结构基础6.3:最小生成树MST(Prim、Kruskal)
- 用c语言实现二分法查找表格【数据结构】
- 数据结构——建立单向链表(java实现)
- MySQL索引背后的数据结构及算法原理
- 二叉树
- 数据结构基础6.2:图的遍历
