LaTeX 中插入数学公式
2015-11-09 20:59
274 查看
一、常用的数学符号
1、小写希腊字母
2、大写希腊字母
大写希腊字母只需要将小写希腊字母的第一个英文字母大写即可。但是需要注意的是,有些小写希腊字母的大写可以直接通过键盘输入,也就是说和英文大写是相同的。
3、运算符
对于加减除,对应键盘上便可打出来,但是对于乘法,键盘上没有这个符号,所以我们应该输入 \times 来显示一个
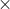
号。
普通字符在数学公式中含义一样,除了 # $ % & ~ _ ^ \ { } 若要在数学环境中表示这些符号# $ % & _ { },需要分别表示为\# \$ \% \& \_ \{ \},即在个字符前加上\。
二、简单格式
1、上下标
上标:$ f(x) = x^2 $ 或者 $ f(x) = {x}^{2} $ 均可表示
%3dx%5e2)
。
下标:$ f(x) = x_2 $ 或者 $ f(x) = {x}_{2} $ 均可表示
%3dx_2)
。
上下标可以级联:$ f(x) = x_1^2 + {x}_{2}^{2} $
%3dx_1%5e2%2b%7bx%7d_%7b2%7d%5e%7b2%7d)
。
2、加粗和倾斜
加粗:$ f(x) = \textbf{x}^2 $
%3d%5ctextbf%7bx%7d%5e2)
。
文本:$ f(x) = x^2 \mbox{abcd} $
%3dx%5e2%5cmbox%7babcd%7d)
倾斜:$ f(x) = x^2 \mbox{\emph{abcd} defg} $
%3dx%5e2%5cmbox%7b%5cemph%7babcd%7ddefg%7d)
3、分数
%3d%5cfrac%7bx%5e2%7d%7by%5e3%7d)
4、开根号
%3d%5csqrt%5bn%5d%7bx%5e2y%5e3%7d)
5、省略号
%3dx_1%2bx_2%2b%5ccdots%2bx_n)
6、括号和分隔符
公式高度比较低的话直接从键盘输入括号即可,但是对于公式高度比较高的情形,需要特殊的运算。
%3d(%5cfrac%7bdf%7d%7bdx%7d))
%3d%5cleft(%5cfrac%7bdf%7d%7bdx%7d%5cright))
可以看出,通过将 \left( 和 \right) 结合使用,可以将括号大小随着其内容变化。[ ] 和 { } 同理。
%3d%5cleft.%5cfrac%7bdf%7d%7bdx%7d%5cright%7c_%7bx%3d0%7d)
三、矩阵和行列式
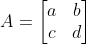
%3d%5cleft%7c%5cbegin%7bmatrix%7d%0a%5clambda-a%26-b%5c%5c%0a-c%26%5clambda-d%5c%5c%0a%5cend%7bmatrix%7d%5cright%7c)
四、求和与连乘
)
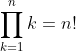
五、导数、极限、积分
1、导数
导数的表示用一对花括号将被导函数括起来,然后加上一个英文的引号即可。
%3dx%5e2%2bx)
2、极限
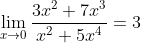
3、积分
积分中,需要注意的是,在多重积分内 dx 和 dy 之间 使用一个斜杠加一个逗号 \, 来增大稍许间距。同样,在两个积分号之间使用一个斜杠加一个感叹号 \! 来减小稍许间距。使之更美观。
%5c%2cdx)
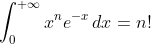
%5c%2cdx%5c%2cdy%c2%a0%3d%c2%a0%5cint_%7b%5ctheta%3d0%7d%5e%7b2%5cpi%7d%c2%a0%5cint_%7br%3d0%7d%5eR%c2%a0f(r%5ccos%5ctheta%2cr%5csin%5ctheta)%c2%a0r%5c%2cdr%5c%2cd%5ctheta)
%5c%2cdx%5c%2cdy%0a%5cint%c2%a0%5cint_D%c2%a0f(x%2cy)%5c%2cdx%5c%2cdy)
在加入了 \! 之后,距离的改变还是很明显的。
%c2%a0%5cpsi%c2%a0%2b%c2%a0V%c2%a0%5cpsi)
%5cright%7c%5e2%5c%2cdx%5c%2cdy%5c%2cdz%3d0)
1、小写希腊字母
| \alpha | \nu | ||
| \beta | \xi | ||
| \gamma | o | ||
| \delta | \pi | ||
| \epsilon | \rho | ||
| \zeta | \sigma | ||
| \eta | \tau | ||
| \theta | \upsilon | ||
| \iota | \phi | ||
| \kappa | \chi | ||
| \lambda | \psi | ||
| \mu | \omega |
大写希腊字母只需要将小写希腊字母的第一个英文字母大写即可。但是需要注意的是,有些小写希腊字母的大写可以直接通过键盘输入,也就是说和英文大写是相同的。
| \Gamma | \Lambda | ||
| \Sigma | \Psi | ||
| \Delta | \Upsilon | ||
| \Omega | \Theta | ||
| \Xi | \Pi | ||
| \Phi |
对于加减除,对应键盘上便可打出来,但是对于乘法,键盘上没有这个符号,所以我们应该输入 \times 来显示一个
号。
普通字符在数学公式中含义一样,除了 # $ % & ~ _ ^ \ { } 若要在数学环境中表示这些符号# $ % & _ { },需要分别表示为\# \$ \% \& \_ \{ \},即在个字符前加上\。
二、简单格式
1、上下标
上标:$ f(x) = x^2 $ 或者 $ f(x) = {x}^{2} $ 均可表示
。
下标:$ f(x) = x_2 $ 或者 $ f(x) = {x}_{2} $ 均可表示
。
上下标可以级联:$ f(x) = x_1^2 + {x}_{2}^{2} $
。
2、加粗和倾斜
加粗:$ f(x) = \textbf{x}^2 $
。
文本:$ f(x) = x^2 \mbox{abcd} $
倾斜:$ f(x) = x^2 \mbox{\emph{abcd} defg} $
3、分数
$ f(x,y) = \frac{x^2}{y^3} $4、开根号
$ f(x,y) = \sqrt
{{x^2}{y^3}} $5、省略号
$ f(x_1, x_2, \ldots, x_n) = x_1 + x_2 + \cdots + x_n $
6、括号和分隔符
公式高度比较低的话直接从键盘输入括号即可,但是对于公式高度比较高的情形,需要特殊的运算。
$ {f}'(x) = (\frac{df}{dx}) $$ {f}'(x) = \left( \frac{df}{dx} \right) $可以看出,通过将 \left( 和 \right) 结合使用,可以将括号大小随着其内容变化。[ ] 和 { } 同理。
$ {f}'(0) = \left. \frac{df}{dx} \right|_{x=0} $三、矩阵和行列式
$ A=\left[ \begin{matrix}
a & b \\
c & d \\
\end{matrix} \right] $$ \chi (\lambda)=\left| \begin{matrix}
\lambda - a & -b \\
-c & \lambda - d \\
\end{matrix} \right| $四、求和与连乘
$ \sum_{k=1}^n k^2 = \frac{1}{2} n (n+1) $$ \prod_{k=1}^n k = n! $五、导数、极限、积分
1、导数
导数的表示用一对花括号将被导函数括起来,然后加上一个英文的引号即可。
$ {f}'(x) = x^2 + x $2、极限
$ \lim_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3 $3、积分
积分中,需要注意的是,在多重积分内 dx 和 dy 之间 使用一个斜杠加一个逗号 \, 来增大稍许间距。同样,在两个积分号之间使用一个斜杠加一个感叹号 \! 来减小稍许间距。使之更美观。
$ \int_a^b f(x)\,dx $
$ \int_0^{+\infty} x^n e^{-x} \,dx = n! $$ \int_{x^2 + y^2 \leq R^2} f(x,y)\,dx\,dy = \int_{\theta=0}^{2\pi} \int_{r=0}^R f(r\cos\theta,r\sin\theta) r\,dr\,d\theta $$ \int \!\!\! \int_D f(x,y)\,dx\,dy \int \int_D f(x,y)\,dx\,dy $
在加入了 \! 之后,距离的改变还是很明显的。
$ i\hbar\frac{\partial \psi}{\partial {t}} = \frac{-\hbar^2}{2m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) \psi + V \psi $$ \frac{d}{dt} \int \!\!\! \int \!\!\! \int_{\textbf{R}^3} \left| \psi(\mathbf{r},t) \right|^2\,dx\,dy\,dz = 0 $相关文章推荐
- Linux 查看设置系统语言
- [置顶] 新博客
- 什么叫有源滤波电路 什么叫无源滤波 分别是怎样定义的?
- Spring之—— AspectJ AOP 完整示例
- 解决使用百度地图默认定位是北京的问题
- POI导出JavaWeb中的table到excel下载 (很通用)
- xmlpullparser用法体会
- iOS app上传问题
- echo(),print(),print_r()之间的区别?
- 【Codeforces Round 324 (Div 2)E】【贪心 构造】Anton and Ira 全排列交换 最小距离成本
- 黄山自驾游攻略——不仅仅是攻略哦
- Android编译和运行原理
- Java基础--serialVersionUID
- 活动选择问题 (动态规划、贪心算法)
- Opencv学习手册(二)--- 图像采集与显示
- 剑指Offer-12-打印1到最大的n位数
- Android各种分辨率
- WIN7快捷键列表
- 1100. Mars Numbers
- 最大流/最小割(maxflow/mincut)的原理讲解和代码实现
