动态规划(1)
2015-11-03 20:07
281 查看
近年来,涉及动态规划的各种竞赛题越来越多,每一年的NOI几乎都至少有一道题目需要用动态规划的方法来解决;而竞赛对选手运用动态规划知识的要求也越来越高,已经不再停留于简单的递推和建模上了。要了解动态规划的概念,首先要知道什么是多阶段决策问题。
如果一类活动过程可以分为若干个互相联系的阶段,在每一个阶段都需作出决策(采取措施),一个阶段的决策确定以后,常常影响到下一个阶段的决策,从而就完全确定了一个过程的活动路线,则称它为多阶段决策问题。
各个阶段的决策构成一个决策序列,称为一个策略。每一个阶段都有若干个决策可供选择,因而就有许多策略供我们选取,对应于一个策略可以确定活动的效果,这个效果可以用数量来确定。策略不同,效果也不同,多阶段决策问题,就是要在可以选择的那些策略中间,选取一个最优策略,使在预定的标准下达到最好的效果.
让我们先来看下面的例子:如图所示的是一个带权有向的多段图,要求从A到D的最短路径的长度(下面简称最短距离)。
我们可以搜索,枚举图中的每条路径,但当图的规模大起来时,搜索的效率显然不可能尽人意。让我们来试用动态规划的思路分析这道题:从图中可以看到,A点要到达D点必然要经过
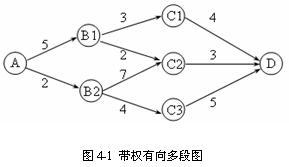
B1和B2中的一个,所以A到D的最短距离必然等于B1到D的最短距离加上5,或是B2到D的最短 距离加上2。同样的,B1到D的最短距离必然等于C1到D的最短距离加上3或是C2到D的最短距离加上2,……。
我们设G[i]为点i到点D的距离,显然G[C1]=4,G[C2]=3,G[C3]=5,根据上面的分析,有:
G[B1]=min{G[C1]+3,G[C2]+2}=5,
G[B2]=min{G[C2]+7,G[C3]+4}=9,
再就有G[A]=min{G[B1]+5,G[B2]+2}=10,
所以A到D的最短距离是10,最短路径是AB1C2D。
二、动态规划的术语
1.阶段
把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同.描述阶段的变量称为阶段变量。在前面的例子中,第一个阶段就是点A,而第二个阶段就是点A到点B,第三个阶段是点B到点C,而第四个阶段是点C到点D。
2.状态
状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。在上面的例子中状态就是某阶段的出发位置,它既是该阶段某路的起点,同时又是前一阶段某支路的终点。
在前面的例子中,第一个阶段有一个状态即A,而第二个阶段有两个状态B1和B2,第三个阶段是
4000
三个状态C1,C2和C3,而第四个阶段又是一个状态D。状态通常可以用一个或一组数来描述,称为状态变量。
3.无后效性
我们要求状态具有下面的性质:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响,所有各阶段都确定时,整个过程也就确定了。换句话说,过程的每一次实现可以用一个状态序列表示,在前面的例子中每阶段的状态是该线路的始点,确定了这些点的序列,整个线路也就完全确定。从某一阶段以后的线路开始,当这段的始点给定时,不受以前线路(所通过的点)的影响。状态的这个性质意味着过程的历史只能通过当前的状态去影响它的未来的发展,这个性质称为无后效性。
4.决策
一个阶段的状态给定以后,从该状态演变到下一阶段某个状态的一种选择(行动)称为决策。在许多问题中,决策可以自然而然地表示为一个数或一组数。不同的决策对应着不同的数值。描述决策的变量称决策变量,因状态满足无后效性,故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史。
5.策略
由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程,可供选取的策略有一定的范围限制,这个范围称为允许策略集合。允许策略集合中达到最优效果的策略称为最优策略。
给定k阶段状态变量x(k)的值后,如果这一阶段的决策变量一经确定,第k+1阶段的状态变量x(k+1)也就完全确定,即x(k+1)的值随x(k)和第k阶段的决策u(k)的值变化而变化,那么可以把这一关系看成(x(k),u(k))与x(k+1)确定的对应关系,用x(k+1)=Tk(x(k),u(k))表示。这是从k阶段到k+1阶段的状态转移规律,称为状态转移方程。
6.最优性原理
作为整个过程的最优策略,它满足:相对前面决策所形成的状态而言,余下的子策略必然构成“最优子策略”。最优性原理实际上是要求问题的最优策略的子策略也是最优。让我们通过对前面的例子再分析来具体说明这一点:从A到D,我们知道,最短路径是AB1C2D,这些点的选择构成了这个例子的最优策略,根据最优性原理,这个策略的每个子策略应是最优:AB1C2是A到C2的最短路径,B1C2D也是B1到D的最短路径……事实正是如此,因此我们认为这个例子满足最优性原理的要求。
下面给几个例子:
例1、数字三角形
如下所示为一个数字三角形.请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字的总和最大.只要求输出总和.
■ 每一步可沿左斜线向下或右斜线向下走;
■ 三角形行数小于等于100;
■ 三角形中的数字为0,1,……,99;
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
结果为:
30
7
3
8
7
5
例2:最长不下降序列(HNOI 1997)
一、问题描述
设有整数序列b1,b2,b3,…,bm,若存在i1
倒推:
例3:01背包问题
在M件物品取出若干件放在承重为W的背包里,每件物品的重量为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。
注意:在本题中,所有的重量值均为整数。
例如:背包最大承重为10 ,可放5件物品,其重量和价值分别为
物1 物2 物3 物4 物5
重量 2 4 3 3 6
价值 5 3 7 2 5
结果为:
10
1 2 4
[算法分析]:
阶段:在前N件物品中,选取若干件物品放入背包中;
状态:在前N件物品中,选取若干件物品放入所剩空间为W的背包中的所能获得的最大价值;
决策:第N件物品放或者不放;
状态转移方程:f[i,j]=max{f[i-1,j-Wi]+Pi (j>=Wi), f[i-1,j]}
我们用f[i,j]表示在前 i 件物品中选择若干件放在所剩空间为 j 的背包里所能获得的最大价值
算法设计如下:
例4:无限背包问题
在M种物品(每种物品有无限多个),取出若干件放在承重为W的背包里,每件物品的重量为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。 注意:在本题中,所有的重量值均为整数。
例如:背包最大承重为20 ,有5种物品的无限多个可放入,其重量和价值分别为
物1 物2 物3 物4 物5
重量 2 4 3 3 6
价值 5 3 7 2 5
(2)算法分析
•记F(K,Y)为取前K种物品,限制重量为Y时取得价值最大,则:
F(0,Y)=0,即对一切Y,一件物品都不取时,最大价值为0;
F(k,0)=0,即最大重量限制为0时,不能取得任何物品,所以最大价值也为0;
F(1,Y)=[y/w1]u1,即仅取第一种物品,则最大价值为尽可能多的装第一种物品,所以能装的数量为[y/w1],而得到的价值为[y/w1]u1。
一般公式:F(K,Y)=max{ F(K-1,Y),F(K,Y-Wk)+Vk}
下面用一个具体的例子来说明求解的过程。
N=4,XK=10
W1=2,W2=3,W3=4,W4=7
V1=1,V2=3,V3=5,V4=9
下面列出F(K,Y):
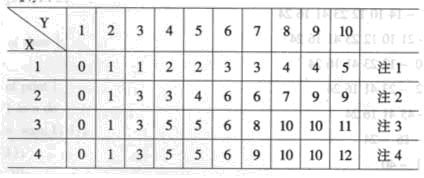
注1•第1行表示k=1,即取第一种物品,当Y=l时,无法取,所以F(1,1)=0,当y=2时,可取1个第一种物品,价值为1,…,当y=10(即XK),此时,可取5个第一种物品,价值为5。
注2•当可以取2种物品时。
当y=1时,为0(什么都不能取);
当y=2时,仅能取第一种物品,所以F(2,2)=1;
当y=3时,有2种取法。取一个第一种物品,价值为1;取一个第二种物品,价值为3,取大者,所以F(2,3)=3。
当y=4也有2种取法,取第一种物品2件,价值为2;取第二种物品1件价值为3,所以F(2,4)=3。
当y=5时,有2种取法,取第一种物品2件,价值为2;取第一种物品,第二种物品各1件,价值为4,所以F(2,5)=4。以此类推。计算F(2,10)时,有2种考虑,第一种是全部取第一种,即F(1,10)=5;第二种是由F(2,7)+3=6+9,取大者,得到F(2,10)=9。
注3•
注4•F(4,10)的计算方法为:
上面给出的是计算F(I,J)的方法,但是还不能确定每种物品的选取个数。下面我们用倒推法来求出每种物品的个数。
记F(N,XK)为目标,检查:F(N-1,Xk)与F(N,Xk-Wn)+Vn
若前者大,则无输出,由F(N,Xk)-> F(N-1,Xk。
若后者大,则输出WN,计算F(N,Xk-Wn)。
当N-1,N-2,…,到达1时,则全部输出。
(3)程序清单
INPUT:
4 10
2 3 4 7
1 3 5 9
OUTPUT:
N=: 4 XK=: 10
MAX WORTH = 12
NO: 1 WEIGHT: 2 WORTH: 1 GET: 0
NO: 2 WEIGHT: 3 WORTH: 3 GET: 1
NO: 3 WEIGHT: 4 WORTH: 5 GET: 0
NO: 4 WEIGHT: 7 WORTH: 9 GET: 1
例5:四塔问题
设有A,B,C,D四个柱子(有时称塔),在A柱上有由小到大堆放的n个盘子,如图所示。

今将A柱上的盘子移动到D柱上去。可以利用B,C柱作为工作栈用,移动的规则如下:
①每次只能移动一个盘子。
②在移动的过程中,小盘子只能放到大盘子的上面。
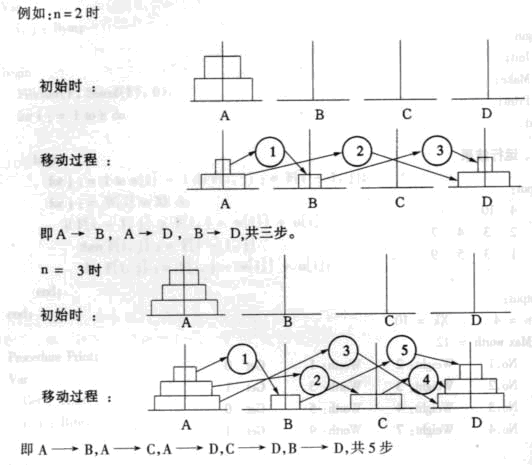
③下面给出盘子的个数为n的一般方法,用F4(n,a,b,c,d)表示四塔问题,从A到D移动n个盘子,可以利用b,c作为工作单元,四塔问题可以分解为:
F4(n,a,b,c,d)=>F4(r,a,c,d,b)+F3(n-r,a,c,d)+ F4(r,c,a,b,d)
即如何选择r使F4(n,a,b,c,d)为最小。r的取值范围为1,2,…,n-1,为此,我们构造2个整型数组:
F3(N),F4(N),其中F3用来存放三塔问题的解。
状态转移方程为:f4
:=min{2*f4[r]+f3[n-r],1<=r<=n-1}
(3)程序清单(高精度处理)
(INPUT N:10 TOTAL=49
INPUT N:1000 TOTAL=932385860354049)
例6:最小代价
(1)问题描述
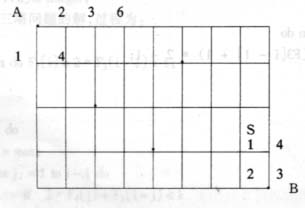
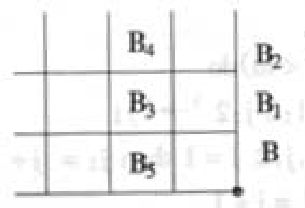
设有一个N*M的方格如图所示,在方格中去掉某些点,方格边上的数字代表距离,试找出一条从A到B的路径,经过的距离和为最小(此时称为最小代价),从A前进的方向只能向右,或向下,而被去掉点的代价可看成无穷大。
(2)算法分析
采用动态规划的方法,从B向A方向推导:
当路径到达B1之后,下面仅有一条通路B1->B。而最小距离为B1B。同样,当路径到达B5之后,下面仅有一条通路B5->B,而最小距离为B5B,但当路径达到B3时,有2条通路,B3B1,B1B,或B3B5,B5B,而最小路径为min{B3B+B1最小路径,B3B5+B5最小路径}。通常在方格中某个坐标点(i,i),其最小路径为:
min{(I,J)-(I,J+1)+(I,J+1)最小路径,(I,J)->(I+1,J)+(I+1,J)的最小路径}。为了记录求出的路径,用数组D(N,M,2)来记录,其中:
D(I,J,1)表示最小路径,D(I,J,2)表示下达的方向,1—-向右,2—-向下。
而约定D(N,M,1)=0,D(N,M,2)=0。

(3)程序清单
INPUT:
4 4
10 3 4 7
1 11 0 2
5 5 8 4
0 6 6 5
OUTPUT:
(1,1)–>(1,2)–>(1,3)–>(1,4)–>(2,4)–>(3,4)–>(4,4)
MIN COST = 30
二、练习题
1、扫雷
在一条河堤上有若干个地雷坑,每个地雷坑中埋有一定数量的地雷,地雷坑的编号为1,2,3,……,n(n<=100),如图(n=10)
地雷坑号 1 2 3 4 5 6 7 8 9 10
地雷数量 8 14 2 17 33 26 15 17 19 16
同时在每个地雷坑中都有一张说明书(除最后一个地雷除外),说明书指出,在挖完此坑的地雷后,还可以继续挖哪些坑。
挖地雷的规则是可以从任何一个地雷坑开始,到任何一个地雷坑结束,同时,在挖完某个地雷坑中的地雷后,可以选择它后面可继续挖的地雷坑这一继续挖,但只能选择一种。
问题:当地雷坑中的地雷数及后继关系给定后,找出一个挖地雷的方法,能挖到最多的地雷。(先给出状态转移方程,再写程序)
2、机器分配(HNOI’95)
总公司拥有高效生产设备M台,准备分给下属的N个公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M《=15,N〈=10。分配原则:每个公司有权获得任意数目的设备,但总台数不得超过总设备数M。保存数据的文件名从键盘输入。
数据文件格式为:第一行保存两个数,第一个数是设备台数M,第二个数是分公司数N。接下来是一个M*N的矩阵,表明了第I个公司分配J台机器的盈利。
(先给出状态转移方程,再写程序)
动态规划基本原理
一、多阶段决策问题如果一类活动过程可以分为若干个互相联系的阶段,在每一个阶段都需作出决策(采取措施),一个阶段的决策确定以后,常常影响到下一个阶段的决策,从而就完全确定了一个过程的活动路线,则称它为多阶段决策问题。
各个阶段的决策构成一个决策序列,称为一个策略。每一个阶段都有若干个决策可供选择,因而就有许多策略供我们选取,对应于一个策略可以确定活动的效果,这个效果可以用数量来确定。策略不同,效果也不同,多阶段决策问题,就是要在可以选择的那些策略中间,选取一个最优策略,使在预定的标准下达到最好的效果.
让我们先来看下面的例子:如图所示的是一个带权有向的多段图,要求从A到D的最短路径的长度(下面简称最短距离)。
我们可以搜索,枚举图中的每条路径,但当图的规模大起来时,搜索的效率显然不可能尽人意。让我们来试用动态规划的思路分析这道题:从图中可以看到,A点要到达D点必然要经过

B1和B2中的一个,所以A到D的最短距离必然等于B1到D的最短距离加上5,或是B2到D的最短 距离加上2。同样的,B1到D的最短距离必然等于C1到D的最短距离加上3或是C2到D的最短距离加上2,……。
我们设G[i]为点i到点D的距离,显然G[C1]=4,G[C2]=3,G[C3]=5,根据上面的分析,有:
G[B1]=min{G[C1]+3,G[C2]+2}=5,
G[B2]=min{G[C2]+7,G[C3]+4}=9,
再就有G[A]=min{G[B1]+5,G[B2]+2}=10,
所以A到D的最短距离是10,最短路径是AB1C2D。
二、动态规划的术语
1.阶段
把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同.描述阶段的变量称为阶段变量。在前面的例子中,第一个阶段就是点A,而第二个阶段就是点A到点B,第三个阶段是点B到点C,而第四个阶段是点C到点D。
2.状态
状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。在上面的例子中状态就是某阶段的出发位置,它既是该阶段某路的起点,同时又是前一阶段某支路的终点。
在前面的例子中,第一个阶段有一个状态即A,而第二个阶段有两个状态B1和B2,第三个阶段是
4000
三个状态C1,C2和C3,而第四个阶段又是一个状态D。状态通常可以用一个或一组数来描述,称为状态变量。
3.无后效性
我们要求状态具有下面的性质:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响,所有各阶段都确定时,整个过程也就确定了。换句话说,过程的每一次实现可以用一个状态序列表示,在前面的例子中每阶段的状态是该线路的始点,确定了这些点的序列,整个线路也就完全确定。从某一阶段以后的线路开始,当这段的始点给定时,不受以前线路(所通过的点)的影响。状态的这个性质意味着过程的历史只能通过当前的状态去影响它的未来的发展,这个性质称为无后效性。
4.决策
一个阶段的状态给定以后,从该状态演变到下一阶段某个状态的一种选择(行动)称为决策。在许多问题中,决策可以自然而然地表示为一个数或一组数。不同的决策对应着不同的数值。描述决策的变量称决策变量,因状态满足无后效性,故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史。
5.策略
由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程,可供选取的策略有一定的范围限制,这个范围称为允许策略集合。允许策略集合中达到最优效果的策略称为最优策略。
给定k阶段状态变量x(k)的值后,如果这一阶段的决策变量一经确定,第k+1阶段的状态变量x(k+1)也就完全确定,即x(k+1)的值随x(k)和第k阶段的决策u(k)的值变化而变化,那么可以把这一关系看成(x(k),u(k))与x(k+1)确定的对应关系,用x(k+1)=Tk(x(k),u(k))表示。这是从k阶段到k+1阶段的状态转移规律,称为状态转移方程。
6.最优性原理
作为整个过程的最优策略,它满足:相对前面决策所形成的状态而言,余下的子策略必然构成“最优子策略”。最优性原理实际上是要求问题的最优策略的子策略也是最优。让我们通过对前面的例子再分析来具体说明这一点:从A到D,我们知道,最短路径是AB1C2D,这些点的选择构成了这个例子的最优策略,根据最优性原理,这个策略的每个子策略应是最优:AB1C2是A到C2的最短路径,B1C2D也是B1到D的最短路径……事实正是如此,因此我们认为这个例子满足最优性原理的要求。
下面给几个例子:
例1、数字三角形
如下所示为一个数字三角形.请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字的总和最大.只要求输出总和.
■ 每一步可沿左斜线向下或右斜线向下走;
■ 三角形行数小于等于100;
■ 三角形中的数字为0,1,……,99;
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
结果为:
30
7
3
8
7
5
program st; var i,j,n:integer; a:array[1..100,1..100] of integer; f,g:array[1..100,1..100] of longint; begin read(n); for i:=1 to n do for j:=1 to i do read(a[i,j]); for i:=1 to n do f[n,i]:=a[n,i]; fillchar(g,sizeof(g),0); for i:=n-1 downto 1 do for j:=1 to i do if f[i+1,j]>f[i+1,j+1] then begin f[i,j]:=f[i+1,j]+a[i,j];g[i,j]:=0 end else begin f[i,j]:=f[i+1,j+1]+a[i,j];g[i,j]:=1 end; writeln(f[1,1]);writeln(a[1,1]); i:=1;j:=1; while i<n do begin if g[i,j]=1 then inc(j); inc(i); writeln(a[i,j]); end; end.
例2:最长不下降序列(HNOI 1997)
一、问题描述
设有整数序列b1,b2,b3,…,bm,若存在i1
read(n); for i:=1 to n do read(a[i]); for i:=2 to n do begin max:=0; for j:=1 to i-1 do if (a[j]<=a[i]) and (f[j]>max) then max:=f[j]; f[i]:=max+1; end; max:=0; for i:=1 to n do if max<f[i] then begin max:=f[i];k:=i end; writeln(max);
倒推:
read(n); for i:=1 to n do read(a[i]); f[n,1]:=1; for i:=1 to n do f[i,2]:=0; for i:=n-1 downto 1 do begin max:=0; for j:=i+1 to n do if (a[i]<=a[j]) and (f[j,1]>max) then begin max:=f[j,1];k:=j end; f[i,1]:=max+1;f[i,2]:=k; end; max:=0; for i:=1 to n do if max<f[i,1] then begin max:=f[i,1];k:=i end; writeln(max); while k<>0 do begin write(a[k],' '); k:=f[k,2]; end;
例3:01背包问题
在M件物品取出若干件放在承重为W的背包里,每件物品的重量为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。
注意:在本题中,所有的重量值均为整数。
例如:背包最大承重为10 ,可放5件物品,其重量和价值分别为
物1 物2 物3 物4 物5
重量 2 4 3 3 6
价值 5 3 7 2 5
结果为:
10
1 2 4
[算法分析]:
阶段:在前N件物品中,选取若干件物品放入背包中;
状态:在前N件物品中,选取若干件物品放入所剩空间为W的背包中的所能获得的最大价值;
决策:第N件物品放或者不放;
状态转移方程:f[i,j]=max{f[i-1,j-Wi]+Pi (j>=Wi), f[i-1,j]}
我们用f[i,j]表示在前 i 件物品中选择若干件放在所剩空间为 j 的背包里所能获得的最大价值
算法设计如下:
read(m,w); for i:=1 to m do read(v[i],p[i]); for i:=0 to w do f[0,i]:=0; for i:=1 to m do for j:=0 to w do begin f[i,j]:=f[i-1,j]; if (j>=v[i]) and (f[i-1,j-v[i]]+p[i]>f[i,j]) then f[i,j]:=f[i-1,j-v[i]]+p[i]; end; writeln(f[m,w]); I:=m;j:=w; While i>0 do Begin if f[I,j]<>f[i-1,j] then begin j:=j-v[i]; get[i]:=1; end; Dec(i); end; For i:=1 to m do If get[i]=1 then write(I,' ');
例4:无限背包问题
在M种物品(每种物品有无限多个),取出若干件放在承重为W的背包里,每件物品的重量为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。 注意:在本题中,所有的重量值均为整数。
例如:背包最大承重为20 ,有5种物品的无限多个可放入,其重量和价值分别为
物1 物2 物3 物4 物5
重量 2 4 3 3 6
价值 5 3 7 2 5
(2)算法分析
•记F(K,Y)为取前K种物品,限制重量为Y时取得价值最大,则:
F(0,Y)=0,即对一切Y,一件物品都不取时,最大价值为0;
F(k,0)=0,即最大重量限制为0时,不能取得任何物品,所以最大价值也为0;
F(1,Y)=[y/w1]u1,即仅取第一种物品,则最大价值为尽可能多的装第一种物品,所以能装的数量为[y/w1],而得到的价值为[y/w1]u1。
一般公式:F(K,Y)=max{ F(K-1,Y),F(K,Y-Wk)+Vk}
下面用一个具体的例子来说明求解的过程。
N=4,XK=10
W1=2,W2=3,W3=4,W4=7
V1=1,V2=3,V3=5,V4=9
下面列出F(K,Y):

注1•第1行表示k=1,即取第一种物品,当Y=l时,无法取,所以F(1,1)=0,当y=2时,可取1个第一种物品,价值为1,…,当y=10(即XK),此时,可取5个第一种物品,价值为5。
注2•当可以取2种物品时。
当y=1时,为0(什么都不能取);
当y=2时,仅能取第一种物品,所以F(2,2)=1;
当y=3时,有2种取法。取一个第一种物品,价值为1;取一个第二种物品,价值为3,取大者,所以F(2,3)=3。
当y=4也有2种取法,取第一种物品2件,价值为2;取第二种物品1件价值为3,所以F(2,4)=3。
当y=5时,有2种取法,取第一种物品2件,价值为2;取第一种物品,第二种物品各1件,价值为4,所以F(2,5)=4。以此类推。计算F(2,10)时,有2种考虑,第一种是全部取第一种,即F(1,10)=5;第二种是由F(2,7)+3=6+9,取大者,得到F(2,10)=9。
注3•
注4•F(4,10)的计算方法为:
上面给出的是计算F(I,J)的方法,但是还不能确定每种物品的选取个数。下面我们用倒推法来求出每种物品的个数。
记F(N,XK)为目标,检查:F(N-1,Xk)与F(N,Xk-Wn)+Vn
若前者大,则无输出,由F(N,Xk)-> F(N-1,Xk。
若后者大,则输出WN,计算F(N,Xk-Wn)。
当N-1,N-2,…,到达1时,则全部输出。
(3)程序清单
read(m,n); for i:=1 to m do read(w[i],v[i]); for i:=1 to m do f[i,0]:=0; for j:=1 to n do f[0,j]:=0; for i:=1 to m do for j:=1 to n do begin f[i,j]:=f[i-1,j]; if (j>=w[i]) and (f[i,j-w[i]]+v[i]>f[i,j]) then f[i,j]:=f[i,j-w[i]]+v[i]; end; for i:=1 to m do get[i]:=0; i:=m;j:=n; while i>0 do begin if f[i,j]=f[i-1,j] then dec(i) else begin j:=j-w[i];inc(get[i]) end; end; writeln(f[m,n]); for i:=1 to m do if get[i]<>0 then writeln(i,' ',get[i]);
INPUT:
4 10
2 3 4 7
1 3 5 9
OUTPUT:
N=: 4 XK=: 10
MAX WORTH = 12
NO: 1 WEIGHT: 2 WORTH: 1 GET: 0
NO: 2 WEIGHT: 3 WORTH: 3 GET: 1
NO: 3 WEIGHT: 4 WORTH: 5 GET: 0
NO: 4 WEIGHT: 7 WORTH: 9 GET: 1
例5:四塔问题
设有A,B,C,D四个柱子(有时称塔),在A柱上有由小到大堆放的n个盘子,如图所示。

今将A柱上的盘子移动到D柱上去。可以利用B,C柱作为工作栈用,移动的规则如下:
①每次只能移动一个盘子。
②在移动的过程中,小盘子只能放到大盘子的上面。

③下面给出盘子的个数为n的一般方法,用F4(n,a,b,c,d)表示四塔问题,从A到D移动n个盘子,可以利用b,c作为工作单元,四塔问题可以分解为:
F4(n,a,b,c,d)=>F4(r,a,c,d,b)+F3(n-r,a,c,d)+ F4(r,c,a,b,d)
即如何选择r使F4(n,a,b,c,d)为最小。r的取值范围为1,2,…,n-1,为此,我们构造2个整型数组:
F3(N),F4(N),其中F3用来存放三塔问题的解。
状态转移方程为:f4
:=min{2*f4[r]+f3[n-r],1<=r<=n-1}
(3)程序清单(高精度处理)
program fourta; type arr=array[1..1000] of byte; var f4,f3:array[1..1000] of arr; w,min:arr; i,j,k,r,n:integer; function jf(a,b:arr):arr; var i,len1,len2:integer; begin i:=1000; while a[i]=0 do dec(i); len1:=i; i:=1000; while b[i]=0 do dec(i); len2:=i; if len1<len2 then len1:=len2; for i:=1 to len1 do begin a[i]:=a[i]+b[i]; a[i+1]:=a[i+1]+a[i] div 10; a[i]:=a[i] mod 10; end; jf:=a; end; function bj(a,b:arr):boolean; var i,len1,len2:integer; begin i:=1000; while a[i]=0 do dec(i); len1:=i; i:=1000; while b[i]=0 do dec(i); len2:=i; if len1<len2 then begin bj:=true;exit end; if len1>len2 then begin bj:=false;exit end; if len1=len2 then for i:=1000 downto 1 do begin if a[i]<b[i] then begin bj:=true;exit end ; if a[i]>b[i] then begin bj:=false;exit end; end; end; main begin assign(input,'fourta.in');assign(output,'fourta.out'); reset(input);rewrite(output); read(n); fillchar(w,sizeof(w),0); f3[1][1]:=1; w[1]:=1; for i:=2 to n do f3[i]:=jf(jf(f3[i-1],f3[i-1]),w); f4[1][1]:=1; for i:=2 to n do begin fillchar(min,sizeof(min),9); for j:=1 to i-1 do begin w:= jf(jf(f4[j],f4[j]),f3[i-j]); if bj(w,min) then min:=w; end; f4[i]:=min; end; i:=1000; while f4 [i]=0 do dec(i); for j:=i downto 1 do write(f4 [j]); close(input); close(output); end.
(INPUT N:10 TOTAL=49
INPUT N:1000 TOTAL=932385860354049)
例6:最小代价
(1)问题描述
设有一个N*M的方格如图所示,在方格中去掉某些点,方格边上的数字代表距离,试找出一条从A到B的路径,经过的距离和为最小(此时称为最小代价),从A前进的方向只能向右,或向下,而被去掉点的代价可看成无穷大。
(2)算法分析
采用动态规划的方法,从B向A方向推导:
当路径到达B1之后,下面仅有一条通路B1->B。而最小距离为B1B。同样,当路径到达B5之后,下面仅有一条通路B5->B,而最小距离为B5B,但当路径达到B3时,有2条通路,B3B1,B1B,或B3B5,B5B,而最小路径为min{B3B+B1最小路径,B3B5+B5最小路径}。通常在方格中某个坐标点(i,i),其最小路径为:
min{(I,J)-(I,J+1)+(I,J+1)最小路径,(I,J)->(I+1,J)+(I+1,J)的最小路径}。为了记录求出的路径,用数组D(N,M,2)来记录,其中:
D(I,J,1)表示最小路径,D(I,J,2)表示下达的方向,1—-向右,2—-向下。
而约定D(N,M,1)=0,D(N,M,2)=0。



(3)程序清单
program min_cost;
TYPE tmap=array[1..50,1..50] of integer;
tmake=array[1..50,1..50] of word;
var n,m,I,j:byte;
a:tmap;
d:tmake;
PROCEDURE MAKE;
VAR i, j : BYTE;
BEGIN
fillchar(d[n,m],sizeof(d[n,m]),0);
for i:=n-1 downto 1 do
begin d[I,m,1]:=d[i+1,m,1]+a[I,m];
d[I,m,2]:=2
end;
for j:=m-1 downto 1 do
begin d[n,j,1]:=d[n,j+1,1]+a[n,j];
d[n,j,2]:=1;
end;
for i:=n-1 downt 1 do
for j:=m-1 downto 1 do
if d[i+1,j,1]<d[I,j+1,1] then
begin d[I,j,1]:=d[i+1,j,1]+a[I,j];
d[I,j,2]:=2;
end
else
begin
d[I,j,1]:=d[I,j+1,1]+a[I,j];
d[I,j,2]:=1;
end;
end;
procedure print;
var I,j:byte;
begin
i:=1;j:=1;
while (i<n) or(j<m) do
begin write(‘(‘,I:2.’,’,j:2,’)->’);
if d[I,j,2]=1 then inc(j) else inc(i);
end;
writeln(‘(‘,n:2,’,’,m:2,’)’);
writeln(‘min cost=’,d[1,1,1]);
end;
{main}
Begin
Readln(n,m);
For i:=1 to n do
For j:=1 to m do
Begin
Read(a[I,j]);
If a[I,j]=0 then a[I,j]:=maxint;
End;
Make;
Print;
End.INPUT:
4 4
10 3 4 7
1 11 0 2
5 5 8 4
0 6 6 5
OUTPUT:
(1,1)–>(1,2)–>(1,3)–>(1,4)–>(2,4)–>(3,4)–>(4,4)
MIN COST = 30
二、练习题
1、扫雷
在一条河堤上有若干个地雷坑,每个地雷坑中埋有一定数量的地雷,地雷坑的编号为1,2,3,……,n(n<=100),如图(n=10)
地雷坑号 1 2 3 4 5 6 7 8 9 10
地雷数量 8 14 2 17 33 26 15 17 19 16
同时在每个地雷坑中都有一张说明书(除最后一个地雷除外),说明书指出,在挖完此坑的地雷后,还可以继续挖哪些坑。
挖地雷的规则是可以从任何一个地雷坑开始,到任何一个地雷坑结束,同时,在挖完某个地雷坑中的地雷后,可以选择它后面可继续挖的地雷坑这一继续挖,但只能选择一种。
问题:当地雷坑中的地雷数及后继关系给定后,找出一个挖地雷的方法,能挖到最多的地雷。(先给出状态转移方程,再写程序)
2、机器分配(HNOI’95)
总公司拥有高效生产设备M台,准备分给下属的N个公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M《=15,N〈=10。分配原则:每个公司有权获得任意数目的设备,但总台数不得超过总设备数M。保存数据的文件名从键盘输入。
数据文件格式为:第一行保存两个数,第一个数是设备台数M,第二个数是分公司数N。接下来是一个M*N的矩阵,表明了第I个公司分配J台机器的盈利。
(先给出状态转移方程,再写程序)
相关文章推荐
- C++动态规划之最长公子序列实例
- C++动态规划之背包问题解决方法
- C#使用动态规划解决0-1背包问题实例分析
- 动态规划
- C++ 动态规划
- DP(动态规划) 解游轮费用问题
- 动态规划的用法——01背包问题
- 动态规划的用法——01背包问题
- 《收集苹果》 动态规划入门
- 《DNA比对》蓝桥杯复赛试题
- 《背包问题》 动态规划
- 初学ACM - 半数集(Half Set)问题 NOJ 1010 / FOJ 1207
- 关于爬楼梯的动态规划算法
- 动态规划 --- hdu 1003 **
- DP问题各种模型的状态转移方程
- 0-1背包解题过程
- 背包问题
- USACO 3.2.2:Stringsobits
- 字符串编辑距离
- HDU ACM Step 2.2.2 Joseph(约瑟夫环问题)
