您的位置：首页 > 其它

ACM里的反素数问题

2015-10-05 22:48 465 查看

定义

对于正整数 x ，其约数的个数记做 g(x) 。例如 g(1) = 1，g(6) = 4.

如果某个正整数x满足：

对于任意 i(0<i<x) , 都有 g(i)<g(x) , 则称x为反素数·

反素数的前20项是：

1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560

对应的 g(n) 是：

1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32, 36, 40, 48, 60, 64

应用

相关问题1.

给定一个数 n，求一个最小的正整数，使得的约数个数为 n

例：codeforce 27E

思路：

由算术基本定理定理我们知道：

若一个数 x=pa11pa22⋯pass ，

那么 n 的约数个数 g(x)=(a1+1)(a2+1)⋯(as+1)

例如：12=22∗3

图片来自 acdreamer大神



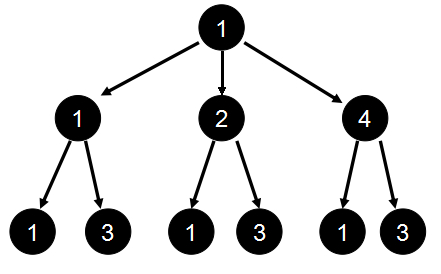
这棵树除了第一层外，每一层对应着一个素数，从上到下递增；每一层的每一个节点对应着素数的幂，从左到右递增，每一条从根节点到叶节点的路径上数字相乘即为一个约数。

我们要想获得 g(x)=n 的最小正整数，就要求x的质因子尽可能小，且尽可能多，换而言之就是幂次尽可能为1，所以就要对上面的树进行从上到下从左到右的dfs直到约数个数满足 n 。

代码：

#include<iostream>
using namespace std;
typedef unsigned long long lint;

int p[] = { 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 } ;
const lint inf = 1e18 + 5 ;
lint ans ;
int n ;

void dfs( int dept , lint tmp , int num ){
if( num > n ) return ;
if( num == n && ans > tmp ) ans = tmp ;
for( int i = 1 ; i <= 63 ; i++ ){
if( ans / p[dept] < tmp ) break ;
tmp *= p[dept] ;
dfs( dept + 1 , tmp , num*(i+1) ) ;
}
}
int main(){
while( cin >> n ){
ans = inf ;
dfs( 0 , 1 , 1 ) ;
cout << ans << endl ;
}
return 0;
}


当然也可以进行一些剪枝，不过这题没什么影响：

#include<iostream>
using namespace std;
typedef unsigned long long lint;

int p[] = { 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 } ;
const lint inf = 1e18 + 5 ;
lint ans ;
int n ;

void dfs( int dept , int limit , lint tmp , int num ){
if( num > n ) return ;
if( num == n && ans > tmp ) ans = tmp ;
for( int i = 1 ; i <= limit ; i++ ){
double t = (double)tmp ;
if ( t * p[dept] > ans ) break ;
tmp *= p[dept] ;
if ( n % ( num * ( i + 1 ) ) == 0 )
dfs( dept + 1 , i , tmp , num * ( i + 1 ) ) ;
}
}
int main(){
while( cin >> n ){
ans = inf ;
dfs( 0 , 63 , 1 , 1 ) ;
cout << ans << endl ;
}
return 0;
}


相关问题2.

给定一个数 n，求[1,n]内约数个数最多的且数值最小的数，以及其约数个数。

例：URAL 1748 ，ZOJ 2562

思路：

依然是dfs，之前是搜索到的约数个数等于题目要求时停止，现在改为搜索到的最大值比n大时停止，动态维护最大约数个数与有最大约数个数的最小值。

代码：

这里就只贴URAL 1748了（ZOJ 2562 改改即可）

#include<iostream>
using namespace std;
typedef unsigned long long lint;
int p[] = { 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 } ;
const lint inf = 1e18 + 5 ;
lint ans , n ;
int cnt ;

void dfs( int dept , int limit , lint tmp , int num )
{
if ( tmp > n ) return ;
if ( num > cnt ) {
cnt = num ;
ans = tmp ;
}
if ( num == cnt && ans > tmp ) ans = tmp ;
for ( int i = 1 ; i <= limit ; i++ ) {
if ( n < (double)tmp * p[dept] ) break ;
tmp *= p[dept] ;
dfs( dept + 1 , i , tmp , num * (i+1) ) ;
}
}

int main()
{
int t ; cin >> t ;
while ( t-- ) {
cin >> n ;
ans = inf , cnt = 0 ;
dfs( 0 , 63 , 1 , 1 ) ;
cout << ans << ' ' << cnt << endl ;
}
return 0;
}


相关问题3.

给定两个数 L,R，求[L,R]内约数个数最多的且数值最小的数，以及其约数个数。

例：HDU 2521

思路：

这题其实是个水题。。因为数据范围实在太小了，暴力即可，但找不到相关例题就用这个试了一下自己的算法。

我的想法是根据问题2里的算法求出[1,R]的约数个数最多的且数值最小的数x，然后判断这个数在不在[L,R]里面，如果不在的话再对[L,R]进行暴力。因为 x 很靠近 R，如果不在区间内说明L与R很靠近，可以直接暴力。

这个算法写出来的程序即使是长度超过10^9的区间也很快。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<string>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#include<ctime>
using namespace std;
#define clr( x , y ) memset(x,y,sizeof(x))
#define cls( x ) memset(x,0,sizeof(x))
#define pr( x ) cout << #x << " = " << x << endl
#define pri( x ) cout << #x << " = " << x << " "
#define test( t ) int t ; cin >> t ; int kase = 1 ; while( t-- )
#define out( kase ) printf( "Case %d: " , kase++ )
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
typedef long long lint;
typedef long long ll;
typedef long long LL;

int l , r ;
int ans , best ;
const int inf = 0x3f3f3f3f ;
int p[] = { 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,57 } ;

void dfs( int dept , int lim , lint tmp , int num )
{
if ( tmp > r ) return ;
if ( best < num ) {
best = num ;
ans = tmp ;
}
if ( num == best && ans > tmp ) ans = tmp ;
for ( int i = 1 ; i <= lim ; i++ ) {
if ( tmp * p[dept] > r ) break ;
dfs( dept + 1 , i , tmp *= p[dept] , num * ( i + 1 ) ) ;
}
}

int pf[100][2] ;
int getFac( int n )
{
cls( pf ) ; int k = 0 ;
for ( int i = 2 ; i * i <= n ; i++ ) {
if ( n % i == 0 ) {
pf[k][0] = i ;
while ( n % i == 0 ) {
pf[k][1] ++ ;
n /= i ;
}
k++ ;
}
}
if ( n > 1 ) {
pf[k][0] = n ;
pf[k++][1] = 1 ;
}
return k ;
}
int get( int x )
{
int len = getFac( x ) ;
int res = 1 ;
for ( int i = 0 ; i < len ; i++ ) {
res *= ( pf[i][1] + 1 ) ;
}
return res ;
}
int find( int L , int R )
{
int res = l , tmp = 0 ;
for ( int i = L ; i <= R ; i++ ) {
int num = get( i ) ;
if ( num > tmp ) {
tmp = num ;
res = i ;
}
}
return res ;
}
void work()
{
ans = inf , best = 0 ;
dfs( 0 , 63 , 1 , 1 ) ;
if ( l <= ans && ans <= r )
cout << ans << endl ;
else
cout << find( l , r ) << endl ;
}
int main()
{
int t ; cin >> t ;
while ( t-- ) {
cin >> l >> r ;
work() ;
}
return 0;
}


相关问题4.

给定一个数k，求出一个最小正整数X，满足X的约数个数为X-K。

例：HDU 4542

思路：

HDU 4542的具体题意是这样的：

给出一个数K和操作类型Type：

若 Type == 0，求出一个最小正整数X，满足X的约数个数为K。

若 Type == 1，求出一个最小正整数X，满足X的约数个数为X-K。

对于 Type == 0 ，用问题1的算法直接搞即可，但这题TMD只给了200ms，必须用第二个经过剪枝的算法。

对于 Type == 1 ，可以这么想：对于一个数 n ，它有 x 个约数，k 个非约数，显然 n = x + k ，n 的约数个数为 x 废话。

那么对于给定的 k ，我们只要从2开始升序枚举约数个数 x ，使 x + k 的约数个数为 x 即是答案，又因为一个数的约数最多只有 2(√x+k) 个，如果枚举到 2(√x+k) 依然无答案则输出”Illgeal” 。

当然也有一种方法来直接预处理出非约数个数对应的值，因为非约数个数 k 对应的值 x 很接近 k，所以直接两层循环搞也是可以的：

void Init(){
for ( int i = 1 ; i <= 50000 ; i++ ) findx[i] = i;
for ( int i = 1 ; i <= 50000 ; i++ ) {
for ( int j = i ; j <= 50000 ; j += i) findx[j]--;
if ( !findx[findx[i]] ) findx[findx[i]] = i;
findx[i] = 0;
}
}


代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<string>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<stack>
#include<bitset>
#include<ctime>
using namespace std;
#define clr( x , y ) memset(x,y,sizeof(x))
#define cls( x ) memset(x,0,sizeof(x))
#define pr( x ) cout << #x << " = " << x << endl
#define pri( x ) cout << #x << " = " << x << " "
#define test( t ) int t ; cin >> t ; int kase = 1 ; while( t-- )
#define out( kase ) printf( "Case %d: " , kase++ )
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
typedef unsigned long long lint;
typedef long long ll;
typedef long long LL;

int type , k ;
const lint inf = ( 1LL << 63 ) ;
const int N = 50000 ;
lint ans ;
int pf[100][2] ;
bool noprime[N+5] ;
vector<int>p ;
int getPri()
{
cls( noprime ) ;
int m = (int)sqrt( N + 0.5 ) ;
for ( int i = 2 ; i <= m ; i++ )
{
if ( !noprime[i] )
for ( int j = i * i ; j <= N ; j += i )
noprime[j] = true ;
}
for ( int i = 2 ; i <= N ; i++ )
if ( !noprime[i] ) p.pb(i) ;
return p.size() ;
}
int getFac( int n )
{
cls( pf ) ; int k = 0 ;
for ( int i = 0 ; p[i] * p[i] <= n ; i++ )
{
if ( n % p[i] == 0 )
{
pf[k][0] = p[i] ;
while ( n % p[i] == 0 )
{
pf[k][1] ++ ;
n /= p[i] ;
}
k++ ;
}
}
if ( n > 1 )
{
pf[k][0] = n ;
pf[k++][1] = 1 ;
}
return k ;
}
void dfs( int dept , int lim , lint tmp , int num )
{
if ( num > k ) return ;
if ( num == k && ans > tmp ) ans = tmp ;
for ( int i = 1 ; i <= lim ; i++ )
{
if ( ans / p[dept] < tmp ) break ;
tmp *= p[dept] ;
if ( k % ( num * ( i + 1 ) ) == 0 )
dfs( dept + 1 , i , tmp , num * ( i + 1 ) ) ;
}
}

int get( int x )
{
int len = getFac( x ) ;
int res = 1 ;
for ( int i = 0 ; i < len ; i++ )
res *= ( pf[i][1] + 1 ) ;
return res ;
}
void work()
{
if ( !type )
{
ans = inf ;
dfs( 0 , 62 , 1 , 1 ) ;
if ( ans > ( 1LL << 62 ) )
puts( "INF" ) ;
else
cout << ans << endl ;
}
else
{
int tmp = 2 ;
while ( tmp * tmp <= 4 * ( tmp + k ) )
{
if ( tmp == get( tmp + k ) )
{
cout << tmp + k << endl ;
return ;
}
tmp ++ ;
}
puts( "Illegal" ) ;
}
}
int main()
{
getPri() ;
test(t)
{
scanf( "%d%d" , &type , &k ) ;
out( kase ) ;
work() ;
}
return 0;
}
内容来自用户分享和网络整理，不保证内容的准确性，如有侵权内容，可联系管理员处理 点击这里给我发消息
标签：  反素数 数论
相关文章推荐
新的分享
章节导航